Strukturgleichungsmodelle

Allgemeine Einführung

Bei einer Untersuchung empirischer Sachverhalte suchen Psychologen, Biologen, Statistiker etc. nach Zusammenhängen zwischen verschiedenen Größen. Dabei kann man diese Variablen sowohl durch messbare (beobachtbare) als auch durch latente (unbeobachtbare) Variablen modellieren. Eine oft verwendete Methode stellt dabei die lineare Regression dar. Mit dieser Methode erfasst Du den linearen Zusammenhang der untersuchten messbaren Variablen. Du bekommst dabei aber keine Information über die Ursache-Wirkung (Kausalität) zwischen Deinen Variablen. Außerdem können die komplexen Zusammenhänge Deiner Variablen unentdeckt bleiben.

Das Strukturgleichungsmodell kann diese beiden Punkte lösen. Insbesondere kann es Dir ein einen Einblick in die „verborgenen“ Strukturen Deiner Variablen geben (daher der Name). Es handelt sich bei dem Verfahren um eine Mischung aus der Faktoranalyse, der linearen Regression und der Pfadanalyse. In der Literatur wird der Begriff „Strukturgleichungsmodell“ für verschiedene, aber im Kern ähnliche Verfahren verwendet. Wie bei den meisten statistischen Analyseverfahren, musst Du auch Hypothesen bilden und diese dann auf Signifikanz testen. Die Faktorenanalyse kannst Du dabei auch zur Definition latenter Variablen verwenden.

Ein Strukturgleichungsmodell in der Praxis

Angenommen Du stellst die folgende Hypothese auf:

Stress und harte körperliche Arbeit verschlechtern den Gesundheitszustand.

Wie Du siehst, handelt es sich dabei um einen kausalen Zusammenhang zwischen den exogenen latenten Variablen Stress und körperliche Arbeit sowie der endogenen, latenten Variable Gesundheitszustand. Mit Hilfe eines Strukturgleichungsmodells kannst Du nach der Struktur im Zusammenhang Deiner Variablen suchen. Hierfür brauchst Du messbare Variablen, um die latenten Variablen zu erfassen. In diesem Beispiel kannst Du Stress beispielsweise durch Schlafenszeiten und Gewichtabnahme messen. Die körperliche Arbeit kannst Du durch die verbrannten Kalorien und Erschöpfungsfälle messen. Den Gesundheitszustand kannst Du z.B. durch den Blutzuckerspiegel und den Blutdruck messen. Damit Du den Überblick über Dein Modell behältst, ist eine grafische Darstellung in Form eines Pfaddiagramms sehr hilfreich. Das folgende Pfaddiagramm stellt das

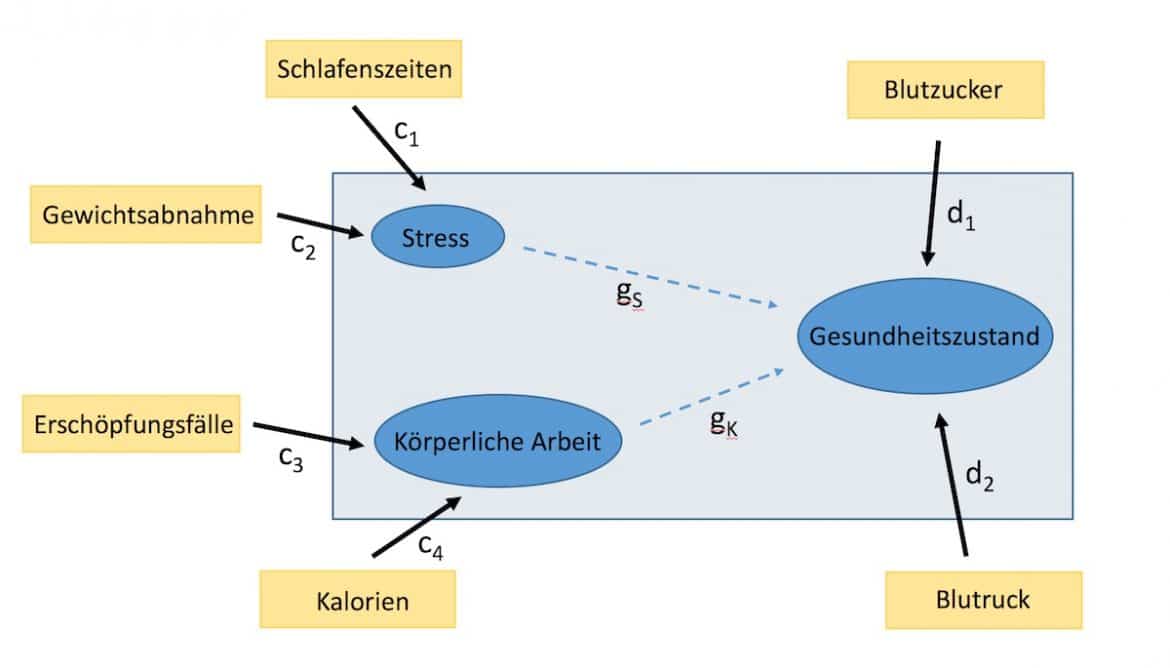
Eine graphische Darstellung des Modells aus dem obigen Beispiel mit Hilfe eines Pfaddiagramms.

Strukturgleichungsmodell des obigen Beispiels dar. Die messbaren Variablen erkennst Du als gelbe Vierecke und die latenten Variablen als blaue Ovale. Das Strukturmodell ist umrandet. Die gestrichelten Pfeile stellen die Dich interessierende Struktur dar. Deine Hypothese lautet mathematisch:

Die Modellparameter und sind signifikant von 0 verschieden.

Die Parameter bis sowie und sind die messbaren Parameter, und können z.B. über die Faktorenanalyse bestimmt werden. Nach Bestimmung der Parameter kannst Du das Pfaddiagramm dementsprechend aktualisieren. Alternativ zur obigen Hypothese kannst Du die latenten Variablen, also die Struktur des Modells, mit Hilfe von der Faktor- bzw. der Varianzanalyse abschätzen.

Wie schätzt man die Parameter?

Am folgenden Beispiel siehst Du gut, wie die latenten Variablen bestimmt und die Parameter geschätzt werden. In der unteren Abbildung findest Du ein Streudiagramm von zwei fiktiven Datensätzen für Schlafzeiten und Gewichtabnahmen mit jeweils 200 Werten. Die Zeitreihen wurden jeweils um 0 zentriert (durch Abzug des Mittelwerts der Werte von jedem Wert). Um beim obigen Beispiel zu bleiben, ist die latente Variable Stress mit Hilfe der Faktoranalyse zu bestimmen. Wie Du in der Abbildung sehen kannst, ist die Datenstreuung, also die Datenvarianz, entlang verschiedener

Variable	Parameter	Wert
Schlafenszeiten	c1	0,3
Gewichtsabnahme	c2	0,7

Tabelle 1: Datenvarianz

 

Variable	Varianz
X1	0,97
X2	4,88
X1′	5,71
X2′	0,15

Tabelle 2: Parameter zur Faktorbestimmung

Ursprunggeraden unterschiedlich groß. Du willst nun die Varianz der Variable Stress mit Deinen messbaren Variablen maximal erklären und suchst dementsprechend nach der Richtung mit der maximalen Varianz. Das kannst Du mit mehreren Methoden machen.

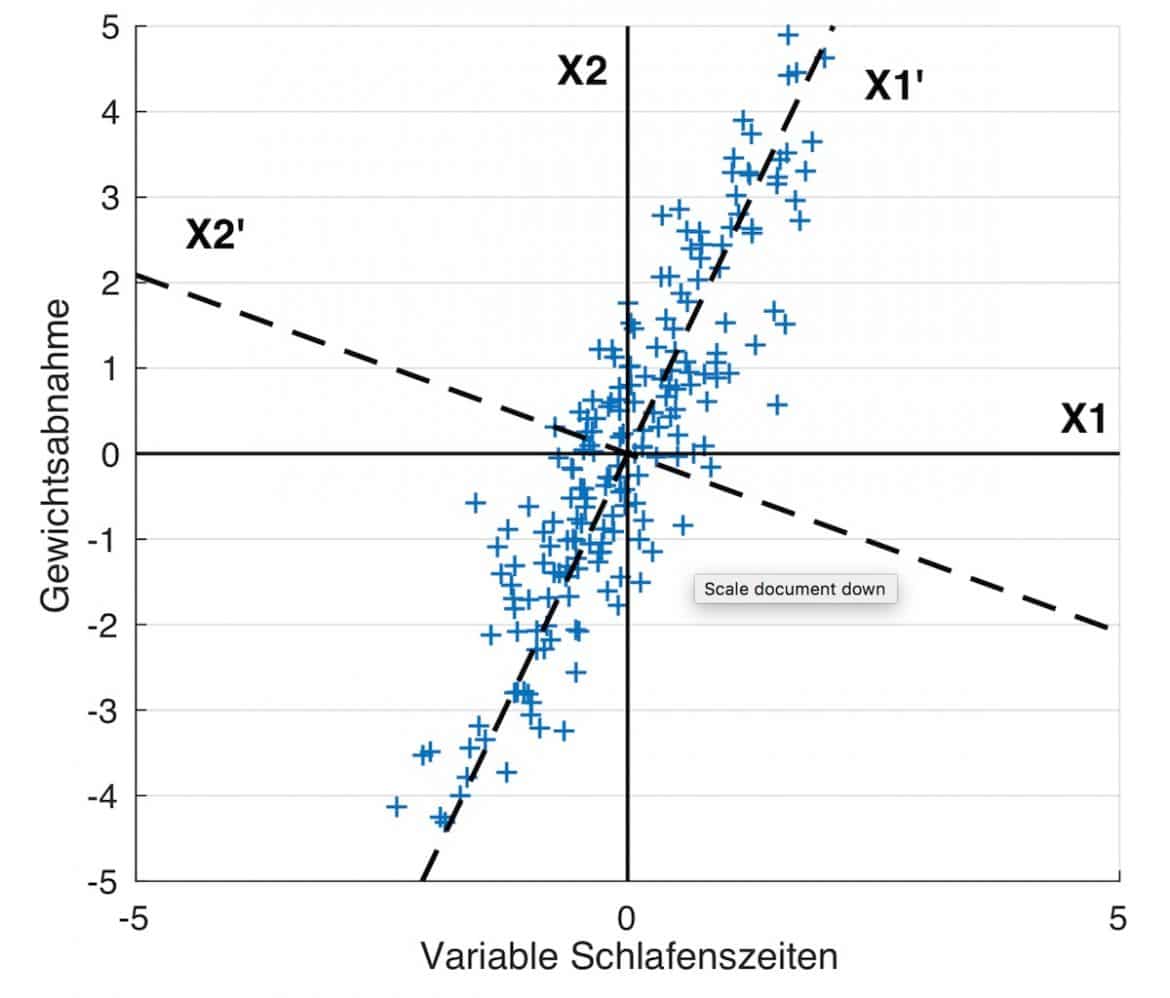
Eine gute und oft verwendete Methode ist die Hauptachsen-Methode (vgl. Hauptkomponentenanalyse). Diese Methode bestimmt die Ursprungsgerade, also die erste Hauptachse, entlang derer Datenstreuung maximal ist. Damit kannst Du dann die zweite Hauptachse bestimmen. Diese hat die größte Datenvarianz unter allen Ursprungsgeraden, die zur ersten Hauptachse senkrecht sind. Ähnlich gehst Du bei der Bestimmung weiterer Hauptachsen vor. Die Methode kannst Du Dir als Änderung des gesamten Koordinatensystems vorstellen.

Für die vorliegenden Daten sind die zwei Hauptkomponenten als die zwei durchgestrichene Linien X1’ und X2’ in der Abbildung dargestellt. Die Datenvarianzen kannst du der Tabelle 1 entnehmen. Die Varianz entlang der ursprünglichen Koordinaten (durchgezogen X1 und X2) ist kleiner als die Varianz entlang der ersten Hauptachse X1’ und größer als die Varianz entlang der zweiten Hauptachse X2’. Diese neue Variable X1’ kannst Du dann als Deinen Faktor 1, also die latente Variable Stress ansehen.

Mit dieser Methode bekommst Du nicht nur die Varianzen, sondern auch die Parameter und heraus. Die Ergebnisse hierfür kannst du der Tabelle 2 entnehmen. Die durch die messbaren Variablen erklärten Werte der latenten Variablen Stress berechnest Du mit der folgenden Gleichung (abgekürzte Variablennamen):

   

Somit erklärst Du die Datenvarianz entlang der ersten Hauptkomponente X1’ von 5,71. Die Varianz entlang der zweiten Hauptkomponente X2’ von 0,15 ist die unerklärte Varianz, die 2,6% von der erklärten Varianz beträgt.

Nachdem Du so alle Deine latenten Variablen bestimmt hast, kannst Du die Parameter und beispielsweise mit linearer Regression schätzen. Die entsprechende Gleichung lautet, wobei für die körperliche Arbeit steht:

   

In dieser Gleichung ist die nicht durch die Variablen in der Gleichung erklärte Varianz der Variable Gesundheit. Die Regressionsparameter , und kannst Du am einfachsten mit Hilfe einer statistischen Software bestimmen. Die meisten Programme liefern sowohl die geschätzten Werte als auch die Signifikanz der Schätzung. In der unteren Tabelle findest Du eine Beispielschätzung für fiktive Datenwerte. So könnte beispielsweise der Output aussehen:

Variable	Geschätzter Wert	t-Statistic	p-Wert
Konstante	0,04	0,59	0,55543
Stress	0,89	12,26	4,10E-25
KArbeit	-0,64	-9,30	2,78E-13

Beim Signifikanz-Test der Regressionskoeffizienten berechnet das Programm, ob geschätzte Modellparameter (zweite Spalte) einen signifikanten Beitrag zum Modell liefern. Die Nullhypothese besagt, dass die Modellparameter alle sind und die Berechnung liefert Aussagen darüber, ob diese Annahme pro Parameter gerechtfertigt ist oder verworfen werden kann. Diese Art von statistischem Test wird -Test genannt (vgl. 3te Spalte). Wie Du der Tabelle entnehmen kannst, ist die Schätzung für den konstanten Regressionskoeffizienten nicht signifikant von verschieden, da der -Wert sehr groß ist. Für die anderen beiden Parameter ist der -Wert extrem klein, sodass man mit gutem Gewissen die Nullhypothese verwerfen kann und sagen kann, dass die Parameter einen signifikanten Einfluss auf das Modell haben. In der Regel gelten in der Statistik -Werte kleiner als 0.05 als signifikant.

Die Vorgehensweise

1. Formulierung der Fragestellung (Hypothese): Bei diesem Punkt musst Du Dir gründlich überlegen welcher konkreten Fragestellung Du nachgehen willst. Das ist der zentrale Aspekt Deines Modells, das heißt dessen Struktur.

2. Auswahl der messbaren Variablen und Pfaddiagramm: Um Deine Hypothesen empirisch zu überprüfen, musst Du die messbaren Variablen auswählen. Diese sollten sowohl Deine Hypothese bestätigen können, als auch repräsentativ sein. Anschließend stellst Du das gesamte Modell grafisch mit Hilfe eines Pfaddiagrams dar (wie oben).

3. Modellstruktur erkennen: Anhand Deines Pfaddiagramms erkennst Du die vermuteten bzw. die erwarteten Zusammenhänge. Insbesondere hast Du dadurch eine gute Übersicht, die Du bei mehreren Variablen schnell verlieren kannst.

4. Schätzung der Parameter und Test auf Signifikanz: Die Schätzungen der Parameter im Strukturgleichungsmodell können variieren. Die gängigsten Methoden sind die lineare Regression und die Faktoranalyse bzw die Hauptkomponentenanalyse, wie Du im obigen Beispiel sehen konntest. In der Praxis verwendet man hierzu Programme, die alle notwendigen Schritte zur Berechnung vornehmen. Wichtige Software-Pakete hierfür sind beispielsweise SPSS Amos, Mplus oder SmartPLS.

5. Mögliche Änderungen im Modell: Du kannst die Parameter, die nicht signifikant von 0 verschieden sind, verwerfen. Die entsprechenden Pfeile im Pfaddiagramm entfernst Du dann. Dabei sollten die nicht signifikanten Parameter nur einmal verworfen werden. Mit dem Blick auf das aktualisierte Pfaddiagramm kannst Du die Schätzung noch einmal ohne die verworfenen Parameter durchführen. Abhängig vom Endergebnis kannst Du Deine Hypothese verwerfen, beibehalten oder auch neu interpretieren.

Literatur

Jöreskog, K. G. & Sörbom, D. (1989). LISREL 7: A guide to the program and applications (2nd ed.). Chicago, IL: SPSS