Student-Verteilung (t-Verteilung)

Student-Verteilung (t-Verteilung)

  • 16. April 2018
  • Posted by: Mika
Keine Kommentare

Die t-Verteilung ist zum Durchführen von Testverfahren konstruiert, ist also eine Testverteilung. Du verwendest sie beispielsweise beim Test auf Mitte einer normalverteilten Zufallsvariable, wenn Deine Stichprobe klein und die Varianz nicht bekannt ist. Man spricht dann auch vom t-Test.

Stell Dir beispielsweise vor, Dir liegen Beobachtungswerte von unabhängig identisch normalverteilten Zufallsvariablen X_1, … X_n vor. Anhand dieser Stichproben möchtest Du dann testen, ob Deine Beobachtungen mit der Annahme eines angegebenen Mittelwerts vereinbar ist.

Dazu nimmst Du als Prüfgröße die Differenz d zwischen dem Stichproben- und dem angegebenen Mittelwert und standardisierst sie.

Prüfung mittels Gauß-Test

Falls Du die Varianz \sigma^2 der Grundgesamtheit kennst, ist das Vorgehen einfach: Du erhältst eine standardnormalverteilte Prüfgröße, die Du im Gauß-Test mit dem passenden kritischen Wert vergleichen kannst.

    \begin{equation*} \sigma^2 \nobreakspace bekannt: \quad z=\frac {d} {\sigma / \sqrt n} \sim N(0;1)-verteilt \end{equation*}

Kennst Du die Varianz der Grundgesamtheit nicht, musst Du sie also aus den Stichprobenrealisationen mit der Schätzfunktionen

    \begin{equation*} \hat \sigma^2 = S_X^2 = \frac 1 {n-1} \cdot \sum_{i=1}^n(X_i-\bar X)^2 \end{equation*}

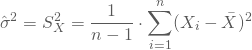
schätzen, so gilt diese Verteilungsannahme dagegen nicht.

Gosset veröffentlichte 1908 unter dem Pseudonym Student die t-Verteilung, der die Prüfgröße im Fall von unbekannter Varianz folgt.

Wie sieht die t-Verteilung aus?

Seine Verteilung ist die Verteilung des Quotienten aus einer standardnormalverteilten Zufallsvariablen Z und der Wurzel aus einer Chi-Quadrat-verteilten Zufallsvariablen W, außerdem dividiert durch deren Freiheitsgrade \nu=(n-1). W ist also die Quadratsumme von n standardnormalverteilten Zufallsvariablen Z_i ist.

    \begin{equation*} T = \frac Z {\sqrt {W/\nu}} = \frac Z {\sqrt W} \cdot \sqrt {\nu} \quad und \quad W = \sum_{i=1}^n Z_i^2 \end{equation*}

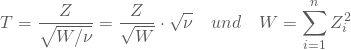
Diese (zusammengesetzte) Zufallsvariable besitzt äußert komplizierte Dichte- und Verteilungsfunktionen, die aber bequem tabelliert vorliegen, in Abhängigkeit von den Freiheitsgraden \nu = (n-1).

Es gilt

    \begin{equation*} E(T) = 0 \quad und \quad Var(T) = \frac n {n-2} \end{equation*}

Nun folgt der Quotient aus \nu \cdot S_X^2 und der tatsächlichen Varianz einer Chi-Quadrat-Verteilung mit \nu=(n-1) Freiheitsgraden:

    \begin{equation*} \frac {\nu \cdot S^2} {\sigma^2} = \frac {\displaystyle\sum_{i=1}^n(X_i-\bar X)^2} {\displaystyle\sigma^2} = \displaystyle\sum_{i=1}^n \left( \frac {X_i-\bar X} { \sigma}\right)^2 \quad \sim \quad \chi^2_{(n-1)}-verteilt \end{equation*}

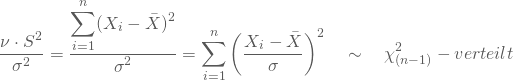
und die mit der unbekannten Varianz standardisierte Differenz z=\frac {d} {\sigma / \sqrt n} ist standardnormalverteilt. Damit folgt der Quotient

    \begin{equation*} t= \frac d {S / \sqrt {n}} = \frac d {\sigma /\sqrt n} \cdot \frac {\sigma}{S} \quad \sim \quad t_{n-1}-verteilt \end{equation*}

einer t-Verteilung mit \nu=(n-1) Freiheitsgraden.

Schätzung mittels t-Test

Du kannst Deinen obigen Test auf Mitte daher ähnlich einfach wie den Gauß-Test durchführen, indem Du Deine mit der Stichprobenvarianz standardisierte Differenz mit dem passenden kritischen Wert der t-Verteilung mit \nu=(n-1) Freiheitsgraden vergleichst.

Je größer die Anzahl der Freiheitsgrade, desto sicherer wird die Schätzung der Varianz und desto stärker nähert sich die t-Verteilung an die Standardnormalverteilung an. Die linke Grafik zeigt die Dichtefunktionen der t-Verteilung in Abhängigkeit von ihren Freiheitsgraden, die rechte Grafik enthält die zugehörigen Verteilungsfunktionen.

Student-Verteilung (t-Verteilung)

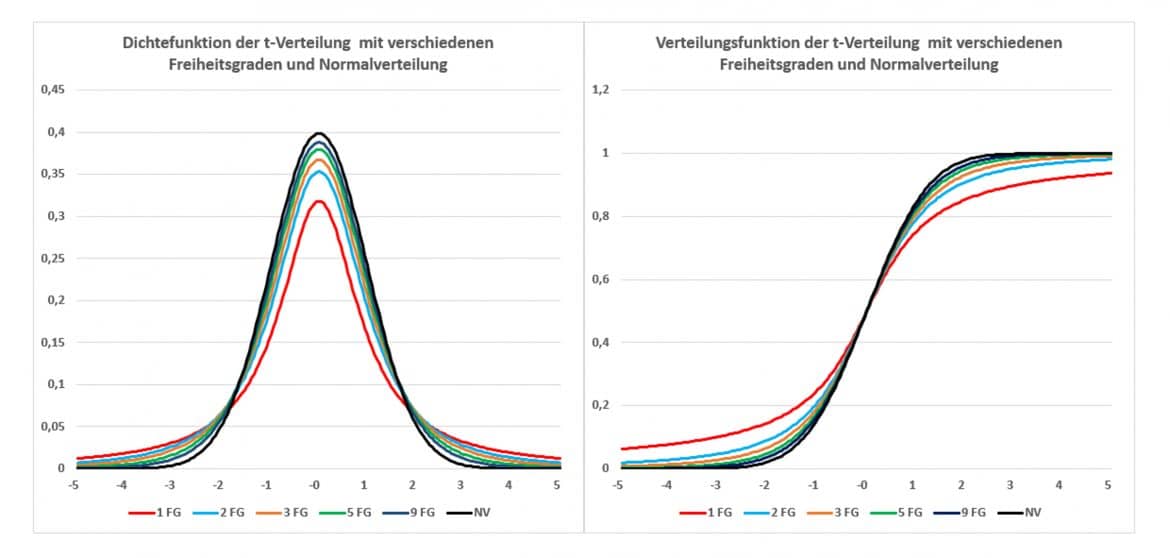
Die t-Verteilung nähert sich mit zunehmendem Stichprobenumfang asymptotisch an die Standardnormalverteilung an und Du kannst sie ab n=100 approximieren.