Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Fisher-Verteilung (F-Verteilung)
- 16. April 2018
- Posted by: Mika
Als Testverteilung, d.h. als Verteilung, die nicht eine im Experiment beobachtbare Zufallsvariable beschreibt, sondern eine, die zu Testzwecken konstruiert wurde, beschreibt die F-Verteilung den Quotienten zweier ![]() -verteilter Zufallsvariablen, jeweils dividiert durch die Anzahl ihrer Freiheitsgrade.
-verteilter Zufallsvariablen, jeweils dividiert durch die Anzahl ihrer Freiheitsgrade.
Wofür verwendet man die F-Verteilung?
Du verwendest sie hauptsächlich zum Varianzvergleich zweier Stichproben aus normalverteilten Grundgesamtheiten und außerdem für die Varianzanalyse zum Vergleich auf signifikante Unterschiede bei den Stichprobenmitteln.
Hast Du beispielsweise n voneinander unabhängige standardnormalverteilte Zufallsvariablen ![]() , …
, … ![]() sowie m voneinander unabhängige standardnormalverteilte Zufallsvariablen
sowie m voneinander unabhängige standardnormalverteilte Zufallsvariablen ![]() , …,
, …, ![]() gegeben, so kannst Du aus den jeweiligen Quadratsummen dann zwei
gegeben, so kannst Du aus den jeweiligen Quadratsummen dann zwei ![]() -verteilte Zufallsvariablen bilden:
-verteilte Zufallsvariablen bilden:
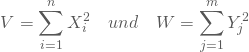
V besitzt ![]() Freiheitsgrade, W
Freiheitsgrade, W ![]() . Der Quotient aus beiden durch ihre Freiheitsgrade dividierten Zufallsvariablen ist dann F-verteilt mit
. Der Quotient aus beiden durch ihre Freiheitsgrade dividierten Zufallsvariablen ist dann F-verteilt mit ![]() Freiheitsgraden.
Freiheitsgraden.
![]()
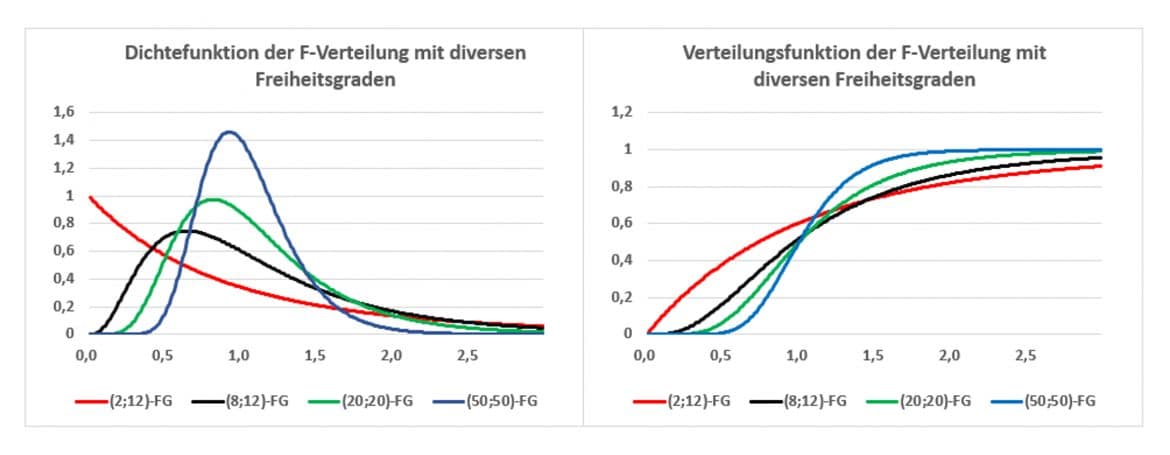
In Abhängigkeit von den beiden Freiheitsgraden sind einerseits in der linken Grafik die Dichte und andererseits in der rechten Grafik die Verteilungsfunktionen eingezeichnet:
Kennzahlen der Chi-Quadrat-Verteilung
Erwartungswert und Varianz der F-Verteilung sind
![]()
und
![]()
Beispiel für Prüfung auf Varianz-Gleichheit
Stell Dir vor, Du ziehst zum Beispiel aus zwei normalverteilten Grundgesamtheiten zwei Stichproben von unterschiedlichem Umfang und möchtest testen, ob beide die gleiche Varianz besitzen. Du möchtest etwa wissen, ob die Preisschwankungen von Flugtickets im Internet höher sind als beim Verkauf im Reisebüro.
Dazu ermittelst Du an beliebigen Tagen die Preise Deines Wunschtickets nach London mit der Fluggesellschaft FliegWeiter. Die Preise im Reisebüro beobachtest Du ferner als Realisationen von X,
| Tag | 1 | 2 | 3 | 4 | ||
| 29,99 | 35,50 | 75,00 | 55,00 | 48,87 | 418,52 |
die im Internet zudem als Realisationen von Y.
| Tag | 1 | 2 | 3 | 4 | 5 | ||
| 35,50 | 38,50 | 42,60 | 56,90 | 88,20 | 52,34 | 469,18 |
Berechnung der empirischen Varianzen
Aus beiden Stichproben berechnest Du zuerst die Stichprobenvarianzen ![]() und
und ![]() . Falls X und Y die gleiche Varianz
. Falls X und Y die gleiche Varianz ![]() in der Grundgesamtheit haben, kannst Du beide Stichprobenfunktionen für die Varianz, jeweils multipliziert mit ihren Freiheitsgraden, durch
in der Grundgesamtheit haben, kannst Du beide Stichprobenfunktionen für die Varianz, jeweils multipliziert mit ihren Freiheitsgraden, durch ![]() teilen und erhältst zwei
teilen und erhältst zwei ![]() -verteilte Zufallsvariablen:
-verteilte Zufallsvariablen:
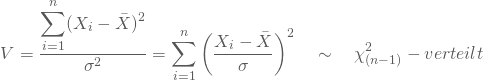
und
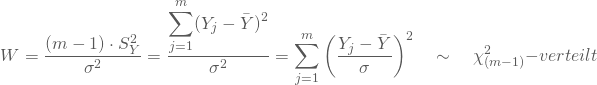
Auf dem Weg zur F-Verteilung
Teilst Du dann V und W beide durch die zugehörigen Freiheitsgrade ![]() und
und ![]() und bildest den Quotienten aus beiden, so erhältst Du eine F-verteilte Zufallsvariable:
und bildest den Quotienten aus beiden, so erhältst Du eine F-verteilte Zufallsvariable:
![]()
Die Umformung nach dem zweiten Gleichheitszeichen erfolgt schließlich durch Kürzen mit ![]() im Zähler und im Nenner.
im Zähler und im Nenner.
Die Testentscheidung
Du kannst Deine Testentscheidung fällen, indem Du den Wert Deiner Prüfgröße mit dem Wert der F-Verteilung mit ![]() Freiheitsgraden zur gegebenen Irrtumswahrscheinlichkeit vergleichst.
Freiheitsgraden zur gegebenen Irrtumswahrscheinlichkeit vergleichst.
Bei der F-Verteilung gilt die reziproke Symmetrie, d.h. es ist
![]()
Für große Stichproben kannst Du die F-Verteilung übrigens durch die Normalverteilung approximieren.
