Chi-Quadrat-Verteilung

Chi-Quadrat-Verteilung

  • 16. April 2018
  • Posted by: Mika
Keine Kommentare

Du verwendest diese Verteilung etwa für die Durchführung von Chi-Quadrat-Anpassungs-, Unabhängigkeits- oder Homogenitätstest sowie für die Konstruktion eines Konfidenzintervalls für die Varianz einer normalverteilten Zufallsvariable. Außerdem bildet sie die Grundlage für t-Verteilung und F-Verteilung.

Die Chi-Quadrat-Verteilung ist eine Testverteilung, also eine Verteilung, die konstruiert wurde, um Hypothesentests durchführen zu können. Sie ist weiterhin die Verteilung der Quadratsumme standardnormalverteilter Zufallsvariablen.

Wie sieht die Chi-Quadrat-Verteilung aus?

Hast Du n voneinander unabhängige standardnormalverteilte Zufallsvariablen X_1, … X_n gegeben und bildest dann deren Quadratsumme, so erhältst Du die Zufallsvariable W:

    \begin{equation*} W = \sum_{i=1}^n X_i^2 \end{equation*}

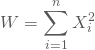
W kann wegen der Quadrierung keinen negativen Wert annehmen und die Dichtefunktion ergibt sich als:

    \begin{equation*} f(w) = \begin{cases} \frac {w^{\frac n 2 -1}\cdot e^{-\frac w 2}}{2^{\frac n 2}\cdot \Gamma(\frac n 2)}, \nobreakspace f\"ur \nobreakspace w >0 \\ \\ 0 \nobreakspace sonst \end{equation*}

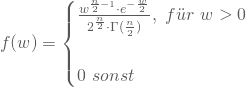
Dabei ist \Gamma(\frac 1 2)=\sqrt {\pi} und \Gamma(r+1)=r\cdot \Gamma(r), \nobreakspace f\"ur \nobreakspace r>0.

Integrierst Du über diese – zugegebenermaßen nicht einfache – Funktion, erhältst Du die Verteilungsfunktion von W, die wie viele andere Verteilungen, ebenfalls bequem tabelliert vorliegt.
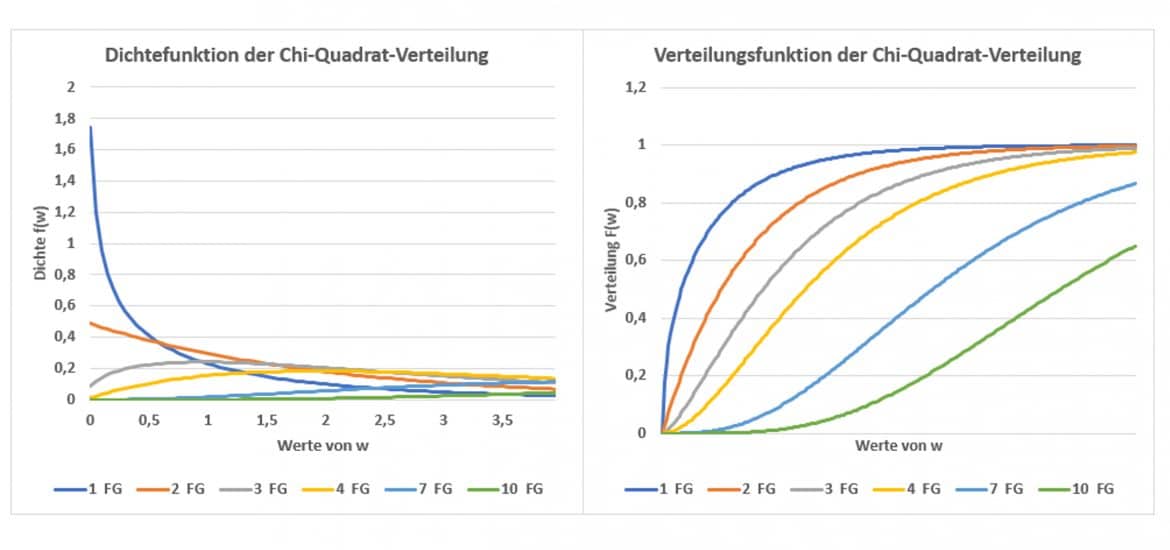
Mit zunehmender Anzahl n der Summanden in W gleichen sich extreme Werte einzelner Realisationen stärker aus. W besitzt zudem \nu=(n-1) Freiheitsgrade, den Parameter der Verteilung. Die Grafik zeigt Dichte und Verteilungsfunktion in Abhängigkeit von \nu: Je größer \nu ist, umso flacher verlaufen beide Funktionen.

Chi-Quadrat-Verteilung

Erwartungswert und Varianz der Chi-Quadrat-Verteilung hast Du durch

    \begin{equation*} E(W) = \nu \quad und \quad Var(W)=2 \nu \end{equation*}

gegeben.

Für große n, etwa ab n=50, kannst Du die Chi-Quadrat-Verteilung durch die Standardnormalverteilung approximieren, durch

    \begin{equation*} Z^* = \sqrt {2\cdot W^2} - \sqrt {2 n - 1} \end{equation*}