Weibull-Verteilung

Weibull-Verteilung

  • 16. April 2018
  • Posted by: Mika
Keine Kommentare

aDie Weibull-Verteilung ist eine stetige zweiparametrige Verteilung, die für nicht negative reelle Zahlen definiert ist und die Du zudem flexibel für die Modellierung verschiedenster Prozesse verwenden kannst.

Ein häufiger Einsatzbereich ist die Bestimmung von Wahrscheinlichkeiten für beispielsweise Lebenszeiten von Maschinen oder Bauteilen, wobei anders als bei der Exponentialverteilung Alter und Nutzungsintensität mit in die Berechnungen eingehen können. Besonders im Falle von kostenintensiven Anlagen ist diese aufwendige Differenzierung von Bedeutung.

Empirische Untersuchungen zeigen nämlich bei vielen Anlagen

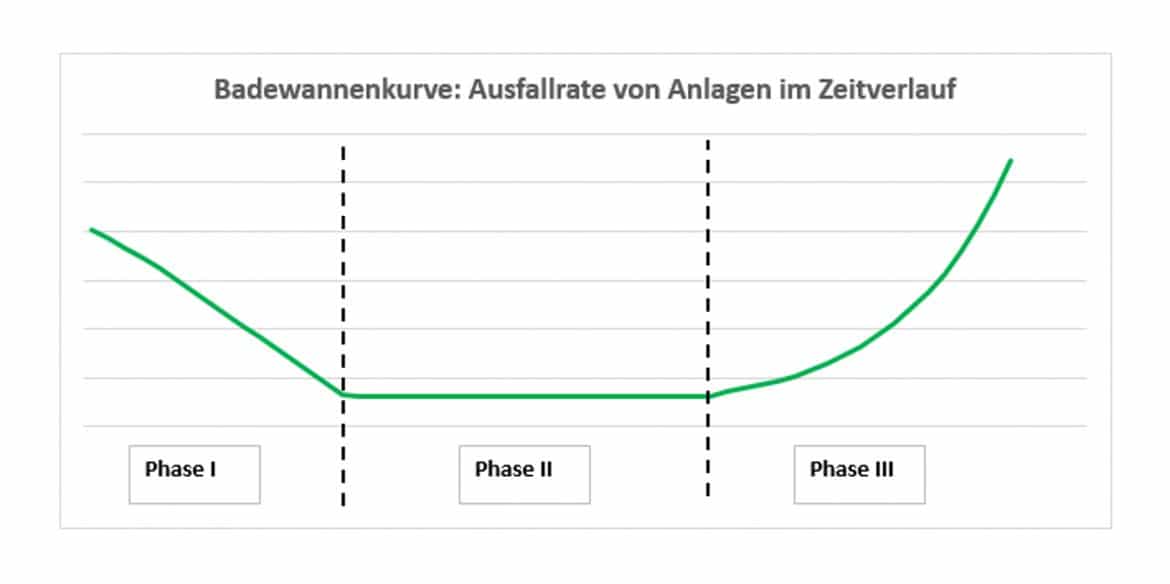
  • in der ersten Phase eine zunächst hohe, dann sinkende Ausfallwahrscheinlichkeit, etwa bis die optimale Einrichtung und Einstellung erfolgt ist,
  • in der zweiten Phase eine gleichleibend niedrige Ausfallrate und außerdem
  • mit zunehmendem Alter in der dritten Phase altersbedingt eine ansteigende Ausfallrate.

Dieser Verlauf wird als Badewannenkurve bezeichnet und ist in der Grafik dargestellt.

Weibull-Verteilung

  • Um dieser typischen Entwicklung der Ausfallrate im Zeitablauf gerecht zu werden, verwendest Du bei der Weibull-Verteilung zusätzlich zum Skalenparameter 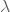\lambda den Formparameter b >0.
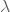    \lambda gibt zudem die mittlere Ausfallwahrscheinlichkeit pro Intervall an und berechnet sich als Kehrwert der mittleren Lebensdauer T: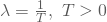 \lambda=\frac 1 T, \nobreakspace T>0
  • Den Formparameter b verwendest Du dagegen, um Veränderungen der Ausfallrate im Zeitablauf modellieren zu können:
    für b=1 erhältst Du die Exponentialverteilung mit der Voraussetzung einer konstanten Ausfallwahrscheinlichkeit,

    • b<1 bedeutet abnehmende und
    • b>1 zunehmende Ausfallraten.

Charakterisierung der Weibull-Verteilung

Die Dichtefunktion der Weibull-Verteilung ist mit

    \begin{equation*} f(x;\lambda,b)=\lambda \cdot b \cdot (\lambda \cdot x) ^{(b-1)}\cdot e^{-(\lambda \cdot x)^b} \end{equation*}

gegeben, ihre Verteilungsfunktion mit

    \begin{equation*} F(x;\lambda,b)=1 - e^{-(\lambda \cdot x)^b} \end{equation*}

Die Verteilungsfunktion gibt Dir die Wahrscheinlichkeit an, mit der die Anlage spätestens bis x ausgefallen ist. Entsprechend kannst Du die Wahrscheinlichkeit, mit der die Maschine in x noch lebt, als

    \begin{equation*} G(x)=1 - F(x) = e^{-(\lambda \cdot x)^b} \end{equation*}

darstellen.

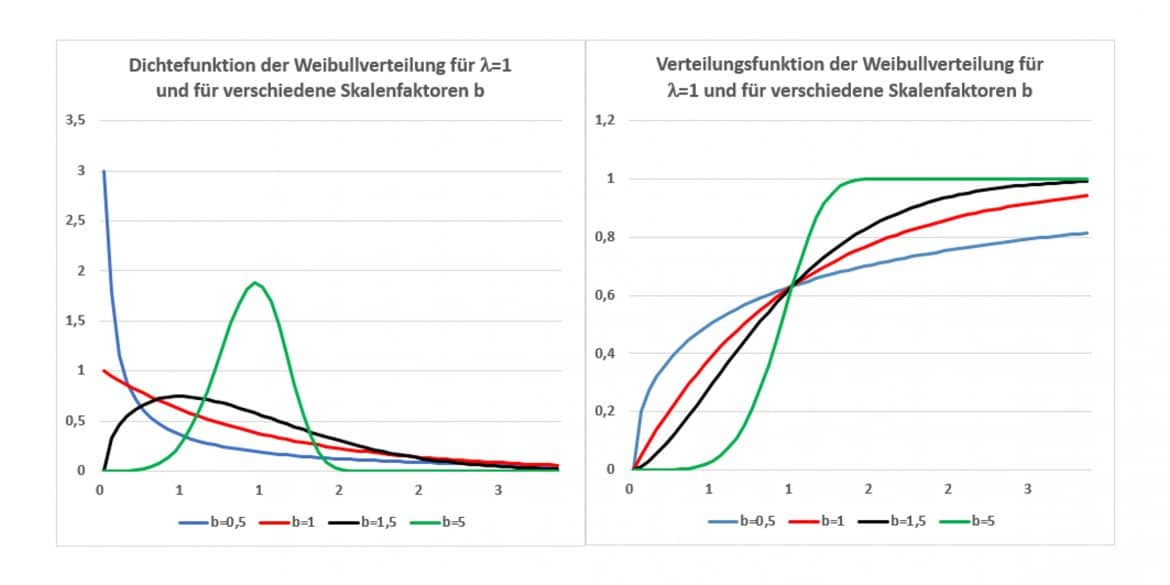
Die Grafiken zeigen den Verlauf von Dichte- und Verteilungsfunktion der Weibull-Verteilung für \lambda=1, es wird also eine mittlere Lebensdauer der Anlage von einer Periode angenommen. Änderungen von \lambda würden also eine horizontale Streckung oder Stauchung der Grafiken bewirken.

Nimmt der Formparameter einen Wert kleiner als eins an, wie etwa hier b=0,5 für die blauen Kurven, so nimmt die Dichte exponentiell ab und die Wahrscheinlichkeit, mit der maximal die Periode x erreicht wird, steigt außerdem unterproportional an.

Für b=1 erhältst Du dagegen die Exponentialverteilung, hier die roten Kurven.

Die grüne Kurve mit b=5 zeigt zunächst ansteigende, dann sinkende Werte der Dichtefunktion an, ähnlich denen der Normalverteilung.

Weibull-Verteilung

Für die Bestimmung von Erwartungswert und Varianz der Weibull-Verteilung benötigst Du zuerst die Gammafunktion:

    \begin{equation*} \Gamma(\alpha) = \int_0^{\infty}t^{\alpha-1} \cdot e^{-t} \nobreakspace dt, \quad f\"ur \nobreakspace \alpha >0 \quad \end{equation*}

mit den Eigenschaften

    \begin{equation*} \Gamma(\alpha+1)=\alpha \cdot \Gamma(\alpha) \quad und \quad \Gamma(1)=1 \end{equation*}

Du erhältst dann

    \begin{equation*} E(X)= \frac 1 {\lambda} \cdot \Gamma\left(1+\frac 1 b\right) \quad und \quad Var(X) =\frac 1 {\lambda^2} \left[\Gamma\left(1+\frac 2 b\right) - \Gamma^2\left(1+\frac 1 b\right)\right] \end{equation*}

Neben der Analyse von Ausfallwahrscheinlichkeiten von Anlagen findet die Weilbull-Verteilung zum Beispiel Anwendung in der Wettervorhersage für die Windkraftindustrie und in allgemeinen Versicherungsmodellen.