Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Normalverteilung / Gaußsche Glockenkurve
- 16. April 2018
- Posted by: Mika
Die Normalverteilung ist die in der Statistik wohl am häufigsten verwendete Verteilung. Das kommt zum einen daher, dass Du die Realisationen vieler naturwissenschaftlicher, technischer und wirtschaftlicher Variablen recht gut durch die Normalverteilung beschreiben kannst; zum anderen besagt der Zentrale Grenzwertsatz, dass der Mittelwert von n unabhängigen identisch verteilten Zufallsvariablen ![]() für große n gegen die Normalverteilung konvergieren, unabhängig von der Verteilung der
für große n gegen die Normalverteilung konvergieren, unabhängig von der Verteilung der ![]() .
.
Eigenschaften der Normalverteilung
Die Normalverteilung wird oft auch Gauß-Verteilung oder Gaußsche Glockenkurve genannt, da sie maßgeblich von dem Mathematiker Carl-Friedrich Gauß analysiert wurde und ihre Dichtefunktion eine Glockenform besitzt. Die Dichtefunktion ist symmetrisch und besitzt zudem die beiden Parameter Mittelwert ![]() und Varianz
und Varianz ![]() .
.
![]()
Integrierst Du die Dichtefunktion, so erhältst Du die zugehörige Verteilungsfunktion:
![]()
Visualisierung der Normalverteilung
Grafisch ergibt die Dichtefunktion der Normalverteilung wie links eine Glocke: Diese Form zeigt, dass Abweichungen vom Mittelwert nach oben oder nach unten umso unwahrscheinlicher werden, je weiter sie vom Mittelwert entfernt sind; die rechte Grafik zeigt die zugehörige Verteilungsfunktion:
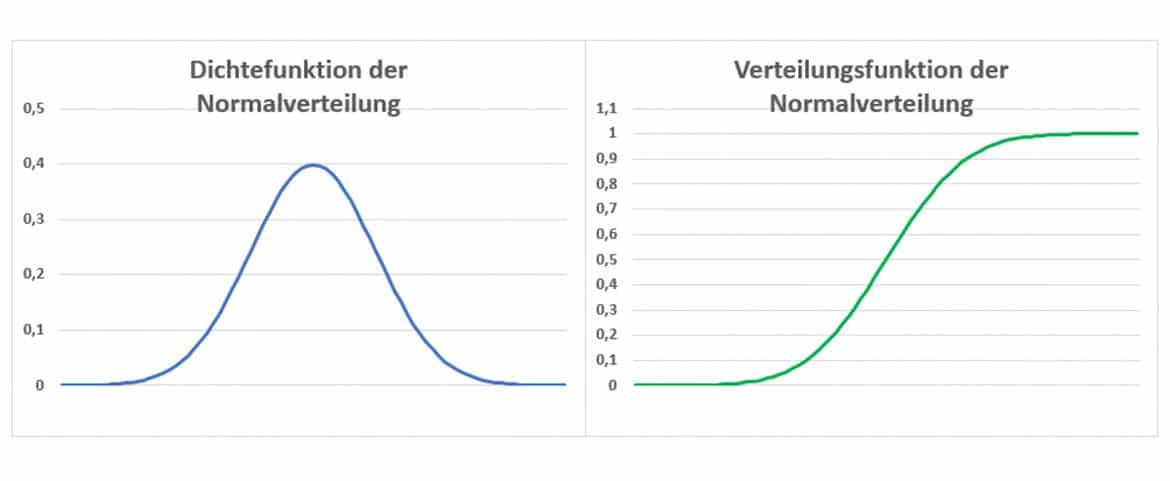
Je größer der Mittelwert der jeweiligen Verteilung ist, desto weiter rücken Dichte- und Verteilungsfunktion nach rechts; je größer die Varianz ist, umso breiter fallen beide aus.
Spezialfall: Standardnormalverteilung
Einen häufig verwendeten Spezialfall stellt die Standardnormalverteilung mit Mittelwert ![]() und Varianz
und Varianz ![]() dar, in die Du jede beliebige Normalverteilung überführen kannst, indem Du x in z standardisierst. Dazu subtrahierst Du den Mittelwert
dar, in die Du jede beliebige Normalverteilung überführen kannst, indem Du x in z standardisierst. Dazu subtrahierst Du den Mittelwert ![]() von Deinem x und dividierst die Differenz durch die Standardabweichung
von Deinem x und dividierst die Differenz durch die Standardabweichung ![]() , die Wurzel aus der Varianz.
, die Wurzel aus der Varianz.
![]()
Die Standardnormalverteilung liegt übrigens tabelliert vor und viele parametrische Schätz- und Testverfahren greifen auf sie zurück.
Anwendung der Normalverteilung
Eine Maschine soll beispielsweise Zucker in Paketen zu 1kg verpacken. Das Abfüllgewicht ist normalverteilt mit dem Mittelwert ![]() und hat außerdem eine Varianz von
und hat außerdem eine Varianz von ![]() . Du möchtest dann wissen, mit welcher Wahrscheinlichkeit höchstens ein Gewicht von 1,010 kg realisiert wird. Dazu standardisierst Du Deinen x-Wert in z und bestimmst den Wert der Verteilungsfunktion der Standardnormalverteilung an dieser Stelle:
. Du möchtest dann wissen, mit welcher Wahrscheinlichkeit höchstens ein Gewicht von 1,010 kg realisiert wird. Dazu standardisierst Du Deinen x-Wert in z und bestimmst den Wert der Verteilungsfunktion der Standardnormalverteilung an dieser Stelle:
![]()
Du erhältst folglich ![]() Deiner Zuckerpakete mit einem Gewicht von höchstens 1,01 kg.
Deiner Zuckerpakete mit einem Gewicht von höchstens 1,01 kg.
Im Gegensatz dazu kannst Du ermitteln, welches Gewicht mit einer Wahrscheinlichkeit von ![]() nicht überschritten wird. Dazu schaust Du in der Tabelle nach, welcher z-Wert zur Verteilungsfunktion an der Stelle
nicht überschritten wird. Dazu schaust Du in der Tabelle nach, welcher z-Wert zur Verteilungsfunktion an der Stelle ![]() gehört und findest den Wert z=1,645. Nach Umstellen obiger Formel der Standardisierung erhältst Du also:
gehört und findest den Wert z=1,645. Nach Umstellen obiger Formel der Standardisierung erhältst Du also:
![]()
Mit einer Wahrscheinlichkeit von ![]() liegt das Abfüllgewicht eines Paketes nicht über 1,0329 kg.
liegt das Abfüllgewicht eines Paketes nicht über 1,0329 kg.
Ausnutzen von Symmetrie
Wegen der Symmetrie der Normalverteilung gilt:
![]()
bzw.
![]()
Hiermit kannst Du aus Deinem obigen Ergebnis ganz leicht auch den Wert bestimmen, der nur mit einer Wahrscheinlichkeit von ![]() unterschritten wird. Du erhältst für -z=-1,645
unterschritten wird. Du erhältst für -z=-1,645
![]()
Mit einer Wahrscheinlichkeit von ![]() liegt das Abfüllgewicht unterhalb von 0,9671 kg.
liegt das Abfüllgewicht unterhalb von 0,9671 kg.
Interessant ist zudem auch, wieviel Prozent der Realisationen der Zufallsvariablen maximal einen Abstand in Höhe des Vielfachen der Standardabweichung vom Mittelwert aufweisen: Hier gilt für eine beliebige Normalverteilung:
![]()
![]()
und
![]()
Damit kannst Du erste Abschätzungen Deiner Verteilung sehr einfach vornehmen.
Für Dein Beispiel und das Zweifache der Standardabweichung ergeben sich als Intervallgrenzen, innerhalb derer ![]() der Realisationen liegen entsprechend
der Realisationen liegen entsprechend
![]()
Damit wiegen ![]() der Pakete also mindestens 960 g und höchstens 1040g. Der Hersteller sollte aber darüber nachdenken, die Maschine neu einzustellen, damit sich eine geringere Schwankungsbreite ergibt.
der Pakete also mindestens 960 g und höchstens 1040g. Der Hersteller sollte aber darüber nachdenken, die Maschine neu einzustellen, damit sich eine geringere Schwankungsbreite ergibt.
Im Falle, dass bestimmte Bedingungen vorliegen, insbesondere für große Stichprobenumfänge n, kannst Du andere Verteilungen durch die sehr einfach handhabbare Normalverteilung approximieren:
| Verteilung | Bedingung |
| Binomialverteilung | |
| Hypergeometrische Verteilung | |
| Poissonverteilung | |
| Student-Verteilung | |
| F-Verteilung |
