Lognormalverteilung

Lognormalverteilung

  • 16. April 2018
  • Posted by: Mika
Keine Kommentare

Du hast für Deine Zufallsvariable X formal dann eine Lognormalverteilung oder logarithmische Normalverteilung vorliegen, wenn die transformierte Zufallsvariable Z=ln(X) normalverteilt ist, mit den Parametern \mu_Z und \sigma^2_Z. Sie ist also eine stetige Verteilung.

Grafische Veranschaulichung

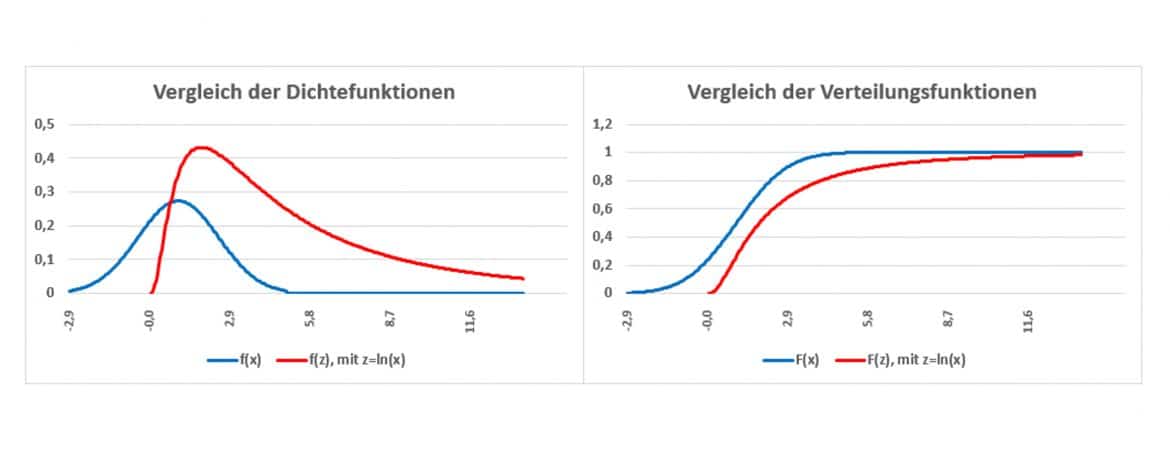
Die linke Grafik zeigt in blau die Dichtefunktion einer Normalverteilung mit den Parametern \mu=1,05 und \sigma^2= 1,4577, sowie rot die der logarithmierten Werte z, mit den Parametern \mu=0,6319 und \sigma^2= 0,9229. Du kannst deutlich erkennen, dass die Dichtefunktion der logarithmierten Werte erst im positiven Bereich der x-Achse beginnt und dass sie rechtsschief ist. Die rechte Grafik zeigt die zugehörigen Verteilungsfunktionen.

Lognormalverteilung

Praktisch findet die Lognormalverteilung Anwendung, wenn für x nur positive Werte in Frage kommen und im linken Bereich der Verteilung die Häufigkeiten größer sind als im rechten Bereich der Verteilung, wenn also eine rechtsschiefe Verteilung vorliegt. Ein klassischer Anwendungsfall ist beispielsweise die Verteilung von Gehältern, mit vielen kleinen Gehältern auf der linken Seite und einigen wenigen sehr hohen Gehältern auf der rechten Seite der Skala.

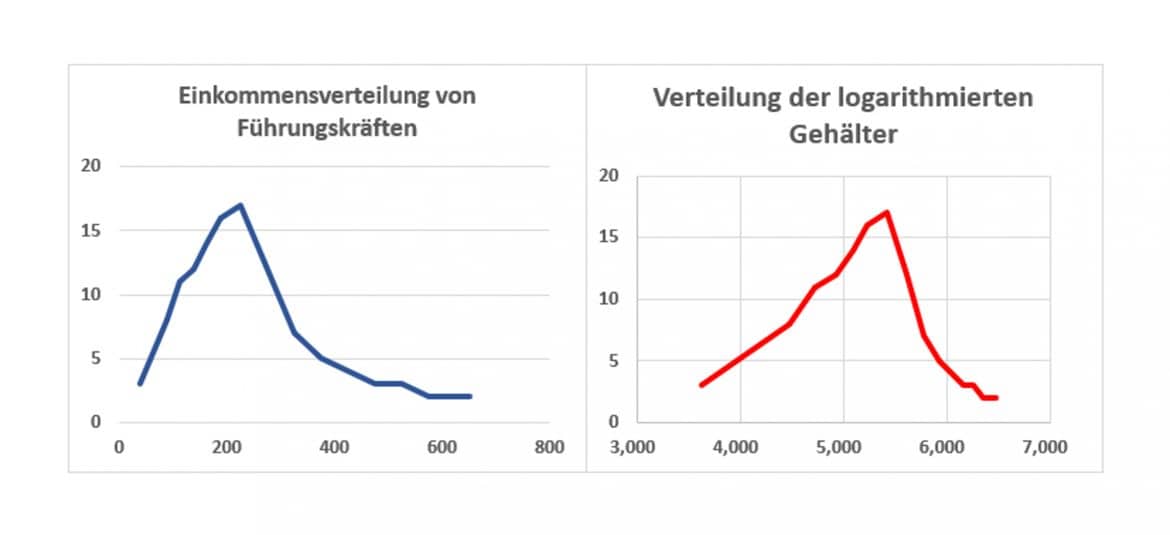
Die folgenden Häufigkeiten wurden für Führungskräfte einer spezifischen Branche erhoben:

Gehaltsklasse Klassenmitte
x		 log. Klassenmitte
z=ln(x)		 Häufigkeiten
bis 75 37,5 3,624 3
75-100 87,5 4,472 8
100-125 112,5 4,723 11
125-150 137,5 4,924 12
150-175 162,5 5,091 14
175-200 187,5 5,234 16
200-250 225,5 5,418 17
250-300 275,5 5,619 12
300-350 325,5 5,785 7
350-400 375,5 5,928 5
400-450 425,5 6,053 4
450-500 475,5 6,164 3
500-550 525,5 6,264 2
550-600 575,5 6,355 1
>600 650 6,477 2

Interpretation der Daten

Die linke Grafik zeigt die Häufigkeitsverteilung der Gehälter als blaues Liniendiagramm an, deutlich ist die schiefe Verteilung erkennbar. Die Annahme einer Normalverteilung wäre für diesen Datensatz also nicht brauchbar. Logarithmierst Du aber die Klassenmitten und betrachtest deren Verteilung, so wird diese deutlich symmetrischer und Du kannst eine Glockenform erahnen.

Lognormalverteilung

Für positive Werte von z erhältst Du die Dichtefunktion der Lognormalverteilung durch Einsetzen von z=ln(x) in die Dichtefunktion der Normalverteilung folglich zu

    \begin{equation*} f(z;\mu_Z,\sigma^2_Z) =f(ln(x);\mu_Z,\sigma^2_Z) =\frac 1 {\sigma_Z \sqrt{2\pi}}\cdot \frac 1 x \cdot e^{-\frac 1 2 (\frac {ln(x)-\mu_Z}{\sigma_Z})^2} \end{equation*}

Für negative Werte ist sie dagegen nicht definiert.
Die Parameter \mu_Z und \sigma^2_Z kannst Du als

    \begin{equation*} \mu_Z = e^ {\mu + \frac{\sigma^2} 2} \quad und \quad \sigma^2_Z = e^{2 \cdot \mu + \sigma^2}\cdot (e{^{\sigma^2}}-1). \end{equation*}

berechnen.