Gamma-Verteilung

Gamma-Verteilung

  • 16. April 2018
  • Posted by: Mika
Keine Kommentare

Definiert für nicht negative reelle Zahlen ist die Gammaverteilung wie die Weibull-Verteilung eine stetige Verteilung mit zudem zwei (positiven) Parametern, erstens dem Skalenparameter \theta und zweitens dem Formparameter k. Dabei ist \theta die mittlere Eintrittswahrscheinlichkeit für das betrachtete Ereignis pro Intervall und durch k berücksichtigst Du außerdem deren Veränderung im Zeitablauf.

Damit ist die Gamma-Verteilung an empirische Gegebenheiten flexibel anpassbar und wird in verschiedensten Bereichen eingesetzt, beispielsweise beim Design von Versicherungskonditionen, zur Modellierung der genetischen Prägung und für die Kalkulation der benötigten Größe von Wasserreservoirs basierend auf der Menge der Regenfälle.

Charakterisierung der Gamma-Verteilung

Dichte-und Verteilungsfunktion der Gamma-Verteilung sind mit der Gamma-Funktion formuliert, das heißt konkret:

    \begin{equation*} \Gamma(\alpha) = \int_0^{\infty}t^{\alpha-1} \cdot e^{-t} \nobreakspace dt, \quad f\"ur \nobreakspace \alpha >0 \quad \end{equation*}

Dabei gilt:

    \begin{equation*} \Gamma(\alpha+1)=\alpha \cdot \Gamma(\alpha) \quad und \quad \Gamma(1)=1 \end{equation*}

Eine gamma-verteilte Zufallsvariable X besitzt einerseits die Dichtefunktion

    \begin{equation*} f(x;\theta,k)=\frac {x^{k-1}\cdot e^{-\frac x {\theta}}}{\theta^k\cdot \Gamma(k)}\quad f\"ur \nobreakspace x >0 \quad und \quad \theta,k>0 \end{equation*}

und andererseits die Verteilungsfunktion

    \begin{equation*} F(x;\theta,k)=\int_0^x \nobreakspace \frac {u^{k-1}\cdot e^{-\frac u {\theta}}}{\theta^k\cdot \Gamma(k)} \nobreakspace du \end{equation*}

Der Skalierungsparameter \theta für die mittlere Eintrittswahrscheinlichkeit streckt oder staucht beide Funktionen in der Horizontalen. Unterschiedliche k-Werte modellieren dagegen unterschiedliche Veränderungen der Eintrittswahrscheinlichkeit im Zeitlablauf.

Die Grafiken zeigen Dichte- und Verteilungsfunktionen von Gamma-Verteilungen mit \theta=0,5 und unterschiedlichen Werten des Formparameters k:

Gamma-Verteilung

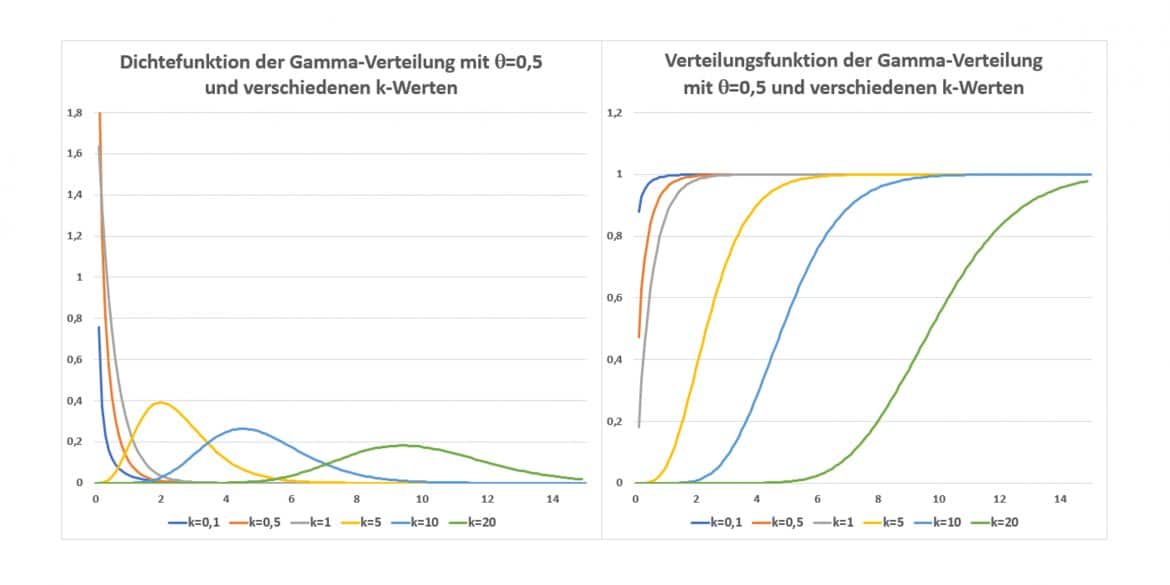
Für k=1 erhältst Du mit den grauen Kurven den Spezialfall der Exponentialverteilung.
Erwartungswert und Varianz berechnest Du außerdem zu

    \begin{equation*} E(X)=k\cdot\theta \quad und \quad Var(X)=k \cdot \theta^2 \end{equation*}