Dichtefunktion

Dichtefunktion

  • 16. April 2018
  • Posted by: Mika
Keine Kommentare

Während Du bei einer diskreten Zufallsvariable nur endlich viele mögliche Beobachtungswerte gegeben hast, zu denen jeweils eine positive Wahrscheinlichkeit gehört, gibt es im stetigen Fall unendlich viele theoretisch mögliche Realisationen.

Die Wahrscheinlichkeit, mit der ein bestimmter Wert eintritt, als Anzahl der günstigen durch Anzahl der (im stetigen Fall \infty vielen) möglichen Werte, ist dementsprechend für alle Werte gleich null. Daher gibt es bei stetigen Zufallsvariablen keine Wahrscheinlichkeitsfunktion.

An ihre Stelle tritt in diesem Fall die Dichtefunktion als ein Maß dafür, wie dicht die Realisationen der Zufallsvariablen X um den Wert x liegen. Je mehr Realisationen sich an einer Stelle scharen, umso höher ist die Dichte dort und umso größer ist die Wahrscheinlichkeit, dass eine Realisation „in der Nähe“ von x beobachtet wird.

Eigenschafaten der Dichtefunktion

  • Sie ist nie kleiner als null, kann aber, anders als die Wahrscheinlichkeitsfunktion, auch Werte größer als eins annehmen:

        \begin{equation*} f(x) \ge 0 \quad f\"ur \nobreakspace alle \nobreakspace x \in \mathbb{R} \end{equation*}

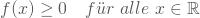
  • Das Integral über die Dichtefunktion von 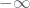-\infty bis \infty ergibt außerdem eins:

        \begin{equation*} \int_{-\infty}^{\infty} f(x) \nobreakspace dx = 1 \end{equation*}

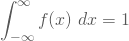
  • Durch Integrieren der Dichtefunktion bis zum Wert x erhältst Du zudem die zugehörige Verteilungsfunktion F(x):

        \begin{equation*} F(x) = \int_{-\infty}^{x} f(x) \nobreakspace dx, \quad f\"ur \nobreakspace x \in \mathbb{R} \end{equation*}

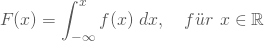
Folglich kannst Du die Wahrscheinlichkeit für das Auftreten einer Realisation der Zufallsvariablen im Intervall [a;b] als Differenz der Werte der Verteilungsfunktion an den Stellen b und a berechnen:

    \begin{equation*} Prob(a < x\le b) = F(b)-F(a) = \int_a^b f(x) \nobreakspace dx, f\"ur \nobreakspace a\le b \end{equation*}

Dichtefunktion

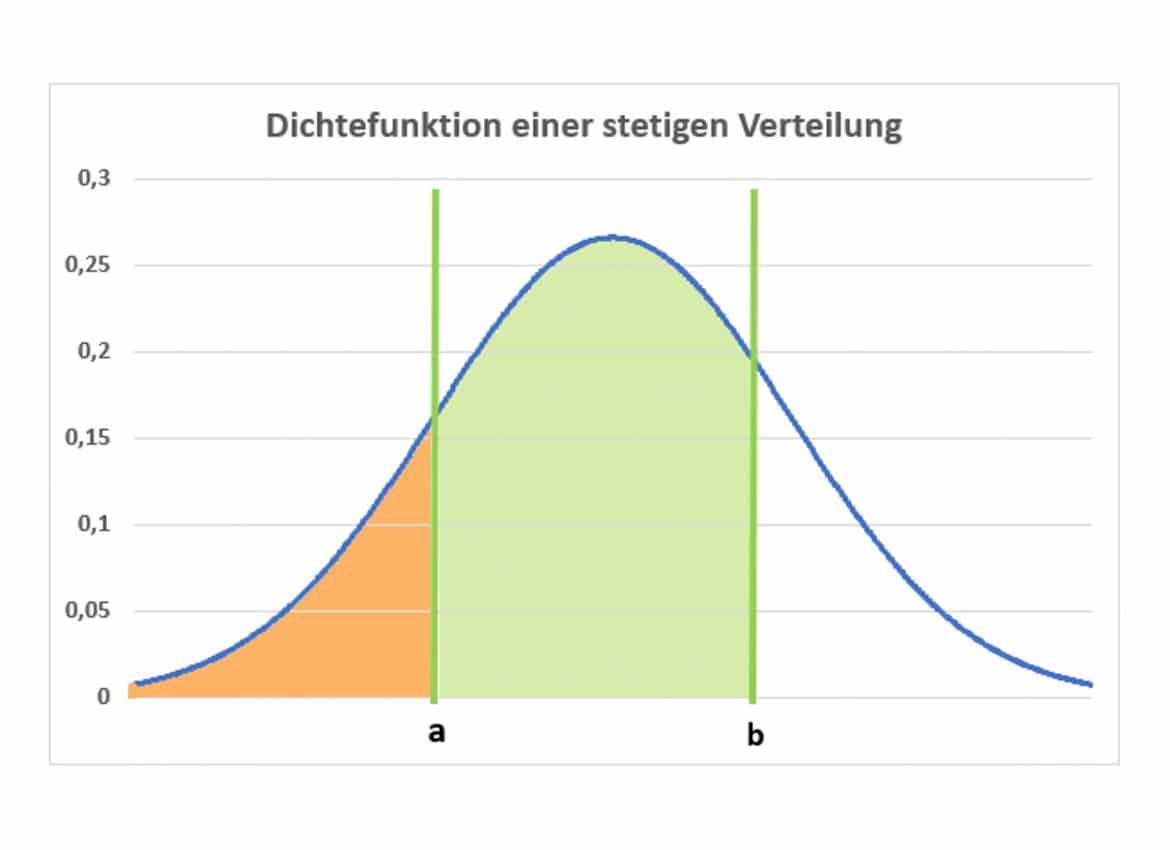
Die Grafik zeigt blau eingezeichnet eine Dichtefunktion; die orangene Fläche ist das Integral über die Dichtefunktion von -\infty bis a und ergibt den Wert der Verteilungsfunktion an der Stelle a. Das ist die Wahrscheinlichkeit, mit der höchstens ein Wert von a auftritt; die gelbe und grüne Fläche gemeinsam stellen den Wert der Verteilungsfunktion an der Stelle b dar. Ihre Differenz, die grüne Fläche, gibt Dir die Wahrscheinlichkeit an, mit der Du eine Realisation der Zufallsvariablen zwischen a und b beobachten kannst.