Beta-Verteilung

Beta-Verteilung

  • 16. April 2018
  • Posted by: Mika
Keine Kommentare

Die Beta-Verteilung ist eine stetige Verteilung mit den beiden positiven Parametern p und q, die außerdem innerhalb des Intervalls [0;1] definiert ist. Indem Du unterschiedliche Werte für die Parameter p und q einsetzt, können Dichte- und Verteilungsfunktion sehr unterschiedliche Gestalten annehmen, wodurch die Verteilung sehr flexibel einsetzbar ist.

Charakterisierung der Beta-Verteilung

Die Dichtefunktion der Beta-Verteilung lautet:

    \begin{equation*} f(x;p,q)=\begin {cases} 0, \quad f\"ur \nobreakspace x < 0 \\ \\ \frac 1 {B(p,q)} \cdot x^{p-1} \cdot (1-x)^{q-1}, \quad f\"ur 0 \le x \le 1, \quad mit \nobreakspace p,q>0 \\ \\ 0, \quad f\"ur \nobreakspace x >1 \end{equation*}

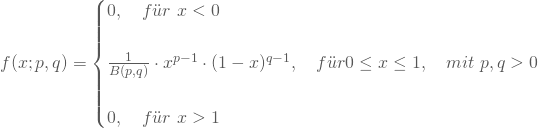
Dabei ist der erste Faktor der Dichtefunktion ein Normierungsfaktor, der folglich dafür sorgt, dass das Integral über der Dichtefunktion im Intervall [0,1] den Wert Eins annimmt. In dessen Nenner ist zudem die Betafunktion enthalten, die definiert ist als

    \begin{equation*} B(p,q) = \int_0^1 u^{p-1} \cdot (1-u)^{q-1}\nobreakspace du \end{equation*}

B(p,q) berechnet also die Fläche unter der nicht normierten Dichtefunktion im Intervall [0;1].
Außerhalb von [0;1] beträgt der Wert der Dichtefunktion immer Null.
Die Verteilungsfunktion erhältst Du dann zu

    \begin{equation*} F(x;p,q)=\begin {cases} 0, \quad f\"ur \nobreakspace x < 0 \\ \\ \frac {B(x;p,q)} {B(p,q)}, \quad f\"ur 0 \le x \le 1, \quad mit \nobreakspace p,q>0 \\ \\ 1, \quad f\"ur \nobreakspace x >1 \end{equation*}

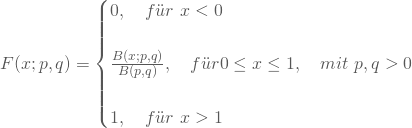
Die unvollständige Betafunktion

B(x;p,q) ist übrigens die unvollständige Betafunktion, die das Integral unter der nicht normierten Dichtefunktion im Intervall [0;x] angibt.

    \begin{equation*} B(x;p,q) = \int_0^x u^{p-1} \cdot (1-u)^{q-1}\nobreakspace du \end{equation*}

Beta-Verteilung

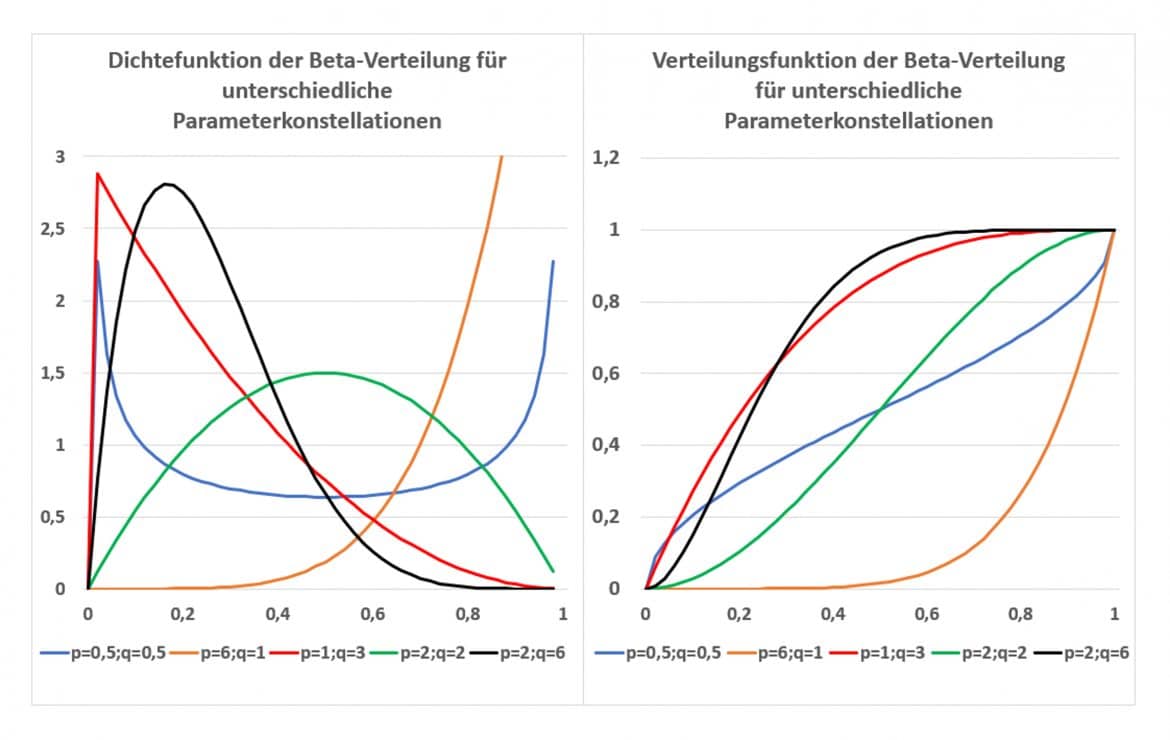
Die Grafiken zeigen die sehr unterschiedlichen Formen von Dichte- und Verteilungsfunktion je nach Wahl der Parameter. Dementsprechend kannst Du die Verteilung beim empirischen Arbeiten sehr individuell an Dein Datenmaterial anpassen. Für p=q=1 ergibt sich zudem die stetige Gleichverteilung.
Weiterhin erhältst Du Erwartungswert und Varianz der Beta-Verteilung als

    \begin{equation*} E(X)=\left(\begin {array} {11} p\\p+q\end{array}\right) \quad und \quad Var(X)=\left(\begin {array} {11} pq\\(p+q+1)\cdot(p+q)^2\end{array}\right) \end{equation*}