Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Stetige Verteilungen
- 16. April 2018
- Posted by: Mika
Du sprichst von einer stetigen Verteilung, wenn die zugehörige Zufallsvariable alle reellen Werte innerhalb eines Intervalls annehmen kann; die Zufallsvariable ist dann stetig. Da jedes Intervall in unendlich viele Teile unterteilt werden kann, beträgt dann die Wahrscheinlichkeit dafür, dass ein bestimmter Wert auftritt, für alle Werte Null. Bei diskreten Verteilungen dagegen gibt es nur abzählbar viele Realisationen von X, zu denen positive Wahrscheinlichkeiten gehören.
Beschreibung mittels Dichtefunktion
An die Stelle der Wahrscheinlichkeitsfunktion tritt daher bei stetigen Verteilungen die Dichtefunktion f(x), die ein Maß dafür ist, wie dicht sich mögliche Werte von X um den Wert x scharen; ihr Integral über ein beliebiges Intervall gibt die Wahrscheinlichkeit an, mit der eine Realisation von X in diesem Integral liegt.
Die Verteilungsfunktion F(x) gibt die Wahrscheinlichkeit an, mit der ein beobachteter Wert kleiner oder gleich x ist; formal erhältst Du sie als Integral über die Dichtefunktion von ![]() bis x.
bis x.
Ein Beispiel für eine stetige Zufallsvariable ist die Füllmenge von Joghurtbechern: eine Maschine, die die Becher befüllt, hat eine Vorgabemenge von 150 g Gramm eingestellt, die aber ganz exakt nicht realisiert werden kann. Stattdessen kannst Du à priori nicht bestimmbare Abweichungen nach oben oder unten innerhalb eines Intervalls beobachten.
Eine Stichprobe vom Umfang 20 ergibt beispielsweise die folgenden Messwerte und Abweichungen von der Sollfüllmenge:
| lfd.Nr. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Gewicht | 150,32 g | 149,87 g | 149,61 g | 149,88 g | 150,59 g | 150,85 g | 149,06 g | 149,22 g | 150,18 g | 150,85 g | 150,67 g | 150,44 g | 150,62 g | 149,66 g | 149,66 g | 150,67 g | 150,40 g | 150,14 g | 150,71 g | 150,22 g |
| Abweichung | -0,32 g | 0,13 g | 0,39 g | 0,12 g | -0,59 g | -0,85 g | 0,94 g | 0,78 g | -0,18 g | -0,85 g | -0,67 g | -0,44 g | -0,62 g | 0,34 g | 0,34 g | -0,67 g | -0,40 g | -0,14 g | -0,71 g | -0,22 g |
Grafisch dargestellt hast Du also folgende Abweichungen beobachtet:
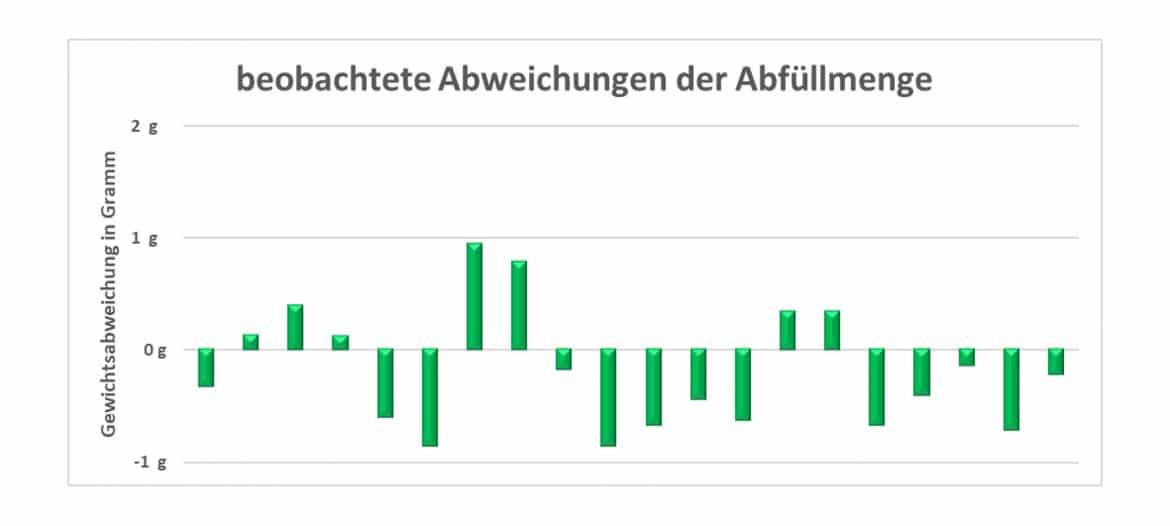
Um anhand Deiner Beobachtungen möglichst präzise statistische Aussagen über die Abweichungen der Grundgesamtheit treffen zu können, musst Du aus den stetigen Verteilungen die geeignete auswählen.
Übersicht über die stetigen Verteilungen
| Verteilung | Eigenschaften |
| Gleichverteilung | Alle möglichen Realisationen der Zufallsvariablen besitzen die gleiche Dichte und die Verteilungsfunktion verläuft linear. Die Gleichverteilung verwendet man in der Marktforschung oft, wenn noch keine Informationen über die Präferenzen der Zielgruppe bekannt sind. |
| Normalverteilung | Die Normalverteilung stellt die am häufigsten verwendete Verteilung dar; ein symmetrischer glockenförmiger Verlauf der Dichtefunktion passt auf viele empirische Phänomene. Die Normalverteilung hat zwei Parameter |
| Lognormalverteilung | Die Lognormalverteilung ist die Normalverteilung der logarithmierten Werte der Zufallsvariablen und ist bei rechtsschiefen Verteilungen anzuwenden. |
| Laplace-Verteilung | Die Laplace-Verteilung ist eine symmetrische Verteilung mit spitzem Bereich in der Mitte der Dichtefunktion, sie wird wegen Ihres Aussehens auch doppelte Exponentialverteilung genannt. |
| Exponentialverteilung | Der exponentielle Verlauf der Dichtefunktion ist hier namensgebend. Die Exponentialverteilung verwendet man oft, um Aussagen über die Länge zufälliger Zeitintervalle zu treffen. |
| Weibull-Verteilung | Die Weibull-Verteilung ist mit Skalen- und Formparameter sehr flexibel einsetzbar, oft wird sie wie die Exponentialverteilung für Aussagen über die Länge zufälliger Zeitintervalle verwendet, wobei die Weibull-Verteilung Änderungen im Zeitablauf zu berücksichtigen vermag. |
| Gamma-Verteilung | Skalen- und Formparameter ermöglichen die Modellierung vieler verschiedener Dichte- und Verteilungsfunktionen und sehr vielseitige Einsatzmöglichkeiten der Gammaverteilung. |
| Betaverteilung | Die Beta-Verteilung ist eine Verteilung mit zwei Parametern, deren Auswahl sehr unterschiedliche Gestaltung von Dichte- und Verteilungsfunktion ermöglicht. |
