Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Poisson-Verteilung
- 16. April 2018
- Posted by: Mika
Du verwendest die Poisson-Verteilung, wenn Du ein Bernouilli-Experiment n mal unabhängig voneinander durchführst und eine sehr kleine Erfolgswahrscheinlichkeit p vorliegt. Sie liefert Dir dann die Wahrscheinlichkeit, mit der das Ereignis bei n Wiederholungen in einem Zeitintervall genau k mal beobachtet wird. Wegen der kleinen Erfolgswahrscheinlichkeit wird die Poisson-Verteilung auch Verteilung der seltenen Ereignisse genannt.
Beispiel für eine Poisson-Verteilung
Eine regionale Kfz-Versicherung benötigt zum Beispiel für die Erstellung ihrer Tarife die Wahrscheinlichkeiten, mit denen in einem Jahr 1, 2 oder 3 Autos einen Unfall haben. Aus den vorherigen Jahren kennst Du die Unfallwahrscheinlichkeit für ein Auto als p = 0,000445. Dann kannst Du bei bekanntem n, etwa n=10000 Autos, die erwartete Anzahl von Unfällen als
![]()
berechnen. Diese erwartete Anzahl von Unfällen bezeichnest Du weiterhin als ![]() . Sie geht dann in die Wahrscheinlichkeits- und Verteilungsfunktion ein, welche lautet:
. Sie geht dann in die Wahrscheinlichkeits- und Verteilungsfunktion ein, welche lautet:
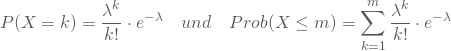
Damit kannst Du für Dein Beispiel die Wahrscheinlichkeit errechnen, mit der genau k Unfälle auftreten; Kumulierend erhältst Du dementsprechend Deine Verteilungsfunktion:
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Wahr- scheinlich- keits- funktion |
0,012 | 0,052 | 0,116 | 0,172 | 0,191 | 0,170 | 0,126 | 0,080 | 0,045 | 0,022 | 0,010 | 0,004 | 0,001 |
| Ver- teilungs- funktion |
0,012 | 0,064 | 0,179 | 0,351 | 0,542 | 0,711 | 0,837 | 0,917 | 0,962 | 0,984 | 0,994 | 0,998 | 0,999 |
Grafische Darstellung
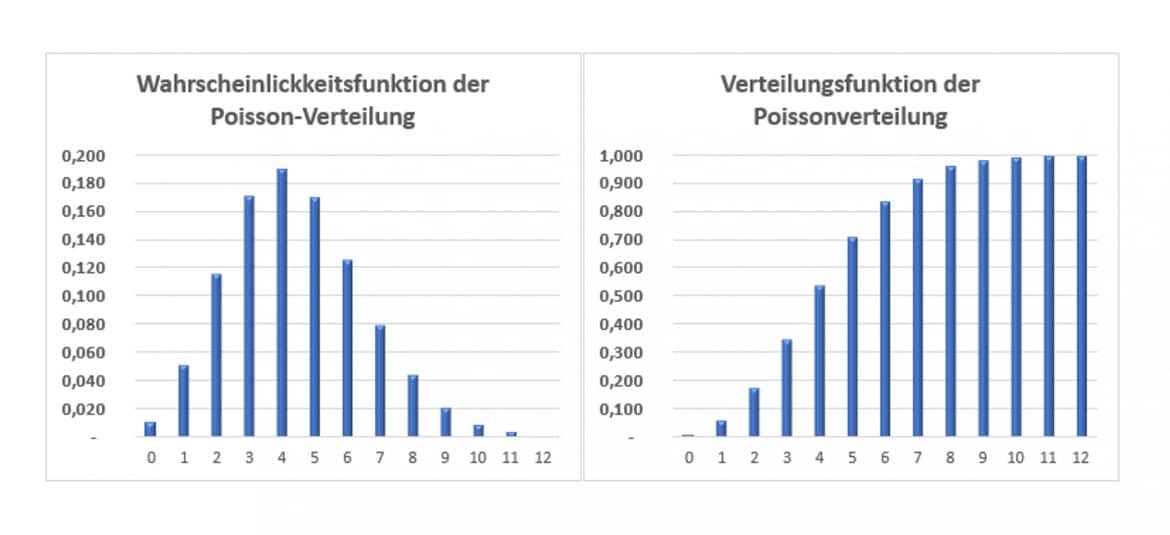
Die Poisson-Verteilung, die nur von ![]() abhängt, liegt übrigens tabelliert vor. Sie benötigt zudem die gleichen Voraussetzungen wie die Binomialverteilung und wird bei sehr kleinem p eingesetzt. Damit brauchst Du sie für
abhängt, liegt übrigens tabelliert vor. Sie benötigt zudem die gleichen Voraussetzungen wie die Binomialverteilung und wird bei sehr kleinem p eingesetzt. Damit brauchst Du sie für
- punktuelle Ereignisse im Zeitverlauf, wie beispielsweise Geburten, vorbeifahrende Autos, Telefonanrufe, etc.,
- die unabhängig voneinander sind (Bernouilli-Experiment), und
- deren Intensität im Zeitverlauf konstant ist.
