Multinomialverteilung

Multinomialverteilung

  • 16. April 2018
  • Posted by: Mika
Keine Kommentare

Die Multinomialverteilung ist eine Verallgemeinerung der Binomialverteilung. Zudem gehört sie zu den diskreten Wahrscheinlichkeitsverteilungen. Bei beiden wird ein Zufallsexperiment n mal unabhängig wiederholt und Du suchst dann die Wahrscheinlichkeiten, mit denen sich bestimmte Experimentausgänge ergeben. Während bei der Binomialverteilung allerdings nur zwei mögliche Experimentausgänge betrachtet werden, lässt die Multinomialverteilung k \le n verschiedene Ausgänge zu.

In einer Spielhalle wird beispielsweise ein Spiel ähnlich dem Roulette gespielt: Ein Rad ist in 5 Sektoren aufgeteilt, von denen zwei Sektoren rot (R), zwei Sektoren schwarz (S) sind und ein Sektor weiß (W) ist. Es gibt also k=3 mögliche Ausgänge des Zufallsexperimentes. Ein Spieler kann entweder auf rot oder auf schwarz setzen. Es wird eine Kugel geworfen: Landet sie auf der Farbe, auf die der Spieler gesetzt hat, so gewinnt er; landet sie auf weiß, so gewinnt dementsprechend die Bank.

Für jedes einzelne Spiel sind die Wahrscheinlichkeiten, mit der die Kugel auf einer bestimmten Farbe landet, durch die Anzahl der Sektoren gegeben:

    \begin{equation*} p_R = \frac 2 {5} = 0,4, \quad p_S = \frac 2 5=0,4 \quad und \quad p_W = \frac 1 5 = 0,2 \end{equation*}

Du suchst nun die Wahrscheinlichkeiten dafür, dass bei n=6 Würfen der Kugel etwa n_1=n_R=3 mal rot, n_2=n_S=2 mal schwarz geworfen wird und dass die Kugel n_3=n_W=1 mal auf dem weißen Sektor landet, mit n_1+n_2+n_3=n.

Wie berechnet man diese Wahrscheinlichkeit?

Du beginnst damit, die Wahrscheinlichkeit für das Eintreten einer Abfolge von Farben, für die diese Anforderung erfüllt ist, zu berechnen:

    \begin{equation*} P(RRRSSW) = 0,4^3 \cdot 0,4^2 \cdot 0,2^1= \end{equation*}

Anschließend ermittelst Du die Anzahl von Kombinationen an Farbfolgen, die die gegebene Anforderung erfüllen, als Multinomialkoeffizient:

    \begin{equation*} \left(\begin {array} {11} n \\{n_1,n_2,n_3}\end{array}\right) = \frac {n!}{n_1! \cdot n_2! \cdot n_3!},\quad mit \quad n_1+n_2+n_3 = n \end{equation*}

Für Dein Beispiel gibt es demnach

    \begin{equation*} \left(\begin {array} {11} n \\{3,2,1}\end{array}\right) = \frac {6!}{3! \cdot 2! \cdot 1!} = 60 \end{equation*}

verschiedene Abfolgen von Sektoren, auf denen die Kugel landet, die die Anforderung 3 mal rot, 2 mal schwarz und einmal weiß erfüllen.

Wegen des Kommutativgesetzes, gemäß dem die Reihenfolge der Faktoren bei der Multiplikation beliebig getauscht werden kann, tritt jede dieser Kombinationen mit der gleichen Wahrscheinlichkeit von 0,0020 ein.

Daher erhältst Du als Wahrscheinlichkeit, bei 6 Würfen dreimal auf rot, zweimal auf schwarz und einmal auf weiß zu landen, den Wert 0,12:

    \begin{equation*} P(3,2,1|6;0,4;0,4;0,2) =\left(\begin {array} {11} 6 \\{3,2,1}\end{array}\right) \cdot 0,4^3 \cdot 0,4^2 \cdot 0,2^1 = 60 \cdot 0,0020 = 0,12 \end{equation*}

Wahrscheinlichkeitsfunktion der Multinomialverteilung

Die allgemeine Wahrscheinlichkeitsfunktion der Multinomialverteilung lautet:

    \begin{equation*} P(n_1,..,n_k|n;p_1,..,p_k) =\left(\begin {array} {11} n \\{n_1\cdot ..\cdot n_k}\end{array}\right) \cdot p_1^{n1} \cdot ... \cdot p_k^{n_k}, \quad mit \nobreakspace\sum_{i=1}^k n_i =n \nobreakspace und \sum_{i=1}^k p_i=1 \end{equation*}

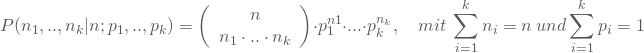
Die Verteilungsfunktion erhältst Du wieder durch Kumulieren der Wahrscheinlichkeitsfunktion, wobei Du jeweils die Bedingung \sum_{i=1}^k n_i =n einhalten musst.

Als Momente der Multinomialverteilung kannst Du Erwartungswert und Varianz für die möglichen Experimentausgänge einzeln berechnen. Dabei kannst Du ausnutzen, dass es für jeden Ausgang immer nur die Möglichkeit gibt, dass er eintritt oder nicht eintritt, er also binomialverteilt ist. Damit lauten die Erwartungswerte:

    \begin{equation*} \mu_i = n \cdot p_i, \quad f\"ur \nobreakspace i=1,..,k \end{equation*}

Für Dein Beispiel also:

    \begin{equation*} \mu_R=6\cdot 0,4=2,4; \nobreakspace\mu_S=6\cdot 0,4=2,4 \nobreakspace und \nobreakspace\mu_W=6\cdot 0,2=1,2 \end{equation*}

Bei sechsmaligem Werfen der Kugel sollte also im Mittel 2,4-mal rot, 2,4-mal schwarz und 1,2-mal weiß fallen.

Die zugehörigen Varianzen erhältst Du als

    \begin{equation*} \sigma^2_i = n \cdot p_i \cdot (1-p_i), \quad f\"ur \nobreakspace i=1,..,k \end{equation*}

zu

    \begin{equation*} \sigma^2_R = \sigma^2_S = 6 \cdot 0,4 \cdot 0,6 = 1,44 \quad und \quad \sigma^2_W = 6 \cdot 0,2 \cdot 0,8 = 0,96 \end{equation*}