Hypergeometrische Verteilung

Hypergeometrische Verteilung

  • 16. April 2018
  • Posted by: Mika
Keine Kommentare

Führst Du ein Zufallsexperiment mit zwei mögliche Ausgänge x_1 und x_2, die mit den Wahrscheinlichkeiten p und (1-p) auftreten, n mal durch, wobei die Durchgänge abhängig voneinander sind, so gilt hier die hypergeometrische Verteilung für die Häufigkeit des Auftretens des Ausgangs x_1. Bezogen auf das Urnenmodell mit Kugeln in zwei Farben spricht man dann vom Ziehen ohne Zurücklegen: Nimmst Du eine Kugel aus der Urne heraus und legst sie nicht wieder zurück, so ändern sich dementsprechend die Laplace-Wahrscheinlichkeiten als die Anzahl der günstigen durch die Anzahl der möglichen Fälle.

Die n=8 Teilnehmer einer Verkaufsveranstaltung dürfen beispielsweise an einer Verlosung teilnehmen. Dazu steht eine Box mit N=50 Losen, von denen M=2 je eine Urlaubsreise gewinnen lässt und (N-M)=48 Nieten darstellen. Die Teilnehmer möchten ferner wissen, mit welcher statistischen Wahrscheinlichkeit bei ihrer Ziehung 0, 1 oder 2 Gewinne gezogen werden.
Die Anzahl der Möglichkeiten, aus einer Grundgesamtheit vom Umfang N eine Stichprobe vom Umfang n zu ziehen, kennst Du aus der Kombinatorik entsprechend als \left(\begin {array} {11} N \\n\end{array}\right).

Anzahl an Möglichkeiten

Die Anzahl der unterschiedlichen Möglichkeiten, 8 Lose aus einer Box von 50 Losen zu ziehen, beträgt also

    \begin{equation*} $\left(\begin {array} {11} N \\n\end{array}\right)=\left(\begin {array} {11} 50 \\8\end{array}\right) =\frac {50!}{8! \cdot 42!} \end{equation*}

Für die günstigen Fälle multiplizierst Du außerdem die Anzahl der Möglichkeiten, k aus M Gewinnlosen anzuordnen mit der Anzahl der Möglichkeiten, (n-k) aus (N-M)=48 zu ziehen. Für k=0 heißt das:

    \begin{equation*} \left(\begin {array} {11} 2 \\k\end{array}\right) \cdot \left(\begin {array} {11} 48 \\(8-k)\end{array}\right) = \frac {2!}{0! \cdot 2!} \cdot \frac {48!}{8! \cdot 40!}, \quad f\"ur \nobreakspace k=0 \end{equation*}

Wie sieht die Wahrscheinlichkeitsfunktion aus?

Teilst Du anschließend für die Wahrscheinlichkeit die Anzahl der günstigen durch die der möglichen Fälle, so erhältst Du die Wahrscheinlichkeitsfunktion der Hypergeometrischen Verteilung:

    \begin{equation*} P(X=0) = \frac {\left(\begin {array} {11} 2 \\0\end{array}\right) \cdot \left(\begin {array} {11} 48 \\8\end{array}\right)} {\left(\begin {array} {11} 50 \\8\end{array}\right) } = \frac {2! \cdot 48! \cdot 8! \cdot 42!}{ 2! \cdot 8! \cdot 40! \cdot 50!} = 0,7029 \end{equation*}

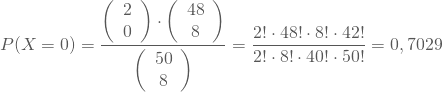
Entsprechend kannst du die Wahrscheinlichkeiten für k=1 und k=2 berechnen:

    \begin{equation*} P(X=1) = \frac {\left(\begin {array} {11} 2 \\1\end{array}\right) \cdot \left(\begin {array} {11} 48 \\7\end{array}\right)} {\left(\begin {array} {11} 50 \\8\end{array}\right) } = 0,2743 \quad und \quad P(X=2) = \frac {\left(\begin {array} {11} 2 \\2\end{array}\right) \cdot \left(\begin {array} {11} 48 \\6\end{array}\right)} {\left(\begin {array} {11} 50 \\8\end{array}\right) } = 0,0229 \end{equation*}

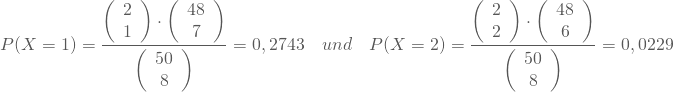
Als Momente der Hypergeometrischen Verteilung hast Du einerseits den Erwartungswert

    \begin{equation*} \mu = n \cdot p, \quad mit \nobreakspace p=\frac M N \end{equation*}

und andererseits die Varianz

    \begin{equation*} \sigma^2 = \frac {N-n}{N-1} \cdot n \cdot p \cdot (1-p), \quad mit \nobreakspace p= \frac M N \end{equation*}

Für Dein Beispiel ergibt sich also:

    \begin{equation*} \mu = n \cdot p =8\cdot \frac 2 {50} = 0,32 \end{equation*}

und

    \begin{equation*} \sigma^2 = \frac {N-n}{N-1} \cdot n \cdot p \cdot (1-p) = \frac {42} {49} \cdot 8 \cdot \frac 2 {50} \cdot \frac {48} {50} = 0,2633 \end{equation*}

Die hypergeometrische Verteilung nähert sich für große N und kleine p übrigens an die Binomialverteilung an; Du kannst sie durch die tabelliert vorliegende Binomialverteilung approximieren, falls N \ge 2000 und p<0,1.