Gleichverteilung

Gleichverteilung

  • 16. April 2018
  • Posted by: Mika
Keine Kommentare

Kann Dein Zufallsexperiment nur zu einer endlichen Anzahl von Ausgängen führen, die alle mit der gleichen Wahrscheinlichkeit eintreten, so liegt bei der dazugehörigen Zufallsvariablen eine Gleichverteilung vor. Dabei kann es sein, dass die Wahrscheinlichkeiten wie bei einem (theoretisch) symmetrischen Würfel tatsächlich alle gleich sind oder dass sie mangels weiterer Informationen als gleich angenommen werden.

Für die Wahrscheinlichkeiten p_i der n möglichen Realisationen x_1 bis x_n Deiner Zufallsvariablen X gilt also:

    \begin{equation*} p_i = P(X=x_i) = P(X=x_j) = p_j \quad f\"ur \nobreakspace beliebige \nobreakspace i \nobreakspace und \nobreakspace j,\nobreakspace mit \nobreakspace i,j=1\nobreakspace bis \nobreakspace n \end{equation*}

.

Außerdem ist die Summe der p_i als die Wahrscheinlichkeit, dass irgendeiner der möglichen Ausgänge des Zufallsexperimentes, das sichere Ereignis eintritt, gleich Eins.

    \begin{equation*} \sum_{i=1}^n p_i = P(\bigcup_{i=1}^n x_i) = 1 \end{equation*}

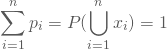
Setzt Du die erste Gleichung dann in die zweite ein, so erhältst Du die Einzelwahrscheinlichkeiten:

    \begin{equation*} \sum_{i=1}^n p_i = n \cdot p_i = 1, \nobreakspace also \nobreakspace p_i = \frac 1 n \nobreakspace f\"ur \nobreakspace alle \nobreakspace i \end{equation*}

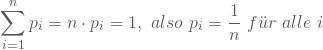
Wie sieht die Verteilung aus?

Deine Wahrscheinlichkeitsfunktion besteht dann grafisch aus einer Reihe von gleich hohen Säulen und die Verteilungsfunktion als kumulierte Wahrscheinlichkeitsfunktion ist eine Treppenkurve mit gleichmäßig hohen Stufen.
Ein Getränkehersteller konzipiert beispielsweise ein neues Erfrischungsgetränk und ist sich über dessen optimalen Anteil von Zitronensaft noch nicht im Klaren. Zur Auswahl stehen vier verschiedene Anteile, 3\%, 5\%, 7\% und 9\%. Da keine verlässlichen Informationen über die Präferenzen der Konsumenten vorliegen, wird, wie oft in der Marktforschung, für die Probandenentscheidungen Gleichverteilung angenommen.

Dein Zufallsexperiment besteht dann darin, welcher Zitronenanteil einem Konsumenten am besten schmeckt; Deine Zufallsvariable X ist seine Wahlentscheidung, mit den möglichen Ausprägungen x_1 = 3\%, x_2 = 5\%, x_3 = 7\% und x_4=9\%. Wegen der angenommenen Gleichverteilung gilt für deren Wahrscheinlichkeiten

    \begin{equation*} p_i = \frac 1 4 = 0,25 \quad f\"ur \nobreakspace alle \nobreakspace i \end{equation*}

Damit hast Du Deine Wahrscheinlichkeits- und Verteilungsfunktionen gegeben:

Variante Zitronenanteil in % Wahrscheinlichkeits-
funktion		 Verteilungsfunktion
i x_i p_i = P(X=x_i) P(X \le x_i)
1 3\% 0,25 0,25
2 5\% 0,25 0,5
3 7\% 0,25 0,75
4 9\% 0,25 1
1

Du kannst beide Funktionen grafisch als

Diskrete Gleichverteilung

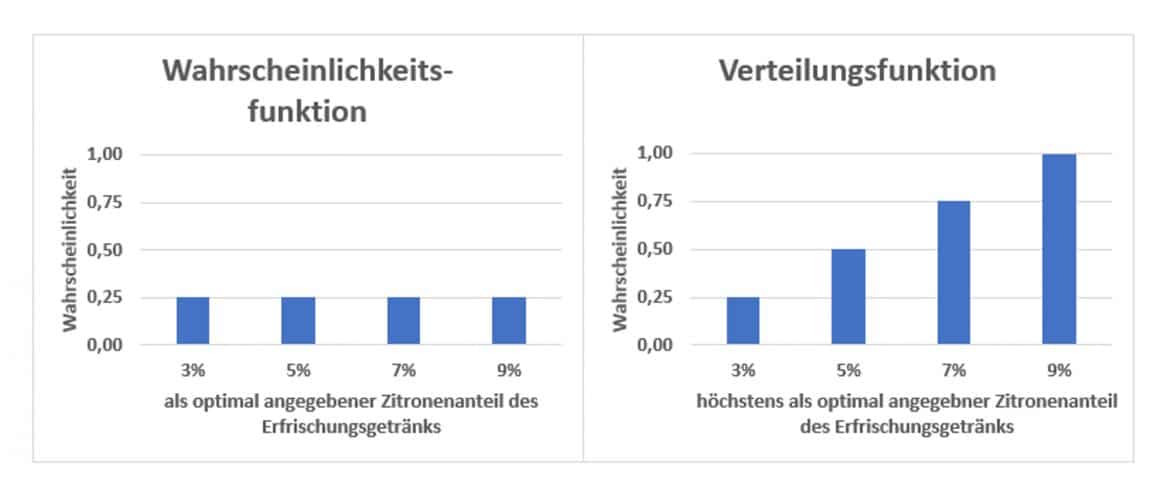
darstellen.

Paramter der Gleichverteilung

Die Parameter der Gleichverteilung erhältst Du zu

    \begin{equation*} \mu = E(X) = \sum_{i=1}^n p_i \cdot x_i = \frac 1 n \cdot \sum_{i=1}^n x_i \end{equation*}

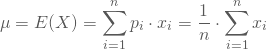
und

    \begin{equation*} \sigma^2 = Var(X) = \sum_{i=1}^n p_i \cdot (x_i - \bar x)^2 = \frac 1 {n^2} \cdot \sum_{i=1}^n (x_i-\bar x)^2 \end{equation*}

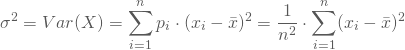
Für Dein Beispiel ergibt sich

Variante Zitronenanteil in % Abweichungen vom Mittel Abweichungsquadrate
i x_i (x_i- \bar x) (x_i- \bar x)^2
1 3\% (0,03 – 0,06) 0,0009
2 5\% (0,05 – 0,06) 0,0001
3 7\% (0,07 – 0,06) 0,0001
4 9\% (0,09 – 0,06) 0,0009
Summe 24\% 0,0020

    \begin{equation*} \mu = \frac 1 4 \cdot (0,03 + 0,05 + 0,07 + 0,09) = 0,06 = 6\% \end{equation*}

und

    \begin{equation*} \sigma^2 = \frac 1 {16} \cdot 0,002 = 0,032 \end{equation*}

Oft führst Du vor Einführung eines neuen Produktes an einer Gruppe von Testpersonen einen Pretest durch. Dabei bietest Du jedem Probanden die Getränkevarianten zum Testen an und bittest ihn anzugeben, welcher Zitronengehalt ihm am besten schmeckt. Dann kannst Du die beobachteten Häufigkeiten mit den angenommenen Wahrscheinlichkeiten vergleichen und mit Hilfe von Tests überprüfen, ob Deine Annahme der Gleichverteilung angesichts der Testergebnisse haltbar ist.