Geometrische Verteilung

Geometrische Verteilung

  • 16. April 2018
  • Posted by: Mika
Keine Kommentare

Stell Dir vor, Du führst ein Bernouilli-Experiment mit der Erfolgswahrscheinlichkeit p wiederholt und zudem unabhängig voneinander durch. Dann möchtest Du wissen, wie oft Du es durchführen musst, um einen ersten Erfolg zu verzeichnen. Die geometrische Verteilung gibt Dir die Wahrscheinlichkeiten an, mit denen Du dazu 1, 2, 3, … Versuche benötigst.

Beispiel für eine geometrische Verteilung

Tobias steht an einer Schießbude und möchte seiner Freundin eine Rose schießen. Leider ist er kein geübter Schütze, und die Wahrscheinlichkeit, mit der sein Schuss trifft, beträgt nur p=0,3. Er möchte nun die Wahrscheinlichkeit für die Anzahl der Schüsse wissen, nach denen er die Rose verschenken kann. Du kannst Dir das Problem anhand eines Baumdiagramms gut veranschaulichen:

Geometrische Verteilung

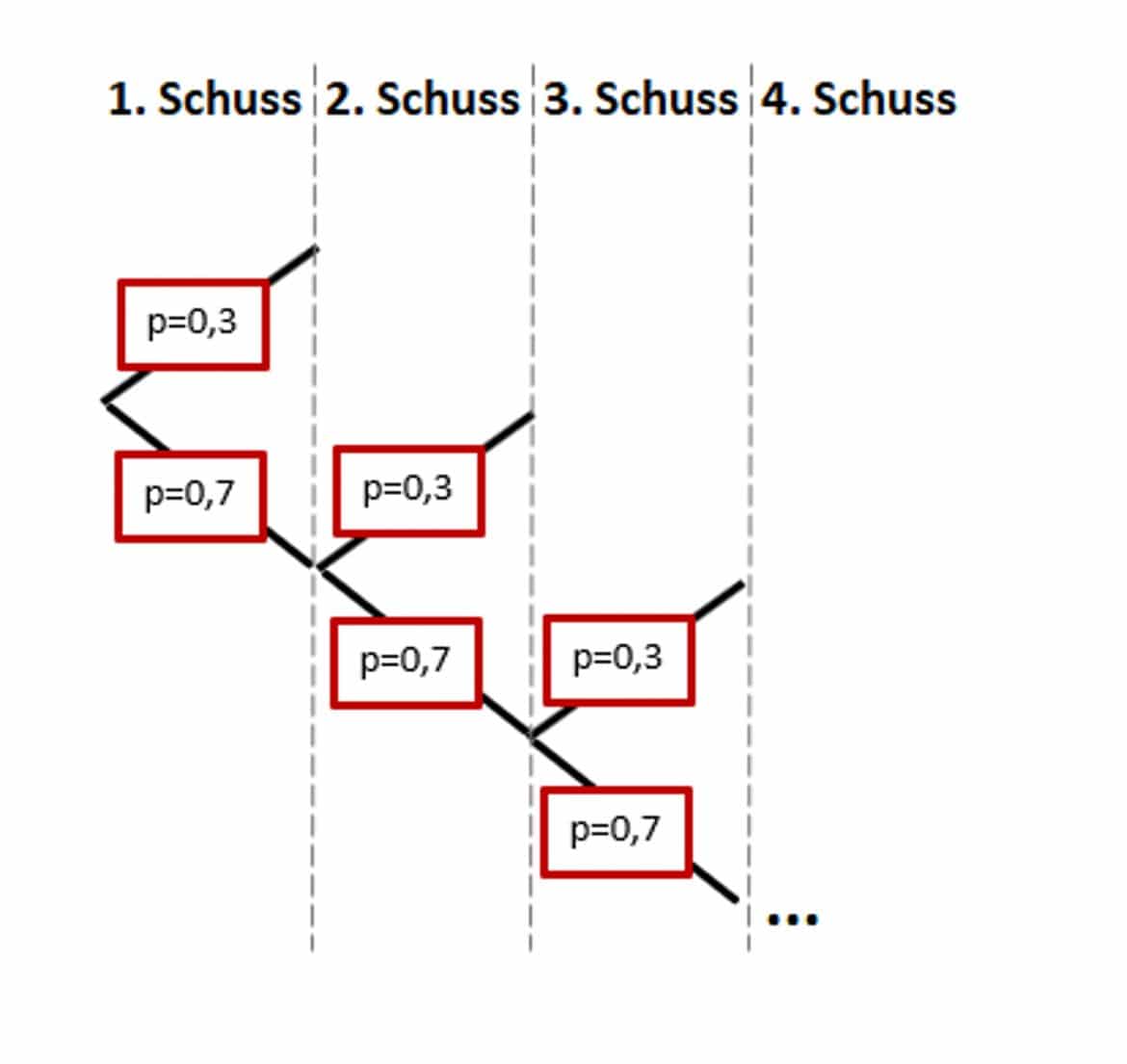
Die Wahrscheinlichkeit beim ersten Schuss zu treffen, beträgt für Tobias laut Aufgabenstellung p=0,3. Für die Wahrscheinlichkeit, beim zweiten Schuss erstmalig zu treffen, muss er beim ersten Versuch danebenschießen: sie ergibt sich daher als Produkt von (1-p) und p.

Damit der dritte Schuss der erste Treffer ist, muss er bei den ersten beiden Schüsse nicht, wohl aber beim dritten Schuss treffen, usw.

k 1 2 3 4 …
P(Treffen beim k-ten Schuss) p (1-p)\cdot p (1-p)^2\cdot p (1-p)^3\cdot p …
in Zahlen 0,3 0,21 0,147 0,1029 …

Berechnng von Wahrscheinlichkeiten

Die Wahrscheinlichkeit, beim k-ten Schuss zum ersten Mal zu treffen, ergibt sich also allgemein als Produkt, der mit (k-1) potenzierten Wahrscheinlichkeit, mit der er nicht trifft, und der Wahrscheinlichkeit, mit der Tobias trifft. Die Wahrscheinlichkeitsfunktion lautet folglich:

    \begin{equation*} P(X=k) = (1-p)^{(k-1)}\cdot p \end{equation*}

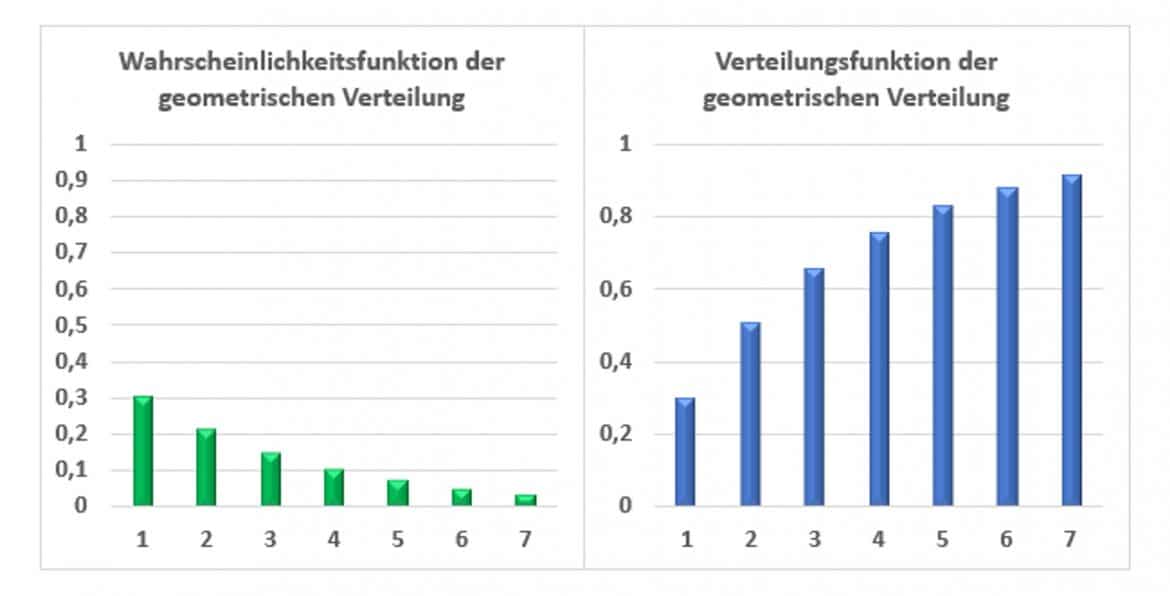
Die Grafik zeigt die Wahrscheinlichkeiten der obigen Tabelle; ihr geometrischer Verlauf erklärt den Namen der Verteilung:
Die Verteilungsfunktion ergibt sich als

    \begin{equation*} F(k) = P(X \le k) = 1 - (1-p)^k \end{equation*}

Geometrischer Verlauf

Ihre Momente erhältst Du zu

    \begin{equation*} \mu = E(X) = \frac 1 p \quad und \quad \sigma^2 = Var(X) = \frac {1-p} {p^2} \end{equation*}

Für Dein Beispiel heißt das:

    \begin{equation*} \mu = \frac 1 {0,3} = 3,33 \quad und \quad \sigma^2 = \frac {1-0,3} {0,3^2}= =7,77 \end{equation*}

Tobias kann im Mittel erwarten, nach 3,33 Versuchen erstmalig zu treffen. Mit der Varianz von 7,77 ist dabei eine hohe Schwankungsbreite gegeben.