Binomialverteilung

Binomialverteilung

  • 16. April 2018
  • Posted by: Mika
Keine Kommentare

Hat Dein Zufallsexperiment nur zwei mögliche Ausgänge x_1 und x_2, die mit den Wahrscheinlichkeiten p und (1-p) auftreten, und führst Du das Experiment unabhängig voneinander n mal durch, dann ist die Häufigkeit des Auftretens des Ausgangs x_1 binomialverteilt. Die Binomialverteilung gehört ferner zur Klasse der diskreten Verteilungen. Da die Binomialverteilung auch für statistische Tests verwendet wird, wie zum Beispiel für den Binomialtest, gehört sie auch zur Kategorie Testverteilung.

Das Servicepersonal eines Restaurants erwägt, das pro Abend erhaltene Trinkgeld nicht mehr aufzuteilen, sondern komplett an den Mitarbeiter zu geben, der die höchste Zahl würfelt. Man fragt Dich als Statistiker nach den Wahrscheinlichkeiten, mit denen ein Mitarbeiter keinmal, einmal, … bzw. fünfmal von fünf Abenden gewinnt.

Das Zufallsexperiment „Würfeln der höchsten Zahl“ hat an jedem Tag die möglichen Ausgänge „Gewinnen“ oder „Verlieren“. Die zugehörige Zufallsvariable X ist also eine Bernouilli-Variable, deren Realisationen Du als 1 und 0 kodieren kannst. Bei vier Mitarbeitern, die mit einem symmetrischen Würfel würfeln, beträgt die Wahrscheinlichkeit, mit der ein Mitarbeiter gewinnt, folglich p=0,25, und die Wahrscheinlichkeit, mit der er verliert, (1-p)=0,75.

Beispiel für ein Experiment

Du betrachtest nun eine Folge von n=5 Tagen. Du beginnst damit, die Wahrscheinlichkeit dafür zu berechnen, dass der Mitarbeiter etwa an den ersten beiden Tagen gewinnt (G) und an den letzten drei Tagen verliert (V): Du erhältst sie durch Multiplikation der einzelnen Wahrscheinlichkeiten, denn das Zufallsexperiment wird unabhängig voneinander fünfmal durchgeführt:

    \begin{equation*} P(G,G,V,V,V) = p \cdot p \cdot (1-p)\cdot (1-p)\cdot (1-p) = 0,25^2\cdot 0,75^3 = 0,0264 \end{equation*}

Für die Beurteilung des neuen Aufteilungsvorschlages ist aber weniger die Wahrscheinlichkeit interessant, genau an den ersten beiden Tagen zu gewinnen, sondern vielmehr diejenige, mit der der Mitarbeiter an zwei beliebigen der fünf Tage gewinnt. Hierfür berechnest Du mit Hilfe der Kombinatorik die Anzahl der Kombinationen aus zwei von fünf Objekten

GGVVV, GVGVV, GVVGV, …,

als den Binomialkoeffizienten

    \begin{equation*} \left(\begin {array} {11} 5 \\2\end{array}\right) = \frac {5!}{2! \cdot 3!}= \frac {5\cdot 4} {1 \cdot 2}=10 \end{equation*}

Wie berechnet man die Wahrscheinlichkeiten?

Für jede dieser 10 möglichen Kombinationen gilt die gleiche oben berechnete Wahrscheinlichkeit von 0,0264. Denn bei der Multiplikation der Eintrittswahrscheinlichkeiten zu den jeweiligen Anordnungen von Experimentausgängen ist es wegen des Kommutativgesetzes egal, in welcher Reihenfolge Du die p- und (1-p)-Werte miteinander multiplizierst.

Daher erhältst Du Deine gewünschte Wahrscheinlichkeit, zweimal bei fünf Durchgängen zu gewinnen, zu

    \begin{equation*} P(zweimal \nobreakspace G, \nobreakspace dreimal \nobreakspace V) = \left(\begin {array} {11} 5 \\2\end{array}\right) \cdot 0,25^2 \cdot 0,75^3 = 10 \cdot 0,0264 = 0,264 \end{equation*}

Allgemein erhältst Du die Wahrscheinlichkeit, bei n unabhängigen Experimentwiederholungen k mal einen bestimmten Experimentausgang zu erhalten, dessen Einzelwahrscheinlichkeit p beträgt, als:

    \begin{equation*} P(k|n;p) = \left(\begin {array} {11} n \\k\end{array}\right) \cdot p^k \cdot (1-p)^{(n-k)}, \quad f\"ur \nobreakspace k=0,..,n \end{equation*}

Für die möglichen Ausgänge Deines obigen Beispiels heißt das:

n=5 Anzahl möglicher Kombinationen Wahrscheinlichkeit für jede einzelne Kombination Wahrscheinlichkeit für k aus 5 Gewinnen
Binomialverteilung
k \left(\begin {array} {11} n \\k\end{array}\right) 0,25^k*0,75^(5-k) P(k;n;p) = \left(\begin {array} {11} n \\k\end{array}\right) \cdot p^k \ cdot (1-p)^{(n-k)}
0 1 0,2373 0,2373
1 5 0,0791 0,3955
2 10 0,0264 0,2637
3 10 0,0088 0,0879
4 5 0,0029 0,0146
5 1 0,0010 0,0010
1,0000

Die Wahrscheinlichkeit, mit der ein Mitarbeiter an keinem der fünf Abende gewinnt, beträgt 0,2373 oder 23,73\%. Dem steht zum Beispiel die Wahrscheinlichkeit von 26,37\% gegenüber, an zwei von fünf Abenden zu gewinnen.

Wahrscheinlichkeitsfunktion der Binomialverteilung

Ausgehend von der Wahrscheinlichkeitsfunktion der Binomialverteilung erhältst Du ihre Verteilungsfunktion durch Kumulieren der Wahrscheinlichkeiten:

    \begin{equation*} P(X \le k|n;p) = \sum_{m=1}^k P(m|n;p) = \sum_{m=1}^k\left(\begin {array} {11} n \\m\end{array}\right) \cdot p^m \cdot (1-p)^{(n-m)}, \quad f\"ur \nobreakspace k,m=0,..,n \end{equation*}

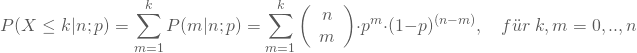
Die Werte dieser Verteilungsfunktion liegen tabelliert vor.

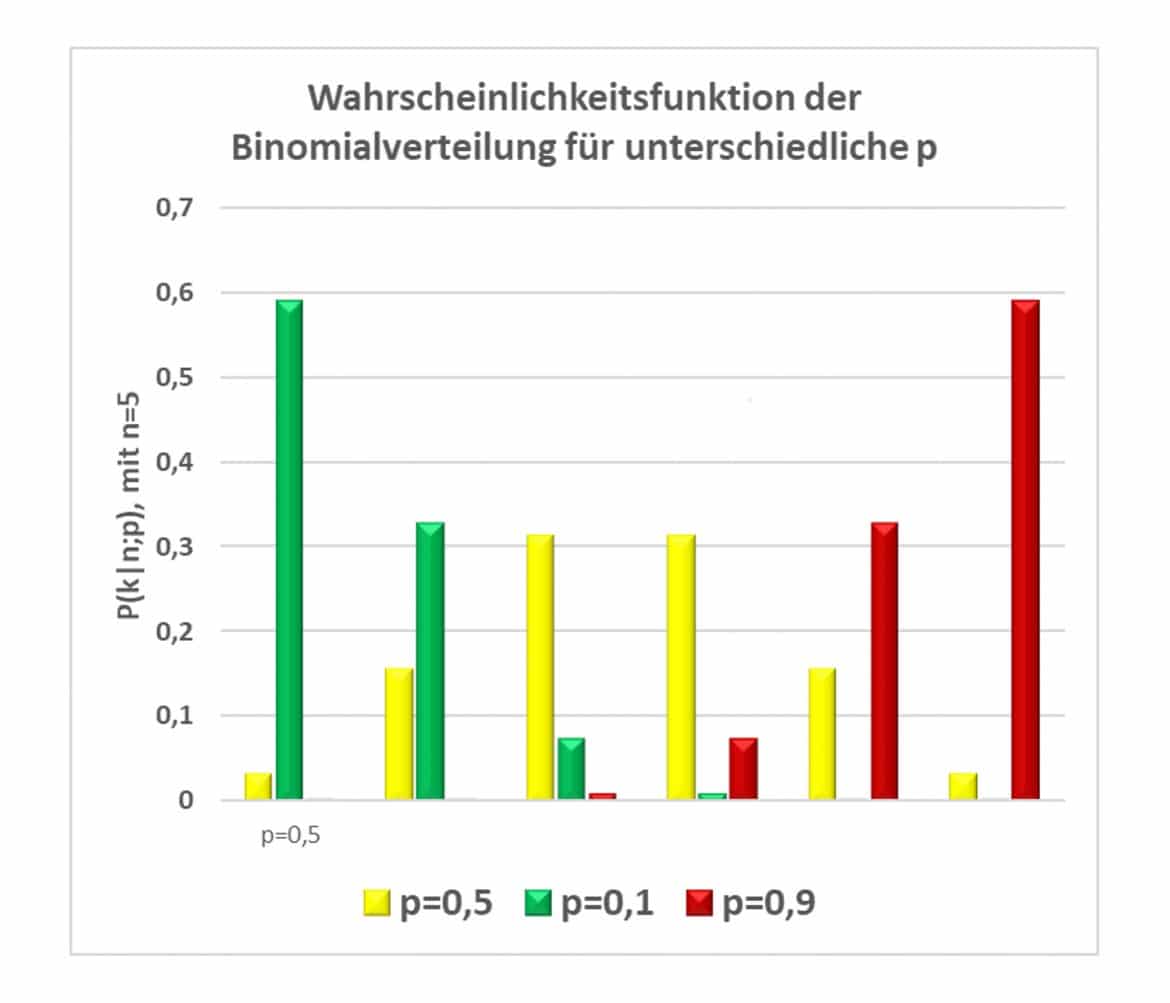
Für p=0,5 ist die Wahrscheinlichkeitsfunktion symmetrisch, für p< 0,5 linkssteil, für p > 0,5 rechtssteil:

binomialverteilung

Erwartungswert und Varianz der Binomialverteilung sind

    \begin{equation*} \mu = n \cdot p \quad und \quad \sigma^2 = n \cdot p \cdot (1-p) \end{equation*}

Für Dein Beispiel heißt das: Mit n\cdot p = 8 \cdot 0,25=2 kannst Du bei n=8 Tagen im Mittel mit zwei Gewinnen rechnen; dabei besteht eine Varianz von

n \cdot p \cdot (1-p) = 8 \cdot 0,25 \cdot 0,75= 1,5.