Bedingte Wahrscheinlichkeit

Bedingte Wahrscheinlichkeit

  • 5. Februar 2018
  • Posted by: Mika
Keine Kommentare

Die bedingte Wahrscheinlichkeit P(A|B) gibt Dir die Wahrscheinlichkeit für das Eintreten von A an, unter der Voraussetzung, dass B gilt.

Stell Dir vor, als Reiseanbieter für junge Leute interessiert Dich das Reiseverhalten deutscher Studenten, von dem Du annimmst, dass es regional recht unterschiedlich ist. Mit A bezeichnest Du das Ereignis: „Reise an die polnische Ostsee“, mit B das Ereignis „Studium in Berlin“.

Bezüglich der Wahrscheinlichkeiten weißt Du:

A: „Reise an die polnische Ostsee“ P(A) = 7\%
B: „Studium in Berlin“ P(B) = 6\%
A \cap B: „Reise an die polnische Ostsee und Studium in Berlin“ P(A \cap B) = 2,1\%

Die Wahrscheinlichkeit, dass ein willkürlich angesprochener Student in Berlin studiert und an die polnische Ostsee fährt, beträgt also 2,1\%.

Um Deine Zielgruppe individuell ansprechen zu können, interessiert Dich aber vielmehr, mit welcher Wahrscheinlichkeit ein in Berlin studierender an die polnische Ostsee fährt, also die Wahrscheinlichkeit von A, wenn B bereits eingetreten ist. Aufgrund der unmittelbaren Nähe von Berlin zu Polen sollte diese Wahrscheinlichkeit deutlich höher sein.

Berechnung von bedingten Wahrscheinlichkeiten

Du berechnest die bedingte Wahrscheinlichkeit als

    \begin{equation*} P(A | B) = \frac {P(A \cap B)} {P(B) } = \frac {2,1 \%}{6 \%}= 0,35 \% \end{equation*}

35% der Berliner Studenten reisen also an die polnische Ostsee. Hier könnte es sich für Dein Unternehmen lohnen, gezielte Verkaufsförderung zu betreiben.

Generell lässt sich die Idee der bedingten Wahrscheinlichkeit anschaulich anhand eines Baumdiagramms darstellen:

Bedingte Wahrscheinlichkeiten

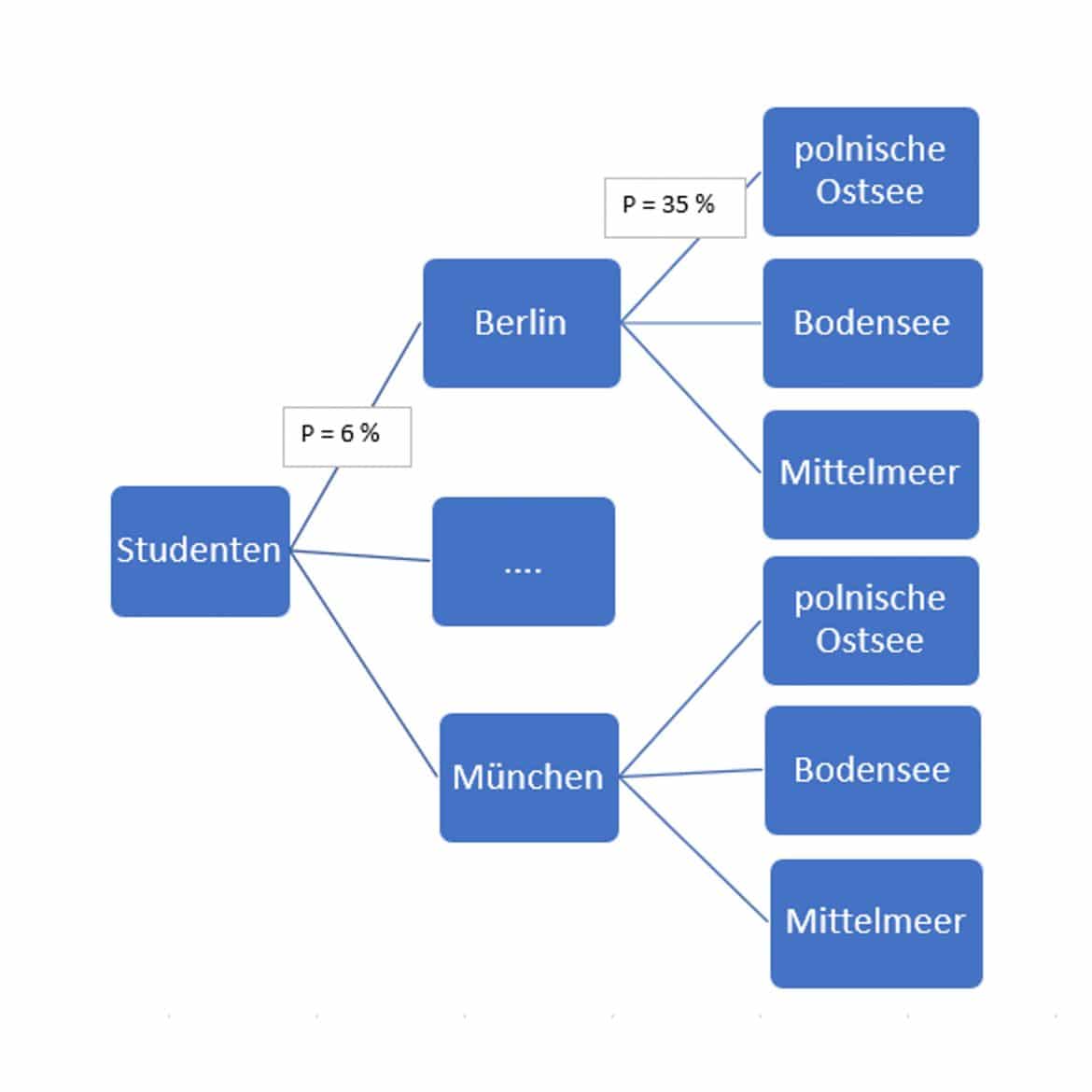
Für einen willkürlich ausgewählten Studenten beträgt die Wahrscheinlichkeit, dass er in Berlin studiert, 6\%. Ein Student, der in Berlin studiert, reist mit einer Wahrscheinlichkeit von 35\% an die polnische Ostsee.

Die Wahrscheinlichkeiten aller von einem Punkt im Baumdiagramm direkt ausgehenden Ereignisse addieren sich immer zu Eins.