Wahrscheinlichkeiten

Wahrscheinlichkeiten

  • 5. Februar 2018
  • Posted by: Mika
Keine Kommentare

Die Wahrscheinlichkeit P(A) für ein zufälliges Ereignis A liefert Dir ein Maß für die Sicherheit seines Eintretens. Sie wird im Intervall [0;1] angegeben; je größer P(A) ist, umso sicherer kannst Du also das Eintreten von A erwarten. Ein sicheres Ereignis besitzt die Wahrscheinlichkeit 1, ein unmögliches Ereignis dagegen die Wahrscheinlichkeit 0.

Beim symmetrischen Würfel zum Beispiel besitzt jede Augenzahl die gleiche Wahrscheinlichkeit geworfen zu werden, nämlich \frac 1 6 = 0,1667. Betrachtest Du etwa das Ereignis, eine Augenzahl kleiner als 5 zu werfen, so ist dieses mit den Augenzahlen 1 bis 4 realisierbar; seine Wahrscheinlichkeit beträgt dann \frac 4 6 = frac 2 3 = 0,667.

Dein sicheres Ereignis, das mit der Wahrscheinlichkeit von 1 eintritt, wäre es, eine Augenzahl kleiner als 7 zu erzielen; ein unmögliches Ereignis mit der Wahrscheinlichkeit 0 etwa eine Augenzahl von 8 zu erreichen.

Wie definiert man Wahrscheinlichkeiten formal?

Formal ist das Wahrscheinlichkeitsmaß P eine Zuordnung des Ergebnisraumes \Omega, also der möglichen Ereignisse A_1 bis A_n eines Zufallsexperimentes, auf reelle Zahlen im Intervall [0;1],

    \begin{equation*} P: \Omega = \{A_1, A_2, ..., A_n\} \to [0;1] \end{equation*}

für die gilt:

Die Wahrscheinlichkeit für jedes mögliche Ereignis liegt zwischen Null und Eins.

    \begin{equation*} 0 \le P(A_i) \le 1 \quad f\"ur \nobreakspace alle \nobreakspace i \end{equation*}

Die Wahrscheinlichkeit dafür, dass ein beliebiges der möglichen Ereignisse eintritt, beträgt eins.

    \begin{equation*} P(\Omega) = 1, \quad wobei \nobreakspace \Omega \nobreakspace der \nobreakspace Ergebnisraum \nobreakspace ist \end{equation*}

Die Wahrscheinlichkeit der Vereinigungsmenge von sich gegenseitig ausschließenden Ereignissen ist gleich der Summe der Wahrscheinlichkeiten dieser Ereignisse.

    \begin{equation*} P(\bigcup_{i=1}^m A_i) = \sum_{i=1}^m P(A_i), \quad mit \quad A_i \cap A_j = \emptyset \quad f\"ur \nobreakspace beliebige \nobreakspace i,j \quad und \quad m \le n \end{equation*}

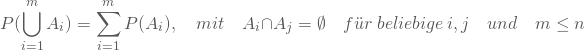
Beim symmetrischen Würfel wurden die ersten beiden Eigenschaften oben bereits gezeigt.

Die Wahrscheinlichkeit, dass die Vereinigung aller sich gegenseitig ausschließender Ereignisse eintritt, ergibt sich als Summe der Einzelwahrscheinlichkeiten:

    \begin{equation*} P(\bigcup_{i=1}^6 A_i) = \sum_{i=1}^6 P(A_i) = 6 \cdot \frac 1 6 = 1 \end{equation*}

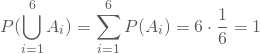
Rechenregeln für Wahrscheinlichkeiten

Aus diesen Eigenschaften lassen sich die folgenden Rechenregeln für Wahrscheinlichkeiten ableiten, die Du mithilfe von Venn-Diagrammen leicht veranschaulichen kannst:

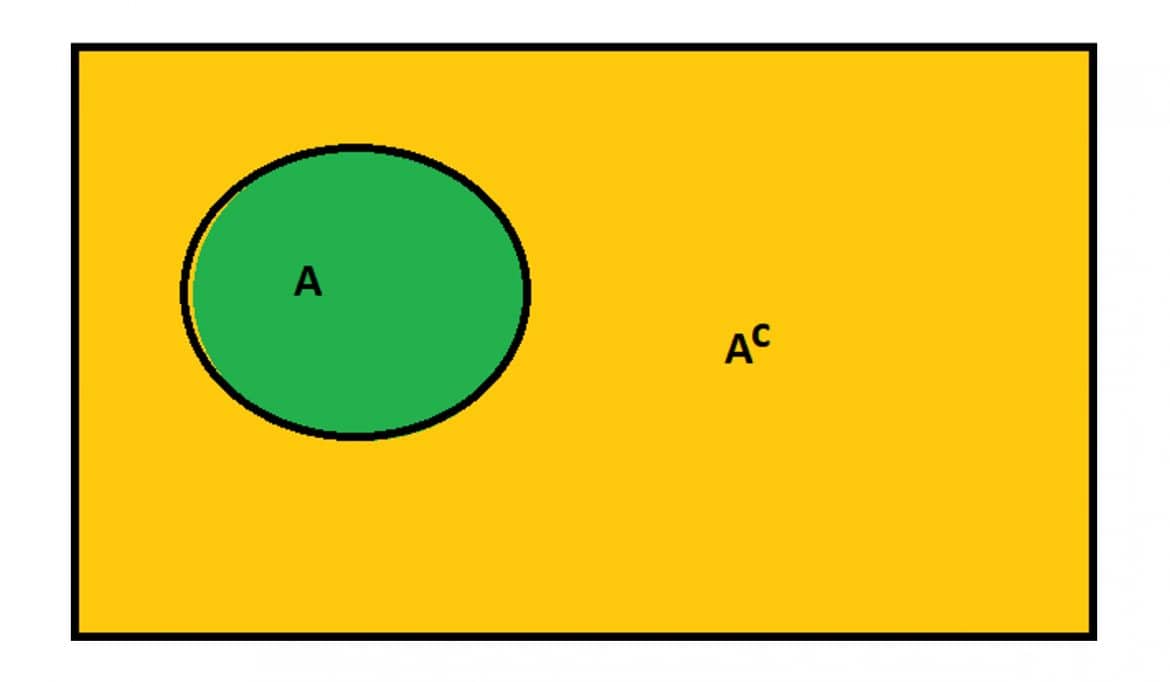
Gegenwahrscheinlichkeit

Wenn A^c das Gegenereignis zu A ist, und P(A) die Wahrscheinlichkeit, mit der das Ereignis A eintritt, so beträgt die Wahrscheinlichkeit, mit der A nicht eintritt, genau (1-P(A))

Gegenereignis

    \begin{equation*} P(A^c) = 1 - P(A) \end{equation*}

Wenn die Meteorologen melden, dass die Regenwahrscheinlichkeit für morgen 30\% beträgt, kennst Du damit auch die Wahrscheinlichkeit, mit der es trocken bleibt; sie beträgt nämlich 100\%-30\% = 70\%.

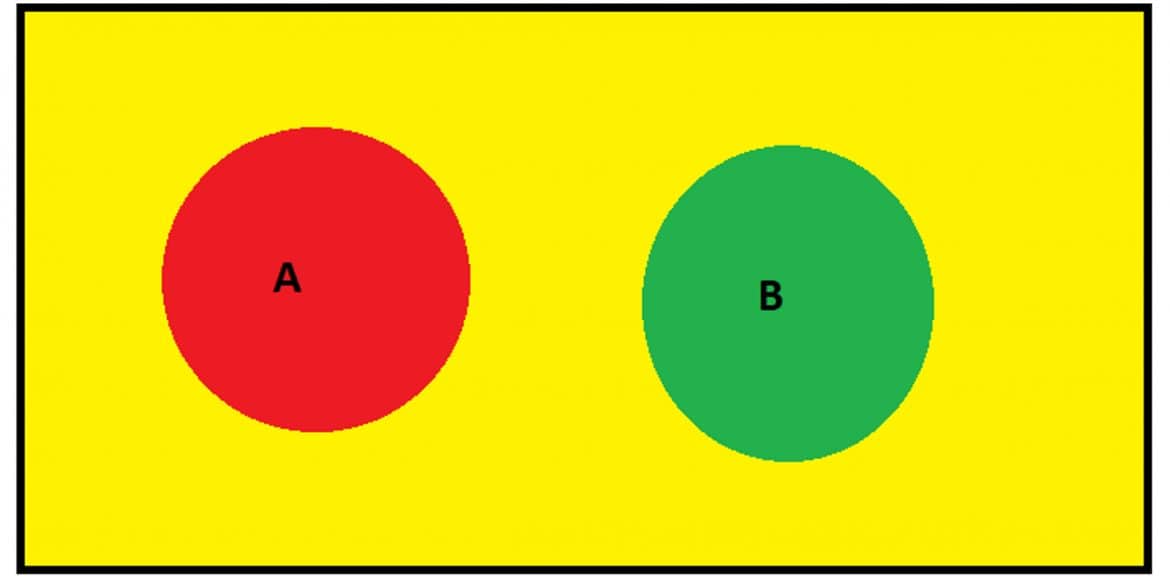
Wahrscheinlichkeit für zwei sich gegenseitig ausschließende Ereignisse

Wenn A und B zwei Ereignisse sind, die sich gegenseitig ausschließen (disjunkte Ereignisse), kannst Du die Wahrscheinlichkeit, mit der ihre Vereinigungsmenge eintritt, als Summe der Einzelwahrscheinlichkeiten berechnen.

Disjunkte Ereignisse

    \begin{equation*} P(A \cup B) = P(A) + P(B), \quad wenn \nobreakspace A \nobreakspace und \nobreakspace B \nobreakspace disjunkt \end{equation*}

Die Augenzahlen beim Würfeln sind disjunkte Ereignisse, Du kannst entweder eine 1 oder eine 2 Würfeln, aber nicht beides zusammen. Daher gilt für die Wahrscheinlichkeit, einen Augenzahl (AZ) kleiner als 3 zu würfeln:

    \begin{equation*} P(AZ < 3) = P((AZ=1) \cup (AZ = 2)) = P[(AZ=1) + P(AZ=2)]= \frac 1 6 + \frac 1 6 = \frac 1 3 \end{equation*}

Wahrscheinlichkeit für zwei beliebige Ereignisse

Wenn A und B sich nicht gegenseitig ausschließen, sondern auch gemeinsam auftreten können, berechnest Du die Wahrscheinlichkeit ihrer Vereinigungsmenge als Summe der Einzelwahrscheinlichkeiten abzüglich der Wahrscheinlichkeit ihrer Schnittmenge, um Doppelzählungen zu vermeiden.

Nicht disjunkte Ereignisse

    \begin{equation*} P(A \cup B) = P(A) + P(B) - P(A \cap B), \quad f\"ur \nobreakspace beliebige \nobreakspace A \nobreakspace und \nobreakspace B \end{equation*}

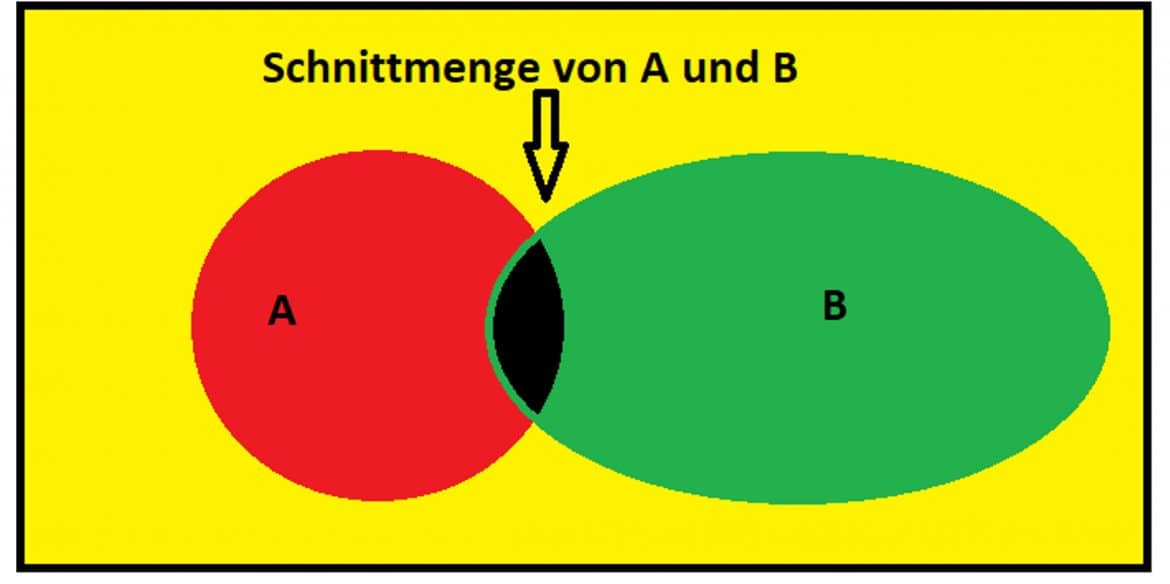
Du weißt, dass die Laune eines Deiner Kommilitonen sowohl vom guten Wetter, als auch vom Ergebnis seiner Fußballmannschaft abhängig ist. Du bezeichnest mit A das Ereignis: „die Sonne scheint“, das mit einer Wahrscheinlichkeit P(A)=60\% auftritt, und mit B das Ereignis: „seine Fußballmannschaft gewinnt“, mit einer Wahrscheinlichkeit von P(B)=40\%. Beide Ereignisse können auch gemeinsam, als Schnittmenge von A und B, auftreten: (A \cap B): „die Sonne scheint und die Fußballmannschaft gewinnt“, mit einer Wahrscheinlichkeit von P(A \cap B) = 20\%.

Die Wahrscheinlichkeit, dass entweder die Sonne scheint oder die Fußballmannschaft gewinnt, die Vereinigungsmenge von A und B also, erhältst Du dann als:

    \begin{equation*} P(A \cup B) = P(A) + P(B) - P(A \cap B) = 60\% + 40\% -20\% = 80\% \end{equation*}

Du kannst also mit einer Wahrscheinlichkeit von 80\% annehmen, dass Dein Kommilitone einigermaßen gut gelaunt ist.
Stochastische Unabhängigkeit: Zwei Ereignisse heißen stochastisch unabhängig, wenn sich die Wahrscheinlichkeit für das Eintreten ihrer Schnittmenge als Produkt ihrer Einzelwahrscheinlichkeiten zerlegen lässt.

    \begin{equation*} P(A \cap B) = P(A) \cdot P(B) \end{equation*}

Für das obige Beispiel ergibt sich:

    \begin{equation*} P(A) \cdot P(B) = 0,6 \cdot 0,4=0,24 \ne 0,2 = P(A \cap B) \end{equation*}

Die Ereignisse A und B sind also nicht stochastisch unabhängig. Die Leistung des Teams scheint also abhängig vom Wetter zu sein.