Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Markov-Kette
- 25. April 2018
- Posted by: Mika
Hat Dein stochastischer Prozess ein „kurzes Gedächtnis“ bzw., präzise ausgedrückt, ist für die Verteilung von X(t) ausschließlich die vorherige Realisation von X(t-1) relevant und alle davor liegenden Werte besitzen keinen Einfluss, so ist Dein Prozess ein Markov-Prozess.
Die Verteilungsfunktion von X(t) wird dann nicht von weiter in der Vergangenheit liegenden Realisationen verändert:
![]()
Handelt es sich um einen zeitdiskreten Prozess, wenn also X(t) nur abzählbar viele Werte annehmen kann, so heißt Dein Prozess Markov-Kette.
Stell Dir vor, ein Spieler besitzt ein Anfangskapital ![]() von 30 Euro. Er spielt im Casino mit einem idealen Würfel nach den folgenden Spielregeln:
von 30 Euro. Er spielt im Casino mit einem idealen Würfel nach den folgenden Spielregeln:
- würfelt er eine Eins, Zwei oder Drei, so zahlt er 10 € an die Bank.
- würfelt er die Vier, erhält niemand eine Auszahlung, und
- wirft er fünf oder sechs Augen, so zahlt ihm die Bank 10 € aus.
Wegen des idealen Würfels, bei dem die Wahrscheinlichkeit für jede Augenzahl ![]() beträgt, kannst Du die Wahrscheinlichkeiten für die interessanten Ereignisse bestimmen:
beträgt, kannst Du die Wahrscheinlichkeiten für die interessanten Ereignisse bestimmen:
![]()
![]()
![]()
Vor Spielbeginn legt der Spieler noch die folgenden Ausstiegsregeln fest: Er beendet das Spiel, wenn sein Kapital auf 10 Euro geschmolzen oder auf 50 Euro angestiegen ist.
Du kannst die Höhe seines Kapitals jetzt als stochastischen Prozess X(t) betrachten, mit X(0)=30, der sich bei jedem Wurf t= 0,1,… entsprechend der Spielregeln erhöht, gleichbleibt oder reduziert: Mögliche Prozessverläufe in den ersten Runden sind in der Grafik dargestellt:

Das Anfangskapital in Periode t=0 ist mit X(0)=30 bekannt. Für Periode t=1 gibt es drei mögliche Kapitalbeträge, die mit den bekannten Wahrscheinlichkeiten eintreten. Der Spieler würfelt in t=1; entsprechend der geworfenen Augenzahl erhält er eine Auszahlung, muss selbst bezahlen oder sein Kapital bleibt gleich. Der gleiche Ablauf erfolgt in t=2. Dadurch ergeben sich die möglichen Kapitalbestände X(2).
In der Grafik kannst Du erkennen, dass sich bei der Variante X(2)=30 drei Zweige treffen: Dieser Kapitalbestand kann sich aus dem Anfangskapital entweder durch Zahlung von 10 € in der ersten Runde und Erhalt von 10 Euro in der zweiten Runde oder durch Erhalt von 10 € in der ersten Runde und Zahlung von 10 € in der zweiten Runde oder durch zweimaliges Würfeln der Vier, ohne irgendeine Auszahlung also, ergeben.
Wie aber die 30 € zustande gekommen sind, spielt für den Fortgang des Spiels keine Rolle: ausgehend von X(2)=30 € gibt es drei mögliche Spielausgänge.
Da für die Erwartungen von X(t) also nur die Realisation x(t-1) relevant ist, hast Du eine Markov-Kette gegeben. Diese stellst Du üblicherweise durch ein Prozessdiagramm dar, das die möglichen (abzählbar vielen) Zustände ![]() und die Übergangswahrscheinlichkeiten von einem Zustand in den anderen enthält: In Deinem Beispiel hast Du fünf mögliche Zustände gegeben:
und die Übergangswahrscheinlichkeiten von einem Zustand in den anderen enthält: In Deinem Beispiel hast Du fünf mögliche Zustände gegeben:
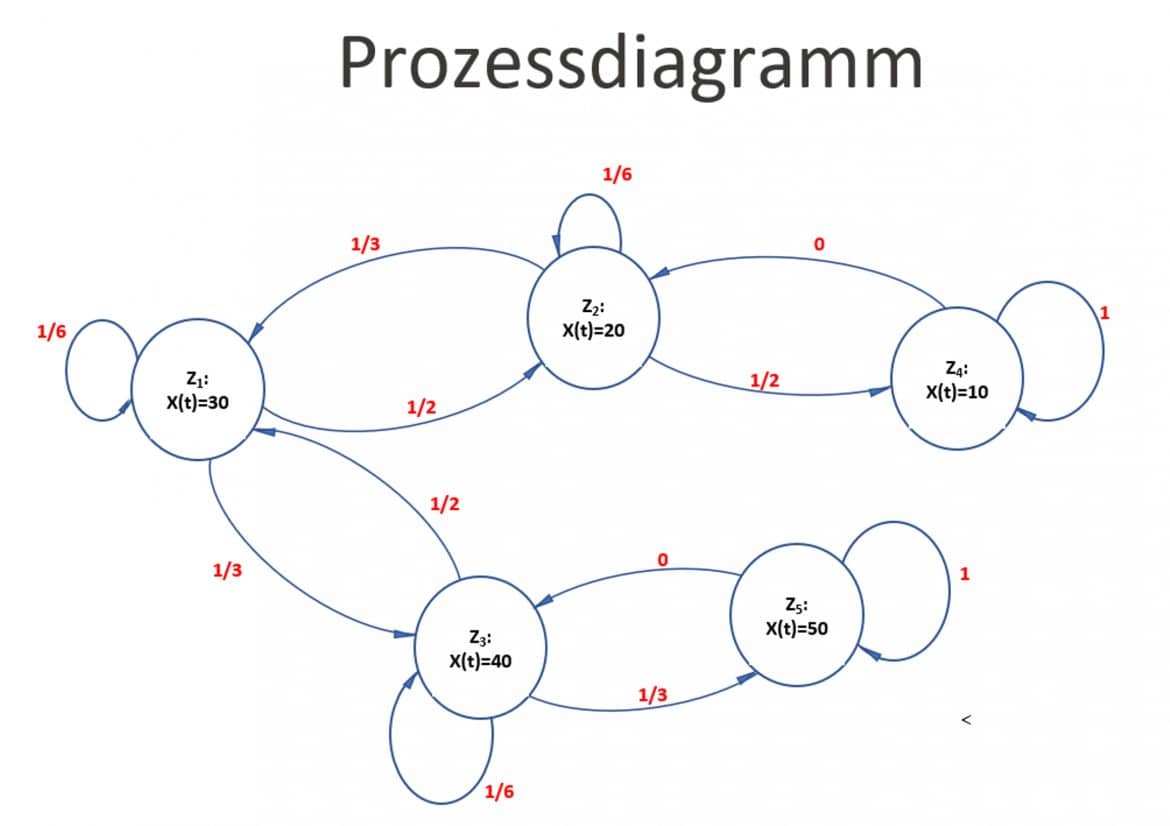
Die verschiedenen Zustände sind mit gerichteten Pfeilen versehen, die in roter Schrift die Übergangswahrscheinlichkeiten von einem Zustand in den anderen aufzeigen. Befindest Du Dich etwa im Zustand ![]() mit X(t)=20 €,
mit X(t)=20 €,
- so führt ein Pfeil zu
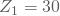 ; ein Gewinn von 10€ und der Übergang zu
; ein Gewinn von 10€ und der Übergang zu  tritt mit einer Wahrscheinlichkeit von
tritt mit einer Wahrscheinlichkeit von  ein;
ein; - ein weiterer Pfeil führt zu Zustand
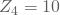 ; einen Verlust von 10 € und den Übergang zu
; einen Verlust von 10 € und den Übergang zu 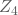 erleidest Du mit einer Übergangswahrscheinlichkeit von
erleidest Du mit einer Übergangswahrscheinlichkeit von  ;
; - ein dritter Preil führt von
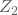 zu
zu 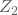 und zeigt die Bleibewahrscheinlichkeit in Höhe von
und zeigt die Bleibewahrscheinlichkeit in Höhe von 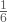 an.
an.
Um das Prozessdiagramm rechentechnisch besser handhaben zu können, fasst Du es in einer Übergangsmatrix zusammen, bei der die Zeilen die Zustände angeben, in die gewechselt wird und die Spalten die Zustände bezeichnen, aus denen gewechselt wird:
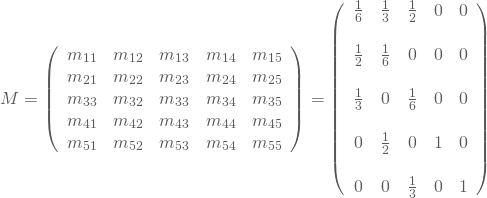
![]() gibt Dir die Wahrscheinlichkeit an, mit der sich der Spieler aus dem Zustand
gibt Dir die Wahrscheinlichkeit an, mit der sich der Spieler aus dem Zustand ![]() in den Zustand
in den Zustand ![]() begibt: Die Wahrscheinlichkeit beträgt
begibt: Die Wahrscheinlichkeit beträgt ![]() .
.
Bezeichnest Du jetzt mit ![]() den Spaltenvektor der Wahrscheinlichkeiten, mit denen der Zustand i im Zeitpunkt t erreicht wird,
den Spaltenvektor der Wahrscheinlichkeiten, mit denen der Zustand i im Zeitpunkt t erreicht wird,
![]()
so gilt für t=0 mit bekanntem Anfangskapital:
Mit Sicherheit ist in t=0 der Zustand 1 eingetreten.
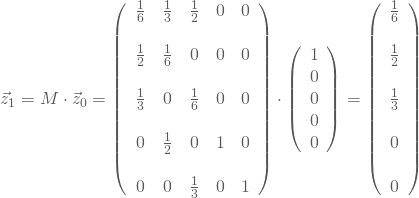
Die Wahrscheinlichkeiten ![]() im Zeitpunkt t=1 erhältst Du durch Multiplikation von M und
im Zeitpunkt t=1 erhältst Du durch Multiplikation von M und ![]() :
:
Allgemein erhältst Du die Wahrscheinlichkeiten ![]() , mit denen der Zustand
, mit denen der Zustand ![]() i in der Periode t erreicht wird, durch Multiplikation der Matrix der Übergangswahrscheinlichkeiten mit dem Vektor
i in der Periode t erreicht wird, durch Multiplikation der Matrix der Übergangswahrscheinlichkeiten mit dem Vektor ![]() der Vorperiode:
der Vorperiode:
![]()
Für ausgewählte Zeitpunkte t zeigt Dir die Tabelle diese Wahrscheinlichkeiten für Dein Beispiel:
| t | 0 | 1 | 2 | … | 5 | … | 10 | … | 15 |
| 1,00 | 0,17 | 0,36 | … | 0,11 | … | 0,03 | … | 0,01 | |
| – | 0,50 | 0,17 | 0,10 | 0,02 | 0,01 | ||||
| – | 0,33 | 0,11 | 0,07 | 0,01 | 0,00 | ||||
| – | – | 0,25 | 0,50 | 0,65 | 0,68 | ||||
| – | – | 0,11 | 0,22 | 0,29 | 0,30 |
Die letzte Spalte gibt also die Wahrscheinlichkeiten an, mit denen die Zustände ![]() bis
bis ![]() nach der 15. Runde erreicht werden: die ersten drei (gemäßigten Zustände) sind dann sehr unwahrscheinlich; die Zahl 0,68 in der zweitunterste Zeile besagt, dass der Spieler nach der 15. Runde mit einer Wahrscheinlichkeit von
nach der 15. Runde erreicht werden: die ersten drei (gemäßigten Zustände) sind dann sehr unwahrscheinlich; die Zahl 0,68 in der zweitunterste Zeile besagt, dass der Spieler nach der 15. Runde mit einer Wahrscheinlichkeit von ![]() im Zustand
im Zustand ![]() ist, also mit einem Restkapital von 10 € ausgestiegen ist; mit einer Wahrscheinlichkeit von
ist, also mit einem Restkapital von 10 € ausgestiegen ist; mit einer Wahrscheinlichkeit von ![]() besitzt er dann ein Restkapital von 50 €.
besitzt er dann ein Restkapital von 50 €.
Markov-Ketten können in sehr unterschiedlichen Bereichen eingesetzt werden, beispielsweise
- in der Warteschlangentheorie, um die Wahrscheinlichkeiten für die Anzahl der in einer Schlange stehenden Kunden zu ermitteln;
- in der der Finanztheorie, zur Modellierung von Aktenkursentwicklungen;
- in der Versicherungsmathematik etwa zur Modellierung von Invaliditätsrisiken sowie
- im Qualitätsmanagement, zur Quantifizierung der Ausfallwahrscheinlichkeiten von Systemen.
