Stochastische Prozesse

Hast Du eine Folge von Zufallsvariablen X(t) gegeben, die von einem sich ändernden Parameter t abhängen, so sprichst Du von einem stochastischen Prozess. Generell kann t einen beliebigen Parameterraum durchlaufen, wird aber häufig als Zeit interpretiert. Daher werden stochastische Prozesse auch als Dynamisierung der Wahrscheinlichkeitstheorie bezeichnet.

Formal beschreibst Du einen stochastischen Prozess als

   

X(t) kann beispielsweise den Kurswert einer Aktie zum Zeitpunkt t innerhalb eines Zeitraums T darstellen. Du kannst dann folgende Situationen unterscheiden und die stochastischen Prozesse danach einteilen:

• Diskrete / stetige Zeitbetrachtung
  Interessieren Dich beispielsweise die täglichen Börsenschlusskurse, so hast Du für jeden Tag t einen Kurswert X(t) gegeben. T steht dann für eine diskrete Menge von Zeitpunkten und der Prozess heißt zeitdiskret.
  Ist T dagegen ein Intervall und interessiert Dich prinzipiell jeder Wert der Aktie innerhalb dieses Intervalls, so sprichst Du von zeitstetigen Prozessen.
• Diskrete / stetige Wertemenge
  Unterstellst Du für Deinen Prozess, dass X(t) nur abzählbar viele verschiedene Werte annehmen kann, so heißt der Prozess wertediskret; im Fall Deines Aktienkurses ist das der Fall, wenn Du als kleinste mögliche Änderung beispielsweise einen Cent annimmst. Unterstellst Du dagegen einen stetigen Verlauf von X(t), bei dem der Prozess jeden beliebigen Wert innerhalb eines Intervalls annehmen kann, so heißt der Prozess wertestetig.
• Stochastische Abhängigkeiten
  Die stochastischen Abhängigkeiten Deines Prozesses bestimmen die Erwartungen, die Du bei Kenntnis der Realisationen bis (t-1) für Deinen Prozess X(t) in t hast. Danach kannst Du die folgenden speziellen Prozesse unterscheiden:
  • Beim Markov-Prozess ist die Verteilung von X(t) im Zeitpunkt t nur abhängig von seiner Realisation im Zeitpunkt (t-1); alle vorherigen Realisationen haben keine Bedeutung. Du kannst auch von einem Prozess mit „kurzem Gedächtnis“ sprechen.

  • Ein Martingal ist ein stochastischer Prozess, bei dem der Erwartungswert von X(t) gerade seiner Realisation in (t-1) entspricht:

       

    Ist X(t) wieder Dein unbekannter Aktienkurs im Zeitpunkt t und ist 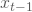Dein Kurswert in der Vorperiode, so gleichen sich die erwarteten Verluste und Wertsteigerungen aus und Du erwartest im Mittel keine Änderungen. Du kannst in diesem Zusammenhang auch von fairem Spiel sprechen.

    Ist der Erwartungswert von X(t) größer als die bekannte Realisation in (t-1), erwartest Du also Kursgewinne, so ist Dein Kursverlauf ein Submartingal; liegt Dein Erwartungswert in t unter der Realisation in (t-1), erwartest Du also Kursverluste, so heißt Dein Prozess Supermartingal.

Gegenüber der Zeitreihenanalyse, die die Realisationen der X(t) durch Modelle zu erklären sucht, betrachtest Du bei den stochastischen Prozessen das dynamische Verhalten der Zufallsvariablen im Zeitablauf.