Varianz

Varianz

  • 5. Februar 2018
  • Posted by: Mika
Keine Kommentare

Die Varianz oder Streuung einer Zufallsvariablen gibt Dir die durchschnittliche quadrierte Abweichung Deiner Zufallsvariablen von ihrem Erwartungswert an. Während der Erwartungswert ein Maß für die Lage bzw. den Schwerpunkt der Verteilung darstellt, ist die Varianz \sigma^2 ein Maß für die Schwankungsbreite Deiner Zufallsvariablen und Du erhältst durch sie weitere Informationen über die Verteilung.

    \begin{equation*} \sigma^2 = Var (X) = E[X-E(X)]^2 = E[X-\mu]^2 \end{equation*}

Die Varianz ist durch die Quadrierung der Abweichungen folglich immer größer oder gleich Null.

Ihre Wurzel, die Standardabweichung \sigma, kannst Du als mittlere Abweichung der Zufallsvariablen vom Erwartungswert interpretieren. Sie spielt in der Schätz- und Testtheorie eine wichtige Rolle.

In der Grafik siehst Du zwei Verteilungen, die den gleichen Erwartungswert aber unterschiedliche Varianzen besitzen: Die Varianz der roten Verteilung ist zweimal so groß wie die der blauen.

Varianz

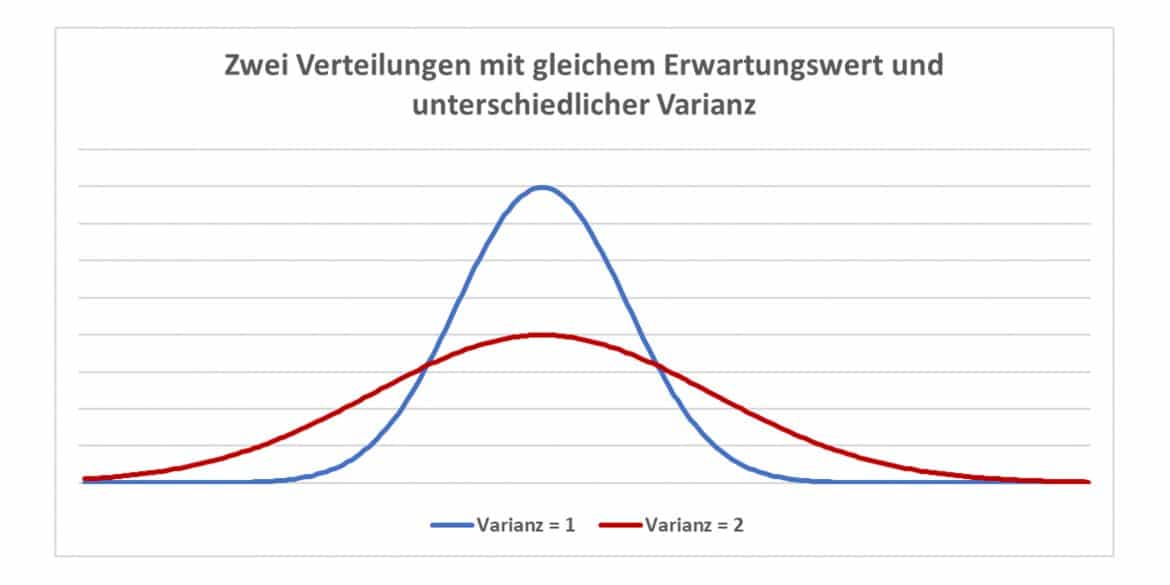
Stell Dir beispielsweise vor, Du vergleichst zwei Aktien, in die Du eventuell investieren möchtest. Dann interessiert Dich nicht nur der erwartete Kurswert (Erwartungswert), sondern auch, wie stark diese Aktie schwankt: Denn es macht auf jeden Fall einen Unterschied, ob Du den zukünftigen Kurs im Bereich [90€;110€] mit geringer Streuung oder im Bereich [50€;150€] mit deutlich größerer Streuung erwartest.

Bei der Varianzberechnung unterscheidest du zwischen diskreten und stetigen Zufallsvariablen:

Varianz bei diskreten Zufallsvariablen

Für jede mögliche Ausprägung x_i, die Deine Zufallsvariable annehmen kann, quadrierst Du zuerst deren Differenz zum Erwartungswert, multiplizierst mit der zugehörigen Wahrscheinlichkeit und bildest den Mittelwert dieser Werte:

    \begin{equation*} \sigma^2 = Var(X) = \sum_{i=1}^n p_i \cdot (x_i-\mu)^2 \end{equation*}

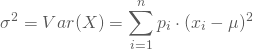
Für eine Aktie erwartest Du zum Beispiel zu Beginn des nächsten Jahres fünf mögliche Kurswerte x_i, die mit den Wahrscheinlichkeiten p_i eintreten werden:

lfd. Nr. i x_i p_i x_i\cdot p_i (x_i-\mu)^2 p_i \cdot (x_i-\mu)^2
1 90 0,1 9 576 57,6
2 95 0,1 9,5 361 36,1
3 100 0,2 20 196 39,2
4 105 0,3 31,5 81 24,3
5 110 0,4 44 16 6,4
\mu =114 \sigma^2 =163,6

 

Aus den Werten der zweiten und dritten Tabellenspalte bestimmst Du zuerst den Erwartungswert \mu, um dann die Varianz \sigma^2 zu berechnen.

Varianz bei stetigen Zufallsvariablen

Im Falle von stetigen Zufallsvariablen ist die Wahrscheinlichkeit, mit der sie einen bestimmten Wert annehmen, immer gleich Null. Anstelle der Wahrscheinlichkeiten besitzt eine stetige Zufallsvariable außerdem eine Dichtefunktion f(x). Du erhältst ihre Varianz dann als Integral über das Produkt zwischen quadrierter Differenz (x-\mu)^2 und der Dichtefunktion:

    \begin{equation*} \sigma^2 = Var(X) = \int_{-\infty}^{\infty}\quad (x-\mu)^2 \cdot f(x) dx \end{equation*}

Wenn X und Y Zufallsvariablen und a und b Konstante sind, hast Du als Rechenregeln für die Varianz gegeben:

    \begin{equation*} Var(a\cdot X + b \cdot Y) = a^2 \cdot Var(X) + b^2 \cdot Var(Y)+2ab*Cov(X,Y) \end{equation*}

Für den Fall von a=b=1 ergibt sich der Spezialfall:

    \begin{equation*} Var(X + Y) = Var(X) + Var(Y)+Cov(X,Y) \end{equation*}

Für den Fall, dass X und Y stochastisch unabhängig sind, gilt sogar

    \begin{equation*} Var(X + Y) = Var(X) + Var(Y). \end{equation*}

Es gilt zudem der Verschiebungssatz, nach dem Du die Varianz als Funktion von Erwartungswerten schreiben kannst:

    \begin{equation*} Var(X) = E[X-E(X)]^2 = E(X^2) - [E(X)]^2 \end{equation*}

Von der Varianz \sigma^2 = Var(X) Deiner Zufallsvariablen musst Du die Stichprobenvarianz s^2 unterscheiden. Im Gegensatz zur theoretischen Varianz wird sie in vielen statistischen Untersuchungen aus dem Datenmaterial berechnet und als Schätzung für \sigma^2 verwendet.