Moment

Moment

  • 5. Februar 2018
  • Posted by: Mika
Keine Kommentare

Momente sind Maßzahlen, die in der Mathematik für die Beschreibung einer Punktemenge verwendet werden. Hierdurch kannst Du die Verteilung einer Zufallsvariablen beschreiben.

Das Moment i-ter Ordnung m_i einer Zufallsvariablen X ist durch den Erwartungswert ihrer i-ten Potenz definiert:

    \begin{equation*} m_i = E(X^i) \end{equation*}

Die ersten theoretischen Momente von X sind also durch

    \begin{equation*} m_1= E(X), \quad m_2= E(X^2) \quad und \quad m_3= E(X^3) \end{equation*}

gegeben.

Setzt Du dagegen an die Stelle der Zufallsvariablen X ihre Differenz vom Mittelwert, (X-\mu), so sprichst Du von zentralen Momenten m^*_i:

    \begin{equation*} m^*_i = E[(X-\mu)^i] \end{equation*}

Die Verteilungsfunktion F(x) einer Zufallsvariablen X gibt die Wahrscheinlichkeit an, mit der die Zufallsvariable einen Wert kleiner oder gleich x annimmt; sie kann für verschiedene Zufallsvariablen folglich sehr unterschiedlich aussehen. Die Grafik zeigt einerseits (links) exemplarisch die Verteilungsfunktion einer diskreten Zufallsvariablen, die Du durch Kumulieren der Wahrscheinlichkeitsfunktion erhältst, und andererseits (rechts) die einer stetigen Zufallsvariablen mit linkssteiler Dichtefunktion, die sich als Integral über die Dichtefunktion ergibt:

Moment

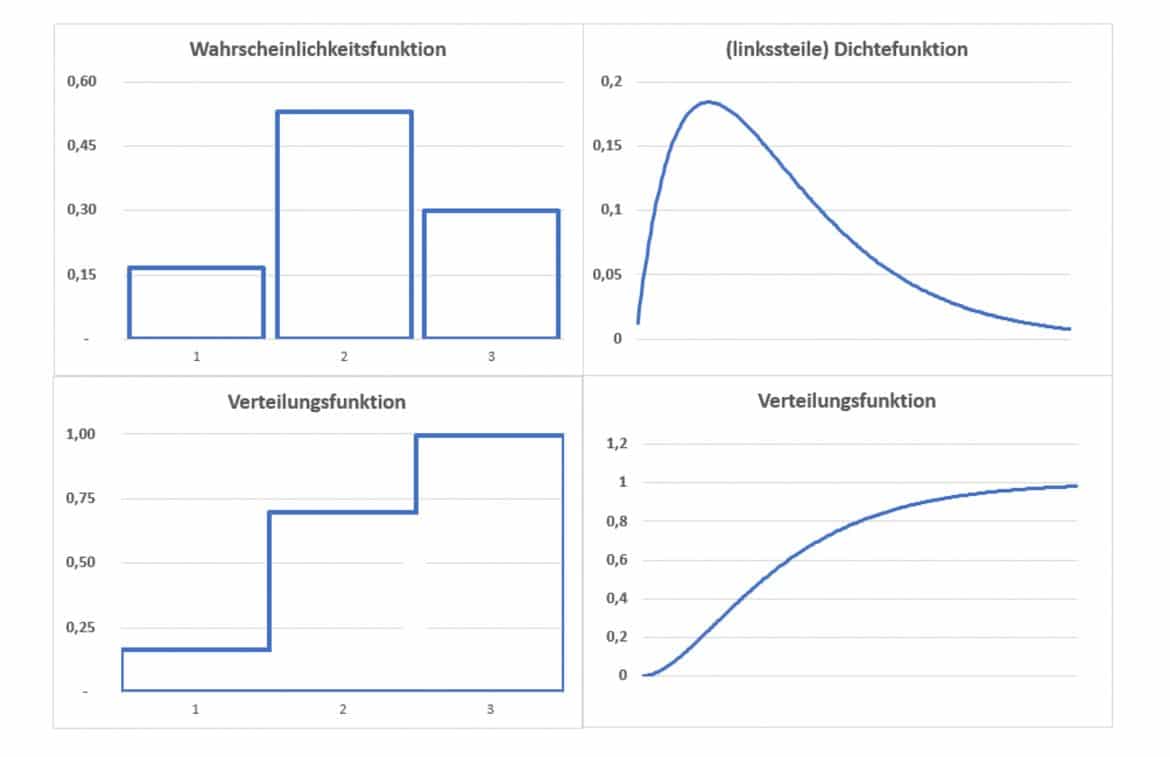
Charakterisierungen durch stochastische Maßzahlen

  • Erwartungswert, der die „Mitte“ der Verteilung angibt, den Wert, den die Zufallsvariable durchschnittlich also annimmt;
  • Varianz als Maß für die Streuung, ist die mittlere quadratische Abweichung der Realisationen vom Erwartungswert
  • Schiefe, die angibt, wie weit die Verteilung von einer symmetrischen Verteilung abweicht
  • Wölbung, ein Maß für die Spitzheit oder Flachheit einer Verteilung beziehungsweise ein Maß für die Abweichung von der Normalverteilung

Sie lassen sich durch die Momente bzw. zentralen Momente sehr einfach darstellen:

Den Erwartungswert kannst Du wie oben durch das Moment erster Ordnung darstellen.

Die Varianz wird durch das zentrale Moment 2. Ordnung gegeben:

    \begin{equation*} Var(X) = E([X-E(X)]^2) = m^*_2 \end{equation*}

Schiefe V und Wölbung W, auch höhere Momente genannt, lassen sich schließlich durch die zentralen Momente 3. und 4. Ordnung formulieren:

    \begin{equation*} V(X) = E([X-E(X)]^3) = m^*_3 \quad und \quad W(X) = E([X-E(X)]^4) = m^*_4 \end{equation*}

Falls die Momente von X existieren, könntest Du die Verteilungsfunktion aus ihnen bestimmen. Dieses Vorgehen nennt man Lösung des Momentenproblems.