Kovarianz

Kovarianz

  • 5. Februar 2018
  • Posted by: Mika
Keine Kommentare

Die Kovarianz ist ein Maß für den linearen Zusammenhang zwischen zwei Zufallsvariablen X und Y. Du erhältst sie als Erwartungswert des Produktes der Abweichungen beider Zufallsvariablen von ihrem Erwartungswert:

    \begin{equation*} Cov(X,Y) = E[(X-E(X))\cdot (Y - E(Y))] \end{equation*}

Das Vorzeichen der Kovarianz gibt Dir die Richtung des Zusammenhangs an: ist sie positiv, so besteht ein positiver linearer Zusammenhang zwischen X und Y, ist sie dagegen negativ, so tendieren hohe Werte von Y zu niedrigen Werten von X. Die absoluten Werte der Kovarianz von Paaren von Zufallsvariablen sind nicht vergleichbar, da die Kovarianz eine nicht standardisierte Maßzahl ist. Ein Wert von Null zeigt jedoch stochastische Unabhängigkeit an.

Berechnung für diskrete Zufallsvariablen

Für diskrete Zufallsvariablen X und Y mit den jeweils n möglichen Ausprägungen x_1,..x_n und y_1,…y_n, die mit den Wahrscheinlichkeiten p_1,…,p_n auftreten, kannst Du sie aus folgender Formel berechnen:

    \begin{equation*} Cov(X,Y) = \sum_{i=1}^n \sum_{j=1}^m p_{ij} \cdot (x_i-\mu_X) \cdot (y_j - \mu_Y), \quad mit \nobreakspace \mu_X=E(X) \nobreakspace und \nobreakspace \mu_Y=E(Y) \end{equation*}

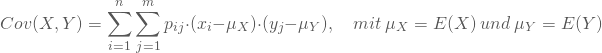
Bei einem Gewinnspiel liegen in einer Kiste beispielsweise 30 Kugelschreiber der Marken Taube und Park jeweils in den Farben rot, blau und schwarz. Du ziehst ohne in die Kiste zu schauen, einen Stift und erhältst je nach Marke und Farbe zudem die Auszahlungen X für die Marke (x_1=3 für Taube und x_2=5 für Park) sowie Y für die Farbe (y_1=-2 für rot, y_2=1 für blau und y_3=5 für schwarz).

Dich interessiert dann, ob zwischen X und Y ein Zusammenhang besteht. Die Wahrscheinlichkeiten p_{ij}=P(X=x_j;Y=y_j) der Tabelle sind als Laplace-Wahrscheinlichkeiten durch die Quotienten aus Anzahl der in Kombination (x_i;y_j) vorliegenden Stifte und der Gesamtzahl 30 extern gegeben.

p_{ij}=P(X=x_i;Y=y_j) Y
rot blau schwarz alle Farben
Auszahlung y_1=-2 y_2=1 y_2=5 p_{icdot{
X Taube x_1=3 0,07 0,17 0,10 0,33
Park x_2=5 0,10 0,23 0,33 0,67
beide Marken p_{cdotj} 0,17 0,40 0,43 1,00

Berechnung der Erwartungswerte

Zuerst berechnest Du die beiden Erwartungswerte durch Summierung der Produkte der Auszahlungsbeträge und ihrer Eintrittswahrscheinlichkeiten zu

    \begin{equation*} \mu_X = E(X) = \sum_{i=1}^2 x_i \cdot p_{i\cdot} = 3 \cdot 0,33 + 5 *0,67 = 4,3333 \end{equation*}

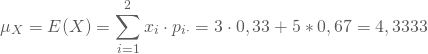
und

    \begin{equation*} \mu_Y = E(Y) = \sum_{j=1}^3 y_j \cdot p_{\cdot^j} = (-2) \cdot 0,17 + 1 \cdot 0,4 +5 \cdot 0,43 =2,2333 \end{equation*}

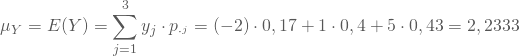
Setzt Du diese Werte dann in die Formel ein, so erhältst Du:

    \begin{equation*} Cov(X,Y) = \sum_{i=1}^n \sum_{j=1}^m p_{ij} \cdot (x_i-\mu_X) \cdot (y_j - \mu_Y) =0,07 \cdot (3-4,333)\cdot ((-2)-2,233) + ...+ 0,33 \cdot (5-4,333) \cdot (5-2,233) = 0,42 \end{equation*}

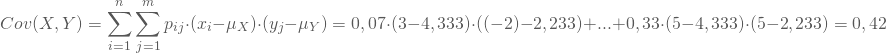
Mit Cov(X,Y)> 0 besteht also ein positiver Zusammenhang zwischen den Auszahlungsbeträgen für die Marke und denen für die Farbe. Aussagen über die Höhe der Kovarianz kannst Du dagegen nicht treffen, da sie eine nicht standardisierte Größe ist und sehr stark von der Skalierung abhängt.

Berechnung für stetige Zufallsvariablen

Im Fall von stetigen Zufallsvariablen X und Y und der gemeinsamen Dichtefunktion f(x,y) ist Deine Formel:

    \begin{equation*} Cov(X,Y) = \int_{-\infty}^{\infty} \nobreakspace \int_{-\infty}^{\infty} \nobreakspace f(x,y) \cdot (x-\mu_X) \cdot (y - \mu_Y)\nobreakspace dx, \end{equation*}

Wenn X und Y Zufallsvariablen und a, b, c, d Konstante sind, lauten Deine Rechenregeln für die Kovarianz:
Die Kovarianz ist symmetrisch, d.h. die Kovarianz von X und Y ist gleich der von Y und X:

    \begin{equation*} Cov(X ,Y ) = Cov(Y,X) \end{equation*}

Die Kovarianz zwischen einer Zufallsvariablen X und der mit (-1) multiplizierten Zufallsvariablen Y ist gleich dem negativen Wert der Kovarianz von X und Y:

    \begin{equation*} Cov(X , -Y ) = -Cov(X,Y) \end{equation*}

Die Kovarianz von Linearkombinationen Deiner Zufallsvariablen ist gleich dem Produkt aus Koeffizienten und der Kovarianz der Zufallsvariablen:

    \begin{equation*} Cov(a\cdot X + b ; c\cdot Y +d) = a\cdot c\cdot Cov(X,Y) \end{equation*}

Du kannst die Kovarianz analog zum Verschiebungssatz bei der Varianz als Funktion von Erwartungswerten schreiben:

    \begin{equation*} Cov(X,Y) = E(X \cdot Y) - E(X) \cdot E(Y) \end{equation*}

Anstelle der Kovarianz wird häufig der Korrelationskoeffizient nach Bravais-Pearson als Maß für den linearen Zusammenhang zwischen zwei metrischen Zufallsvariablen verwendet, der als Quotient aus Kovarianz und der Wurzel aus dem Produkt beider Varianzen maßstabsunabhängig ist:

    \begin{equation*} \rho = \frac {Cov(X,Y)} {\sqrt{Var(X) \cdot Var(Y)} } \end{equation*}

Du kannst den Korrelationskoeffizienten als standardisierte Kovarianz interpretieren; da er immer im Intervall [0;1] liegt, zeigt er nicht nur die Richtung des Zusammenhangs an, sondern dient auch als Maß für dessen Stärke.