Erwartungswert

Erwartungswert

  • 5. Februar 2018
  • Posted by: Mika
Keine Kommentare

Führst Du ein Zufallsexperiment durch, so kannst Du den Ausgang dieses Experiments als Realisation einer Zufallsvariablen X ansehen mit einem bestimmten Erwartungswert. Genauer gesagt folgt X einer Verteilung, die Du durch ihre Verteilungsparameter beschreiben kannst.

Als Erwartungswert \mu = E(X) von X bezeichnet man den Wert, den X im Mittel annimmt.

Stell Dir beispielsweise vor, Du wirfst eine symmetrische Münze. Mit jedem Wurf kann Deine Zufallsvariable entweder den Wert 0 annehmen, wenn „Kopf“ fällt, oder 1, wenn „Zahl“ realisiert wird. Die Wahrscheinlichkeit beträgt im Fall einer symmetrischen Münze für beide Ausgänge 50\%. Dann nimmt die Zufallsvariable im Mittel den Wert

    \begin{equation*} 0,5 \cdot 0 + 0,5 \cdot 1 = 0,5 \end{equation*}

an.

Erwartungswert einer diskreten Zufallsvariablen

Bezeichnest Du allgemein x_i als diskrete mögliche Realisationen Deiner Zufallsvariablen, mit i = 1,…n, und p_i = P(X=x_i) als die theoretischen Wahrscheinlichkeiten für das Eintreten der x_i, so erhältst Du den Erwartungswert als

    \begin{equation*} \mu = E(X) = \sum_{i=1}^n x_i \cdot p_i \end{equation*}

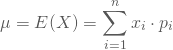
Bei einem Spiel gibt es drei mögliche Ausgänge x_1,x_2,x_3, die mit den Wahrscheinlichkeiten p_1,p_2,p_3 eintreten:

Situation Auszahlungsbetrag Wahrscheinlichkeit
1 Du allein gewinnst 1500 € x_1=1500 p_1=0,1
2 Du gehst leer aus x_2=0 p_1=0,7
3 Du verlierst und musst 1000 € zahlen x31=-1000 p_3=0,2

 

Du überlegst, bei diesem Spiel mitzuspielen; vorher möchtest Du aber den Erwartungswert des Auszahlungsbetrags berechnen, um zu wissen, welchen Betrag Du im Mittel erhältst:

    \begin{equation*} \mu = E(X) = \sum_{i=1}^3 x_i \cdot p_i = 1500 \cdot 0,1 + 0 \cdot 0,7 + (-1000) \cdot 0,2 = -50 \end{equation*}

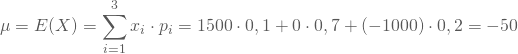
Da das Spiel einen negativen Erwartungswert hat, solltest Du vom Spielen absehen.

Erwartungswert einer stetigen Zufallsvariablen

Ist X eine stetige Zufallsvariable, so ist die Wahrscheinlichkeit für das Auftreten eines bestimmten Wertes Null. Bei der Definition des Erwartungswertes tritt an die Stelle der Wahrscheinlichkeiten der Wert der Dichtefunktion f(x) und Du integrierst anstelle zu summieren:

    \begin{equation*} \mu = E(X) = \int_{-\infty}^{\infty} \quad x \cdot f(x) dx \end{equation*}

Hast Du zwei Zufallsvariablen X und Y gegeben, so wird der Erwartungswert aus beiden wie folgt gebildet:

    \begin{equation*} E(a\cdot X + b \cdot Y) = a \cdot E(X) + b \cdot E(Y) \end{equation*}

bzw. als dessen Spezialfall:

    \begin{equation*} E(a\cdot X + b) = a \cdot E(X) + b \end{equation*}

Der Erwartungswert ist also linear.