Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Mehrdimensionale Normalverteilung
- 25. April 2018
- Posted by: Mika
Die eindimensionale Normalverteilung hast Du durch die Dichtefunktion
![]()
mit den beiden Parametern ![]() und
und ![]() gegeben.
gegeben.
Betrachtest Du eine mehrdimensionale normalverteilte Zufallsvariable ![]() , so musst Du als Parameter der gemeinsamen Verteilung neben dem Mittelwertvektor
, so musst Du als Parameter der gemeinsamen Verteilung neben dem Mittelwertvektor ![]() und den Varianzen
und den Varianzen ![]() auch die Kovarianzen
auch die Kovarianzen ![]() als Maß für die Abhängigkeit zwischen je zwei Variablen berücksichtigen.
als Maß für die Abhängigkeit zwischen je zwei Variablen berücksichtigen.
Ist ![]() Deine Kovarianzmatrix und
Deine Kovarianzmatrix und ![]() Dein n-dimensionaler Mittelwertvektor
Dein n-dimensionaler Mittelwertvektor
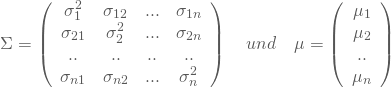
,
und ist ![]() , so lautet die mehrdimensionale Normalverteilung:
, so lautet die mehrdimensionale Normalverteilung:
![]()
Die erste Grafik zeigt die Dichtefunktionen einer bivariaten standardisierten Normalverteilungen von zwei unabhängigen Einzelvariablen, bei denen die Kovarianz zwischen ![]() und
und ![]() also Null beträgt:
also Null beträgt:
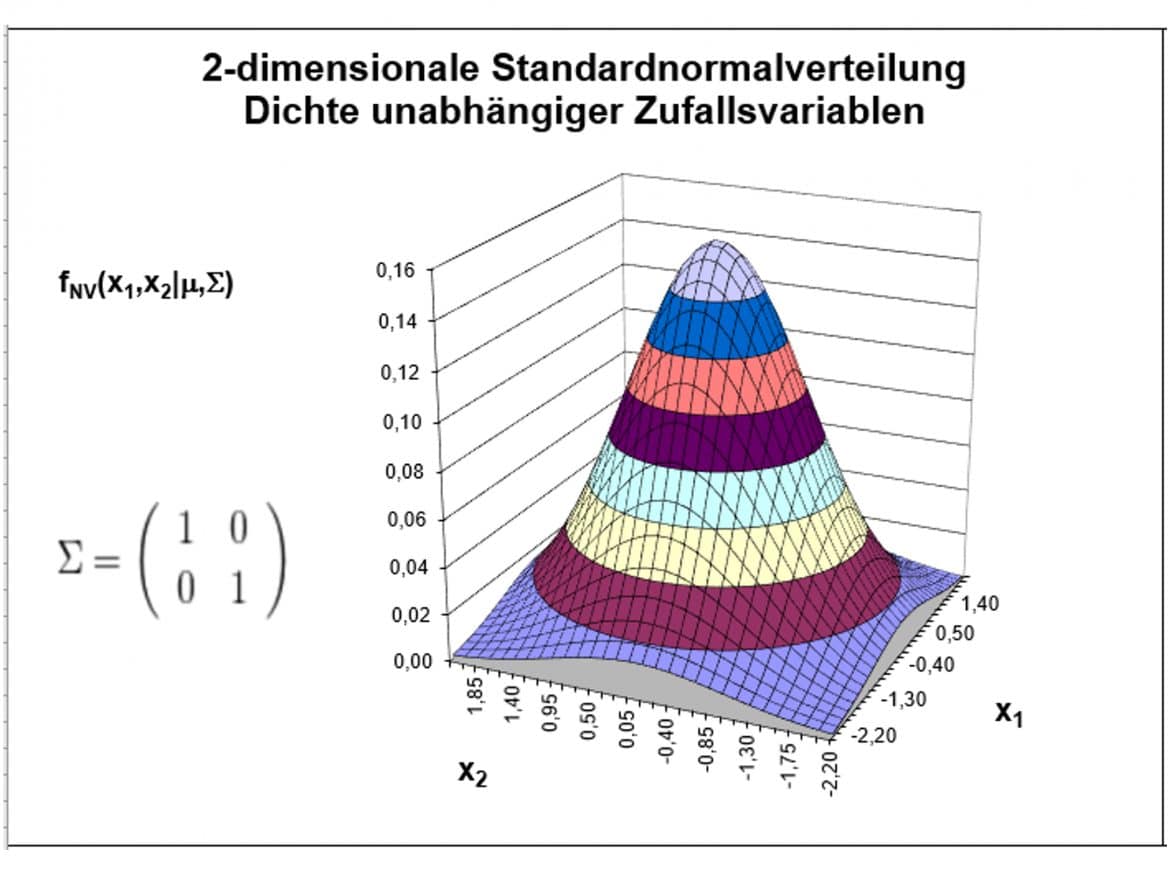
Die Dichte der Funktion nimmt den höchsten Wert an der Stelle ![]() ein; von da aus nimmt sie in alle Richtungen gleichmäßig ab.
ein; von da aus nimmt sie in alle Richtungen gleichmäßig ab.
Untersuchst Du etwa die zweidimensionale Zufallsvariable X=(Körpergröße; Gewicht) von Männern, so vermutest Du zwischen beiden Variablen keine Abhängigkeit und die gemeinsame Dichtefunktion sollte aussehen wie die der ersten Grafik.
Die zweite Grafik zeigt die Dichtefunktion von zwei positiv abhängigen Zufallsvariablen mit einer Kovarianz von ![]() . Die Varianz-Kovarianz-Matrix lautet demnach
. Die Varianz-Kovarianz-Matrix lautet demnach
![]()
Du kannst in der zweiten Grafik die Abhängigkeit der Zufallsvariablen deutlich am Übergang von der „runden“ zur „ovalen“ Dichtefunktion erkennen: große Abweichungen der Zufallsvariablen ![]() von Ihrem Mittelwert sind häufiger mit ebenfalls größeren gleichgerichteten Abweichungen von
von Ihrem Mittelwert sind häufiger mit ebenfalls größeren gleichgerichteten Abweichungen von ![]() von dem Mittelwert
von dem Mittelwert ![]() verbunden.
verbunden.
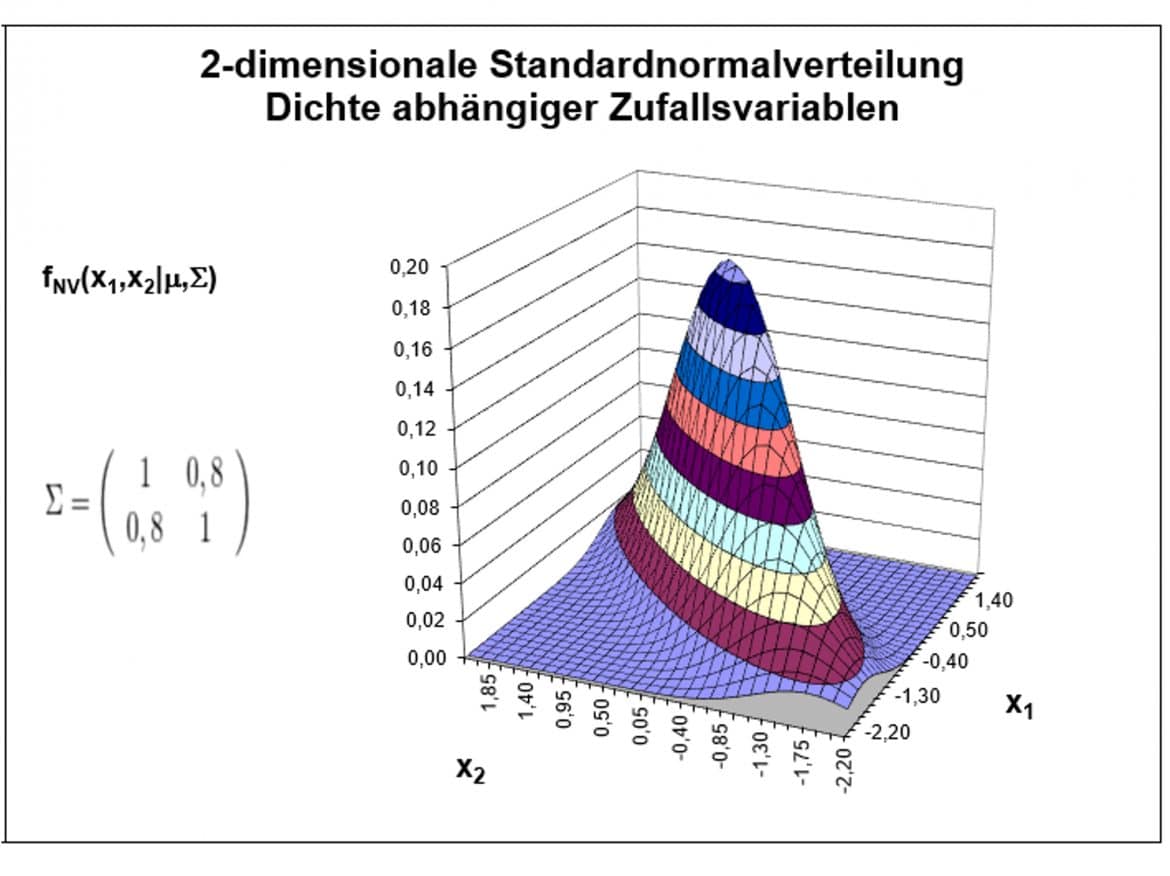
Betrachtest Du beispielsweise die zweidimensionale Zufallsvariable Y=(Körpergröße; Gewicht), so sind extrem große Menschen meistens auch deutlich schwerer als der Durchschnitt und umgekehrt.
Die mehrdimensionale Normalverteilung ist die Grundlage vieler statistischer Modelle.
