Marginalverteilung / Randverteilung

Marginalverteilung / Randverteilung

  • 25. April 2018
  • Posted by: Mika
Keine Kommentare

Deine mehrdimensionale Zufallsvariable X=(X_1,..,X_n) lässt sich durch eine gemeinsame Verteilung der X_i beschreiben. Als Marginal- oder Randverteilung bezeichnest Du die Verteilung einer Einzelvariablen, wenn die Realisationen der anderen Variablen nicht berücksichtigt werden.

Dabei kannst Du wieder den diskreten vom stetigen Fall unterscheiden:

Diskreter Fall:

Du hast beispielsweise die zweidimensionale Wahrscheinlichkeitsfunktion p_{ij} = P(X_1=i;X_2=j) für Deutschnoten X_1 von Jungen und Mädchen X_2 wie folgt bestimmt:

p_{ij} X_2: Geschlecht
1: Mädchen 2: Jungen Summe
X_1: Deutschnote 1 0,061 0,030 0,091
2 0,273 0,152 0,424
3 0,182 0,212 0,394
4 0,030 0,061 0,091
Summe 0,545 0,455 1

Im Inneren der Tabelle stehen die p_{ij}, mit denen ein willkürlich gewählter Schüler die Deutschnote i und das Geschlecht j besitzt: so ist p_{32}=0,212 die Wahrscheinlichkeit mit der ein willkürlich ausgewählter Schüler die Deutschnote 3 erzielt hat und männlich ist.

Die Zeilensummen geben dann die Wahrscheinlichkeiten p_{i \cdot} an, mit der ein willkürlich ausgewählter Schüler die jeweilige Deutschnote erzielt: Das ist die Rand- oder Marginalverteilung von X_1.

    \begin{equation*} p_{i \cdot}= \displaystyle\sum_{j=1}^2 p_{ij} \quad und \quad p_{\cdot j}= \displaystyle\sum_{i=1}^3 p_{ij} \end{equation*}

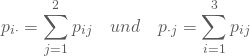
Die Randverteilung p_{\cdot j} von X_2, also die Spaltensummen, geben Dir an, mit welcher Wahrscheinlichkeit ein willkürlich herausgegriffener Schüler weiblich oder männlich ist.

Betrachtest Du anstelle der Wahrscheinlichkeitsfunktion die Verteilungsfunktion F_{ij} = P(X_1\le i;X_2 \le j), so erhältst Du als Randverteilung F_{i \cdot} die Wahrscheinlichkeit, mit der ein Schüler mindestens die Note i erzielt.

Stetiger Fall:

Im stetigen Fall hast Du etwa für zwei Zufallsvariablen X und Y eine gemeinsame Dichtefunktion f(X,Y) gegeben.

Du erhältst daraus die Dichtefunktion für X ohne Berücksichtigung der Realisationen von Y, indem Du über alle möglichen Realisationen von Y integrierst:

    \begin{equation*} f(X)= \int_{-\infty}^{\infty} \nobreakspace f(X,Y) \nobreakspace dy \end{equation*}

und die für Y, indem Du über den Definitionsbereich von X integrierst:

    \begin{equation*} f(Y)= \int_{-\infty}^{\infty} \nobreakspace f(X,Y) \nobreakspace dx \end{equation*}

Betrachtest Du nicht die Dichte- sondern die Verteilungsfunktion F(X,Y), so erhältst Du daraus analog die Randverteilung von Y ohne Berücksichtigung von X als Wahrscheinlichkeit, mit der Y kleiner oder gleich y ist.

    \begin{equation*} F(Y)= \int_{-\infty}^{\infty} \nobreakspace F(X,Y) \nobreakspace dx \end{equation*}

Im Falle einer mehr als zweidimensionalen Verteilung erhältst du die Randverteilungen der k-ten Einzelvariablen, indem Du über alle anderen Variablen integrierst.