Gemeinsame Verteilung

Gemeinsame Verteilung

  • 25. April 2018
  • Posted by: Mika
Keine Kommentare

Voneinander abhängige Zufallsvariablen X_1,…,X_n solltest Du als eine mehrdimensionale Zufallsvariable X=(X_1,..,X_n) betrachten und durch eine gemeinsame Verteilung beschreiben.

Dabei unterscheidest Du zwischen diskreten und stetigen Zufallsvariablen.

Diskreter Fall:

Eine Untersuchung im Auftrag des Schulamts hat eine gemeinsame Verteilung der zweidimensionalen Zufallsvariablen aus Körpergröße und Gewicht bei Schülern der ersten Klasse ermittelt, wobei beide Zufallsvariablen in Intervallen gruppiert erhoben wurden:

Die erste Tabelle zeigt die zweidimensionale Wahrscheinlichkeitsfunktion:

Gewicht in kg bis 18 kg über 18 bis 24 kg über 24 kg Summe
Körpergröße p_{ij} j=1 j=2 j=3
bis 120 cm i=1 10,64% 4,26% 2,13% 17,02%
über 120 cm bis 125 cm i=2 6,38% 36,17% 6,38% 48,94%
über 125 cm i=3 2,13% 25,53% 6,38% 34,04%
Summe 19,15% 65,96% 14,89% 100,00%

Demnach beträgt die Wahrscheinlichkeit p_{22}, dass ein willkürlich herausgegriffener Erstklässler zwischen 120cm und 125 cm groß ist und zwischen 18 und 24 kg wiegt, gerade 36,17\%.

Diskrete gemeinsame Wahrscheinlichkeitsfunktion

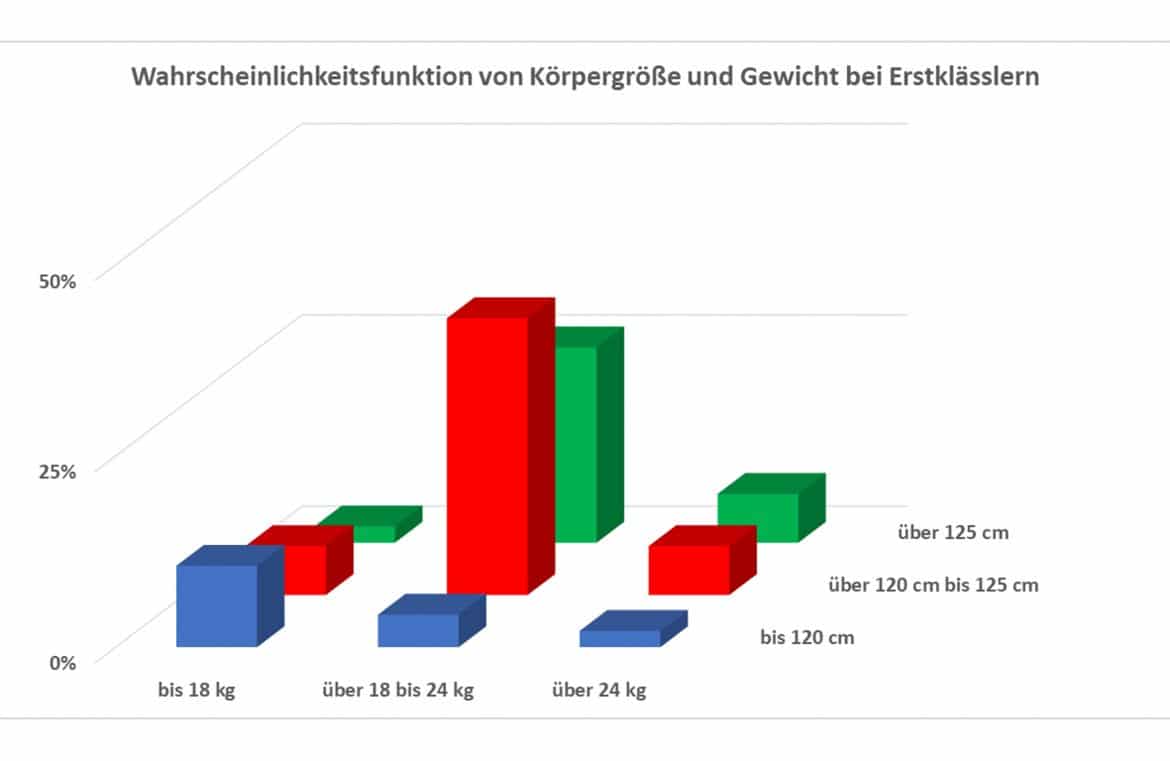
Durch Kumulieren der Wahrscheinlichkeitsfunktion erhältst Du die Verteilungsfunktion F: So erhältst Du F_{22} als Summe der Wahrscheinlichkeiten aller Merkmalskombinationen, für die gilt: i \le 2 und j \le 2, es ist also F_{22}=p_{11}+p_{21}+p_{12}+p_{22}.

Gewicht in kg
 bis 18 kg über 18 bis 24 kg über 24 kg
Körpergröße F_{ij} j=1 j=2 j=3
bis 120 cm i=1 10,64% 14,89% 17,02%
über 120 cm bis 125 cm i=2 17,02% 57,45% 65,96%
über 125 cm i=3 19,15% 85,11% 100,00%

Die Wahrscheinlichkeit F_{22}, mit der ein zufällig ausgewählter Schüler mindestens 120 bis 125 cm groß ist und mindestens in der Gewichtsklasse 18 – 24 kg liegt, beträgt 57,45\%.

Diskrete gemeinsame Verteilung

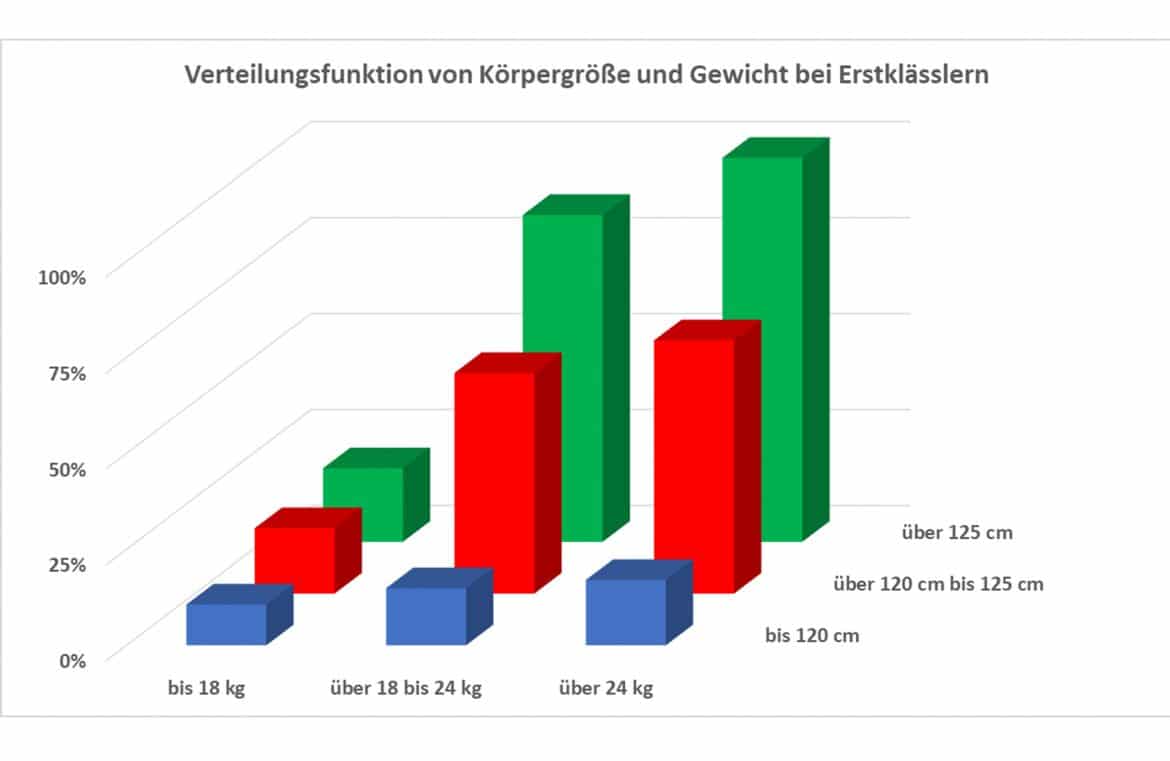
Stetiger Fall:

Hast Du stetige mehrdimensionale Zufallsvariablen (mit unendlich vielen möglichen Ausprägungen) vorliegen, so beträgt die Wahrscheinlichkeit, mit der eine bestimmte Wertekombination eintritt, immer Null. An die Stelle der mehrdimensionalen Wahrscheinlichkeitsfunktion im diskreten Fall tritt daher die mehrdimensionale Dichtefunktion, die angibt, wie dicht sich mögliche Realisationen von X=(X_1,..,X_n) um x=(x_1,…,x_n) scharen.

Die mehrdimensionale Verteilungsfunktion erhältst Du aus der Dichtefunktion durch Integrieren über alle Zufallsvariablen.

Du betrachtest etwa wieder die zweidimensionale Zufallsvariable X=(Körpergröße, Gewicht), gruppierst aber nicht, sondern betrachtest dieses Mal die stetigen Zufallsvariablen. Aus langjährigen Beobachtungen kennst Du ihre Dichtefunktion als:

    \begin{equation*} f(x,y) = \begin{cases} 0 \quad f\"ur \nobreakspace x< 110\nobreakspace und \nobreakspace y < 10\\ \\ \frac {3x + y}{152000} \quad f\"ur \nobreakspace 110 \le x< 130\nobreakspace und \nobreakspace 10 \le y < 30\\ \\ 0, \quad sonst \end{equation*}

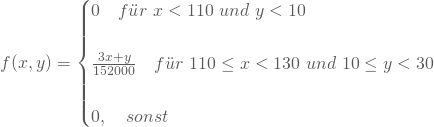
Daraus erhältst Du die mehrdimensionale Verteilungsfunktion, indem Du nacheinander über x und über y integrierst:

    \begin{equation*} F(x,y) = \begin{cases} 0 \quad f\"ur \nobreakspace x< 110\nobreakspace und \nobreakspace y < 10\\ \\ \displaystyle\int_{110}^{130} \int_{10}^{30} f(x,y) dx \nobreakspace dy \\ \\ 1, \quad sonst \end{equation*}

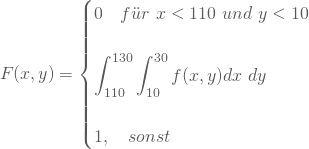
Bildest Du im mittleren Definitionsbereich die Integrale über x und über y, und setzt für beide Variablen die Randwerte ein, so erhältst Du

    \begin{equation*} F(x,y) = \left[ \left[ \frac {3 x^2y +xy^2}{304000}\right]_{110}^{130}\right]_{10}^{30} = 1 \end{equation*}

Stetige Verteilung

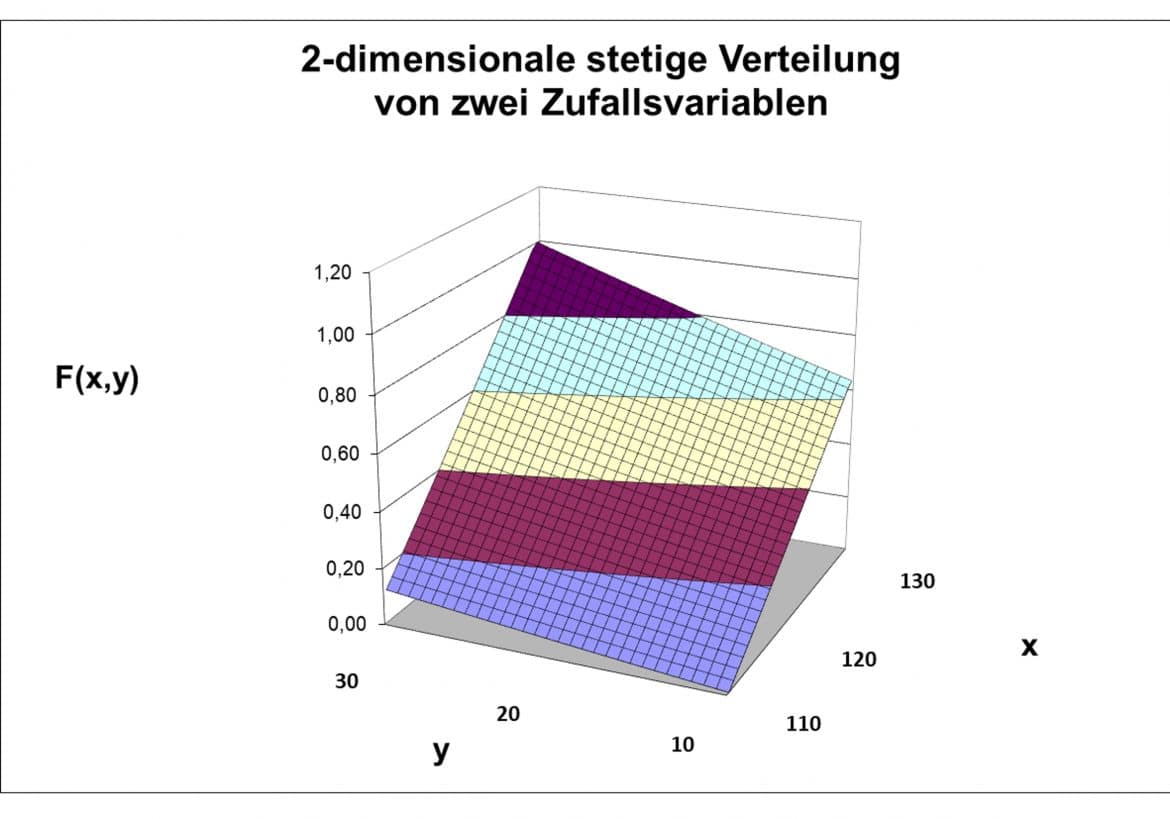
Die Grafik zeigt diese stetige Verteilungsfunktion.

Für viele statistische Anwendungen benötigst Du vor allem die mehrdimensionale Normalverteilung, die vielen empirischen Phänomen gerecht wird. Für große Stichproben lassen sich andere Verteilungen durch sie approximieren.