Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Gesetz der großen Zahlen
- 5. Februar 2018
- Posted by: Mika
Ein Zufallsexperiment kann zu verschiedenen Ausgängen führen, zu denen jeweils feste aber in der Regel unbekannte theoretische Wahrscheinlichkeiten gehören. Führst Du das Experiment mehrmals hintereinander aus, so erhältst Du relative Häufigkeiten, mit denen die verschiedenen Ausgänge auftreten.
Das Gesetz der großen Zahlen besagt nun, dass Deine beobachteten relativen Häufigkeiten ![]() sich mit zunehmender Anzahl n ausgeführter Experimente immer mehr an die theoretischen Wahrscheinlichkeiten
sich mit zunehmender Anzahl n ausgeführter Experimente immer mehr an die theoretischen Wahrscheinlichkeiten ![]() annähern. Dann konvergiert die durchschnittliche mittlere Abweichung zwischen den Zufallsvariablen
annähern. Dann konvergiert die durchschnittliche mittlere Abweichung zwischen den Zufallsvariablen ![]() und ihrem Erwartungswert
und ihrem Erwartungswert ![]() gegen Null.
gegen Null.
Wie kann man das Gesetz der großen Zahlen formal aufschreiben?
Der Erwartungswert einer Zufallsvariablen lässt sich als arithmetisches Mittel der möglichen Ereignisse, multipliziert mit deren Wahrscheinlichkeit darstellen:
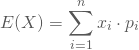
Führst Du Dein Zufallsexperiment beispielsweise m mal durch und bezeichnest ![]() als j-te Realisationen, so kannst Du die mittlere Abweichung zwischen den Realisationen von X und ihrem Mittelwert schreiben als:
als j-te Realisationen, so kannst Du die mittlere Abweichung zwischen den Realisationen von X und ihrem Mittelwert schreiben als:
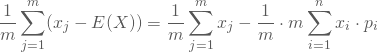
Setzt Du dann ![]() als Anzahl, mit der Du die i-te Realisation von X beobachtest hast, und
als Anzahl, mit der Du die i-te Realisation von X beobachtest hast, und ![]() als relative Häufigkeit von
als relative Häufigkeit von ![]() , so erhältst Du
, so erhältst Du
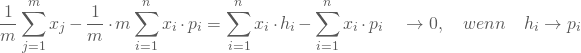
Nach dem Gesetz der großen Zahlen konvergieren die relativen Häufigkeiten ![]() für große n gegen die Wahrscheinlichkeiten
für große n gegen die Wahrscheinlichkeiten ![]() ; dann konvergiert die linke Summe gegen die rechte und ihre Differenz gegen Null.
; dann konvergiert die linke Summe gegen die rechte und ihre Differenz gegen Null.
Praktisches Beispiel
Das kannst Du mit einem symmetrischen Würfel ganz einfach ausprobieren. Jede Augenzahl von eins bis sechs besitzt die theoretische Wahrscheinlichkeit ![]() . Du wirfst jetzt den Würfel und notierst bei jedem Wurf seine Augenzahl und erhältst zum Beispiel die folgenden Zahlen:
. Du wirfst jetzt den Würfel und notierst bei jedem Wurf seine Augenzahl und erhältst zum Beispiel die folgenden Zahlen:
| Würfe 1 bis 10 | Würfe 11 bis 20 | Würfe 1 bis 30 | |||||||||||||||||||||||||||||
| 3 | 6 | 3 | 3 | 3 | 5 | 6 | 6 | 6 | 6 | 2 | 6 | 5 | 6 | 6 | 4 | 4 | 2 | 1 | 3 | 4 | 5 | 6 | 2 | 3 | 5 | 1 | 4 | 1 | 2 | ||
Bestimmung von Häufigkeiten
Dann kannst Du die absoluten und relativen Häufigkeiten bestimmen, mit denen jede Augenzahl nach 10, 20, 30 oder auch 100 Würfen aufgetreten ist. Du erhältst zum Beispiel:
| 10 Würfe |
20 Würfe |
30 Würfe |
|||||||||||
| Augenzahl | absolute Häufigkeit | relative Häufigkeit | Augenzahl | absolute Häufigkeit | relative Häufigkeit | Augenzahl | absolute Häufigkeit | relative Häufigkeit | |||||
| 1 | 1 | 0,100 | 1 | 3 | 0,150 | 1 | 4 | 0,133 | |||||
| 2 | 4 | 0,400 | 2 | 6 | 0,300 | 2 | 7 | 0,233 | |||||
| 3 | 2 | 0,200 | 3 | 2 | 0,100 | 3 | 4 | 0,133 | |||||
| 4 | 1 | 0,100 | 4 | 3 | 0,150 | 4 | 6 | 0,200 | |||||
| 5 | 1 | 0,100 | 5 | 3 | 0,150 | 5 | 4 | 0,133 | |||||
| 6 | 1 | 0,100 | 6 | 3 | 0,150 | 6 | 5 | 0,167 | |||||
| 10 | 1,000 | 20 | 1,000 | 30 | 1,000 | ||||||||
| mittlere Abweichung | |||||||||||||
Nach zehn Würfen ist in diesem Beispiel die Augensumme 2 viermal aufgetreten, die drei zweimal und alle anderen Augensummen je einmal. Die relativen Häufigkeiten weichen bei den wenigen beobachteten Würfen stark von den theoretischen Wahrscheinlichkeit ![]() ab. Die mittlere Abweichung als Mittelwert der absoluten Abweichungen zwischen relativen Häufigkeiten und theoretischen Wahrscheinlichkeiten ist ein Maß hierfür.
ab. Die mittlere Abweichung als Mittelwert der absoluten Abweichungen zwischen relativen Häufigkeiten und theoretischen Wahrscheinlichkeiten ist ein Maß hierfür.
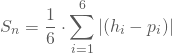
Nach 10 Würfen erhältst Du also:
![]()
![]() beträgt 0,0889. Nach 20 bzw. 30 Würfen nähern sich die relativen Häufigkeiten langsam an die theoretischen Wahrscheinlichkeiten an und Deine mittlere Abweichungen
beträgt 0,0889. Nach 20 bzw. 30 Würfen nähern sich die relativen Häufigkeiten langsam an die theoretischen Wahrscheinlichkeiten an und Deine mittlere Abweichungen ![]() und
und ![]() sinken folglich im Beispiel.
sinken folglich im Beispiel.
Anschauliche Interpretation
Diese Gesetzmäßigkeit lässt sich anschaulich dadurch erklären, dass der Einfluss von Ausreißern mit zunehmendem Umfang des Experiments abnimmt.
Das Gesetz der großen Zahlen findest Du in zwei Versionen: Im Falle der schwachen Formulierung konvergiert die Wahrscheinlichkeit, mit der die mittlere Abweichung ![]() größer als ein beliebiges
größer als ein beliebiges ![]() ist, für unendliche n gegen Null; nach der starken Formulierung konvergiert
ist, für unendliche n gegen Null; nach der starken Formulierung konvergiert ![]() dagegen fast sicher gegen Null.
dagegen fast sicher gegen Null.
Das Gesetz der großen Zahlen ist übrigens für viele praktische Anwendungen von großer Bedeutung. Der verfälschende Einfluss von Messfehlern und Zufall kann durch dieses Gesetz bei ausreichend großem Erhebungsumfang minimiert werden. Was als ausreichend großer Stichprobenumfang gilt, ist allerdings nicht eindeutig bestimmt; vorsichtige Statistiker wenden den Satz bei n>100 an, in vielen Untersuchungen unterstellt man ihn schon für n>30.
Versicherungen zum Beispiel können Schadenshäufigkeiten umso präziser vorhersagen und ihre Kosten danach kalkulieren, je größer die Anzahl der versicherten Personen, Häuser, Gefahrengüter etc. mit gleicher Schadenswahrscheinlichkeit ist.
