Konvergenzaussagen in der Wahrscheinlichkeitstheorie

Was bedeuten Konvergenzaussagen in der Wahrscheinlichkeitstheorie? Hier geht es darum zu verstehen, was passiert wenn man immer mehr Daten sammelt – also theoretisch unendlich viele.

Mathematisch heißt das konkret: Wiederholst Du ein Zufallsexperiment beispielsweise n-mal, so kannst Du seine Ausgänge als Realisationen von n Zufallsvariablen betrachten, die unabhängig und identisch verteilt sind. Jede dieser Zufallsvariablen kann sich zudem in verschiedenen Ereignissen realisieren. Diesen entspreschen (meist unbekannte) aber für alle i gleiche theoretische Häufigkeiten.

Welche wichtigen Konvergenzaussagen gibt es?

Die Konvergenzaussagen der Wahrscheinlichkeitstheorie liefern Dir im Grunde genommen Aussagen, die für große Stichprobengrößen näherungsweise erfüllt sind. Was in diesem Fall groß bedeutet ist natürlich eine wichtige Frage. In vorsichtiger Formulierung sollte die Stichprobengröße n mindestens 100 sein.

• Nach dem Gesetz der großen Zahlen nähern sich die relativen Häufigkeiten, mit denen die verschiedenen Ereignisse auftreten, asymptotisch an deren theoretische Wahrscheinlichkeiten an.
• Gemäß dem Zentralen Grenzwertsatz nähern sich Summe und Mittelwert der 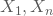mit zunehmendem n an die Normalverteilung an, unabhängig davon, welcher Verteilung die 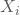folgen.

Beide Aussagen erlauben es Dir, induktive statistische Verfahren auf die Parameter der Zufallsvariablen anzuwenden, die aufgrund der unbekannten Verteilung der Zufallsvariablen selbst nicht anwendbar wären. In der Praxis ist das extrem hilfreich. Denn man erhält damit Voraussetzungen für bestimmte Verfahren bei genügend großer Datenbasis quasi gratis dazugeliefert.