Stichprobenumfang

Nachdem Du Dich entschieden hast, wie die Stichprobe zustande kommt, stellt sich noch die Frage nach einem geeigneten Stichprobenumfang.

Größere Stichproben bewirken kleinere Konfidenzintervalle, also eine präzisere Schätzung von Stichprobenkennwerten und eine höhere Power. Power oder auch Teststärke ist die Wahrscheinlichkeit, einen vorhandenen Effekt auch tatsächlich aufzudecken.

Das Verhältnis von Stichprobenumfang, Effektgröße und Teststärke wird hier einmal für den Fall von Mittelwertsunterschieden genauer beleuchtet. Angenommen Du untersuchst die einfache Fragestellung, ob sich die Mittelwerte von zwei Gruppen signifikant unterscheiden. Dich interessiert, was die optimale Stichprobengröße für diese Untersuchung ist.

Angenommen die Nullhypothese H0 gilt in der Population, das bedeutet, der Mittelwertunterschied ist null in der Population. Die Wahrscheinlichkeiten für verschiedene Mittelwerte folgt einer -Verteilung mit dem Mittelwert Null. Je größer die Stichprobe, desto geringer ist die Wahrscheinlichkeit, große Abweichungen von der wahren Mittelwertdifferenz zu finden. Das heißt, je größer die Stichprobe, desto unwahrscheinlicher werden gefundene Mittelwertsunterschiede weit entfernt von der Null, also wird die Standardabweichung kleiner. Die Dichtefunktion für die gefundenen Mittelwertsunterschiede ist die der Normalverteilung mit dem Mittelwert 0 und der Standardabweichung

   

wobei die Standardabweichung des Merkmals in der Population ist.

Angenommen, in der Population gilt die Alternativhypothese H1 mit einer Effektstärke von , das heißt, der wahre Mittelwertsunterschied beträgt . Dann hat die Dichteverteilung für die H1 die gleiche Form wie die der H0, nur ist ihr Mittelwert bei und nicht bei Null. Der kritische -Wert liegt am rechten Rand der Verteilung unter der Nullhypothese, und zwar genau so, dass rechts vom -Wert die Fläche unter der Kurve 0.05 (also gleich dem Alpha-Fehler) ist. Die kritischen -Werte sind in den unten gezeichneten Graphen eingezeichnet.

Wenn sich die Kurven der beiden Verteilungen extrem stark überlappen, ist die Stichprobe zu klein, das heißt, Deine Untersuchung hat eine geringe Teststärke. Das bedeutet, dass die Wahrscheinlichkeit, einen Verpasser zu machen, auch Fehler zweiter Art genannt, sehr groß ist. Oder mit anderen Worten, es kann sein, dass der Test nicht signifikant wird, obwohl tatsächlich ein Mittelwertsunterschied vorliegt, die Untersuchung war bloß zu „schwach“, diesen Effekt zu finden. Der Betafehler lässt sich auch in der untenstehenden Grafik („StichprobenumfangzuKlein“) erkennen: Er ist die rot schraffierte Fläche, also all jene Bereiche unterhalb der H1-Verteilung, in denen die Nullhypothese beibehalten würde (also das Testergebnis nicht signifikant ist), obwohl die H1 gültig ist.

Es kann auch den umgekehrten Fall einer „zu großen“ Stichprobe geben. Das mag Dich vielleicht überraschen, denn überall hört man Forderungen nach möglichst großen Stichproben. Bei extrem großen Stichproben werden beinahe beliebig kleine Mittelwertsunterschiede signifikant. Dieser mag in Wirklichkeit minimal und völlig unbedeutend sein, aber dennoch suggeriert das „signifikante Testergebnis“ es liege ein Unterschied vor. Wenn diese Effekte publiziert und als signifikante Effekte kommuniziert werden, entsteht ein verzerrter Eindruck. Woran liegt das?

Nun, wenn man zweimal eine Stichprobe zieht, dann werden deren Mittelwerte in einem bestimmten Merkmal niemals identisch sein. Bleiben wir bei dem einfachen Beispiel der Körpergröße. Wenn Du zufällig 100 Personen aus Deiner Stadt auswählst und ihre Größe misst, wird sich das Ergebnis von einer anderen Stichprobe, die Deine Kommilitonin am Vortag erhoben hat, seien es nur um einige Millimeter, unterscheiden. Der Mittelwert in Deiner Stichprobe ist dann möglicherweise bei 173,2mm und in der Stichprobe Deiner Kommilitonin etwa 174,5mm.

Und das, obwohl ihr zweimal Probanden aus derselben Population rekrutiert habt. Dieser Unterschied liegt normalerweise im Bereich erwarteter Zufallsschwankungen und ein -Test würde dessen Nicht-Signifikanz bescheinigen. In die Berechnung des Standardfehlers fließt die Stichprobengröße in den Nenner ein. Das heißt, je größer die Stichprobe, desto kleiner der Standardfehler. Der Standardfehler wiederum geht in die Berechnung der -Prüfstatistik im Nenner ein. Kleinere Standardfehler bewirken also größere empirische -Werte weswegen auch winzige „Effekte“ Signifikanz erreichen.

Habt Ihr jeweils Stichproben mit 32 Personen erhoben, wird der -Test signifikant, wenn sich eure Stichproben um 0.5 Standardabweichung unterscheiden. Angenommen, die Standardabweichung der Körpergröße in Deutschland beträgt 10cm. Dann erhaltet ihr ein signifikantes Ergebnis, wenn die mittlere Körpergröße in deiner Stichprobe von der deiner Kommilitonin um 5cm abweicht.

Habt Ihr aber die Körpergröße von jeweils 450 Personen gemessen, genügt ein mittlerer Unterschied von 0.13 Standardabweichungen, damit der -Test einen signifikanten Unterschied bescheinigt. Das heißt, bei Mittelwertsunterschieden von 1.3cm würde ein -Test ergeben, dass sich die Gruppen signifikant in ihrer Körpergröße unterscheiden.

Angenommen, zwei Gruppen von Menschen unterscheiden sich durchschnittlich in ihrer Körpergröße um 1.3cm. Innerhalb der Gruppen sind aber nicht alle Personen gleich groß, sondern variieren im Mittel um 10cm. Auffallen wird dieser Unterschied gewiss nicht. Und ist der Unterschied relevant? Selbst beim Basketballspielen, wo Körpergröße einen Vorteil darstellt, werden mittlere Unterschiede von 1.3cm wohl kaum von Bedeutung sein.

Bei groß angelegten Untersuchungen ist es daher empfehlenswert, vorher festzulegen, was die minimale bedeutsame Effektgröße ist und dann nicht gegen einen Nullunterschied, sondern gegen einen Unterschied von mindestens zu testen. Natürlich gehört es mittlerweile standardmäßig dazu, die Effektgröße in Ergebnisdarstellungen zu berichten.

Eine geeignete Stichprobengröße trägt also zu der Aussagekraft einer Studie bei. Einerseits bedeutet eine zu große Stichprobe, dass mehr Ressourcen in die Studie investiert wurden, als nötig gewesen wäre, da der Effekt auch mit einer kleineren Untersuchung hätte nachgewiesen werden können. Mit einer zu kleinen Stichprobe andererseits kann die Erhebung wertlos sein, da die statistischen Tests keine ausreichende Power hatten.

Wenn Du die erwartete Effektgröße kennst, z. B. aus vorherigen Untersuchungen oder theoretischen Überlegungen, kannst Du vorher eine Analyse durchführen, wie viele Probanden benötigt werden, um eine gewisse Teststärke (typischerweise 80%, noch besser sind 90%) zu erreichen. Selbst wenn Du keinen Richtwert zur Verfügung hast, kannst Du für die erwartete Effektgröße den minimalen Effekt, der bedeutsam ist und den Du daher aufdecken möchtest angeben. Es gibt einige kostenlose Programme zur Berechnung des Stichprobenbedarfs, z. B. G*Power. Mit G*Power kannst Du nicht nur solche a-priori Berechnungen anstellen für die Planung Deiner Untersuchung, sondern auch a-posteriori die Teststärke nach der Erhebung anhand der gefundenen Effektgröße ermitteln.

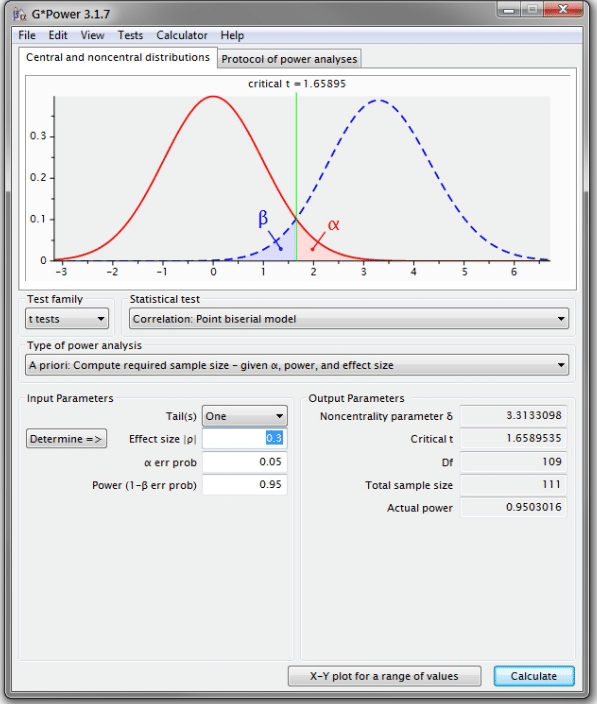
Mit G*Power können die Teststärke oder die benötigte Stichprobengröße für verschiedene statistische Verfahren ermittelt werden. Bei der Planung einer empirischen Erhebung sollte