Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Kardinalskalen: Intervallskala & Verhältnisskala
- 23. Januar 2018
- Posted by: Mika
Das höchste Skalenniveau haben Kardinalskalen, welche sich nochmals in Intervall- und Verhältnisskalen unterteilen. Für die Anwendung aller gängigen statistischen Testverfahren genügt das Intervallskalenniveau. Man spricht davon, dass sich bestimmte Parameter oder Tests ab einem bestimmten Skalenniveau anwenden lassen.
Dieses Prinzip heißt Abwärtskompatibilität, das heißt, ist ein Verfahren für ein Skalenniveau zulässig, so auch für alle höheren Skalenniveaus. Deswegen hat die Intervallskala in der empirischen Praxis größere Bedeutung als die Verhältnisskala.
Was zeichnet eine Intervallskala aus?
Dem Intervallskalenniveau liegt die Annahme zugrunde, dass die Abstände zwischen den Merkmalsausprägungen gleich sind (Gleichheit der Differenzen). Das erlaubt nicht nur größer-kleiner (oder mehr-weniger) Vergleiche zwischen den Merkmalsträgern, sondern es lässt sich sinnvollerweise über den Abstand zwischen den Merkmalsträgern sprechen.
Angenommen, Du interessierst Dich für das Persönlichkeitsmerkmal der Extraversion, und erhebst es bei Deinen Probanden mit einem Fragebogen mit 50 Fragen dazu, wie häufig sie bestimmte Verhaltensweisen zeigen. Ein Item könnte zum Beispiel so lauten: „Ich beginne gerne ein Gespräch mit anderen Personen während einer Bahnfahrt.“ und die Antwortmöglichkeiten sind 5-stufig von „nie“ bis „fast immer“. Kannst Du dann behaupten, dass eine Person mit 150 Punkten im Fragebogen doppelt so extravertiert ist wie eine Person mit 75?
Mit solchen Fragen beschäftigen sich Wissenschaftler*innen im Rahmen der Diagnostik, wenn sie über die Fragebogenkonstruktionen nachdenken. Meistens geht man davon aus, dass ein sorgfältig konstruierter Fragebogen, bei dem viele verschiedene Items zu einem gemeinsamen Punktewert aggregiert werden, Intervallskalenniveau haben. Dann könntest Du obige Frage mit „ja“ beantworten. In der Praxis ist es oft schwierig zu entscheiden, ob Daten ordinal– oder intervallskaliert sind. Sind zehn Items für einen
Fragebogen genug?
Oder ist bei Schulnoten der Abstand zwischen „sehr gut“ und „gut“ genauso groß wie zwischen „gut“ und „befriedigend“? Wahrscheinlich eher nicht, nichtsdestotrotz wird oft eine Durchschnittsnote angegeben – das ist eine Maßzahl, die Intervallskalenniveau voraussetzt.
Voraussetzungen für statistische Tests
Da viele statistische Tests Intervallskalenniveau als Voraussetzung haben, geht man im Zweifel eher von Intervallskalenniveau aus. Im Einzelfall sind solche Entscheidungen zu begründen. Testverfahren, die Intervallskalenniveau und meist auch Normalverteilung der Daten fordern, werden parametrische Tests genannt und sind sehr weit verbreitet: Dazu gehören Varianzanalysen wie der ![]() -Test, ANOVAs, Pearson-Korrelation und Regressionen.
-Test, ANOVAs, Pearson-Korrelation und Regressionen.
Für intervallskalierte Daten sind nur positive lineare Transformationen (der Form ![]() , wobei
, wobei ![]() ) zulässig, denn diese Transformationen sind abstandserhaltend: Wenn Person A bei einer IQ-Messung ein 1.5 mal so hohes Testergebnis erzielt wie Person B, bleibt der Faktor 1.5 bei einer linearen Transformation erhalten. Bei quadratischen oder logarithmischen Transformationen etwa ist das nicht der Fall.
) zulässig, denn diese Transformationen sind abstandserhaltend: Wenn Person A bei einer IQ-Messung ein 1.5 mal so hohes Testergebnis erzielt wie Person B, bleibt der Faktor 1.5 bei einer linearen Transformation erhalten. Bei quadratischen oder logarithmischen Transformationen etwa ist das nicht der Fall.
Maßzahlen
Als Maße der zentralen Tendenz und Dispersion kommen ab dem Intervallskalenniveau das arithmetische Mittel und die Varianz und Standardabweichung hinzu. Mit Histogrammen lässt sich die Verteilung von intervallskalierten Daten veranschaulichen.
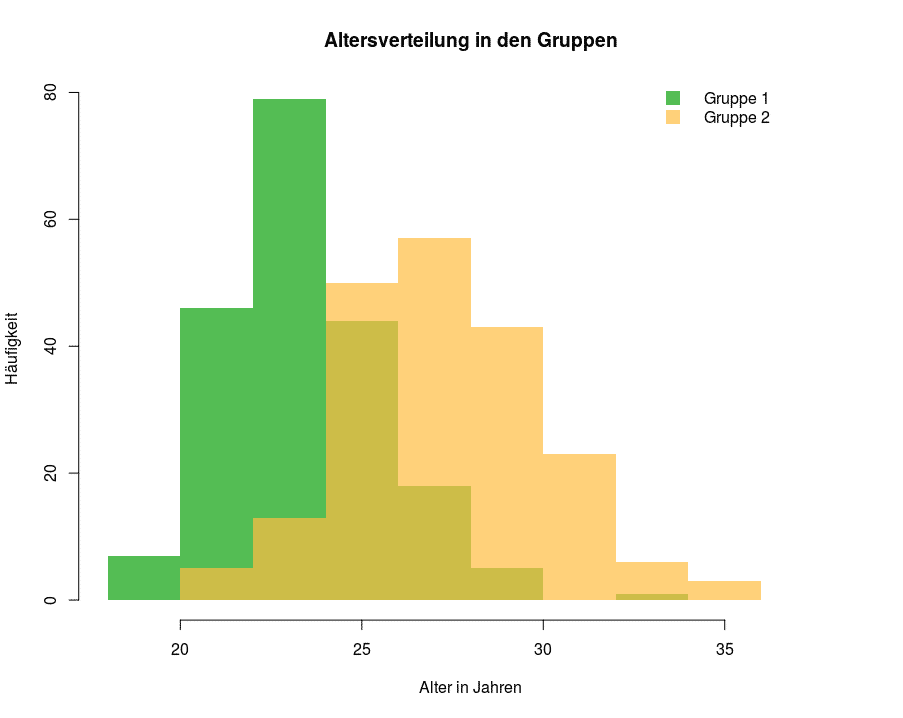
Verhältnisskalen kommen in empirischen Wissenschaften seltener vor, und zwar im Wesentlichen dann, wenn Zeitmessungen oder andere physikalische Maße (wie Länge oder Gewicht) vorliegen.
Bei Verhältnisskalen kommt die Annahme eines wohldefinierten Nullpunktes hinzu. Die Halbwertszeit eines Isotops ist beispielsweise verhältnisskaliert oder die
Reaktionszeit von Probanden bei einem Fahrtauglichkeitstest. Bei Reaktionszeitdaten gibt es aber die Besonderheit, dass sie zur besseren Interpretierbarkeit oft
logarithmiert werden, damit geht das Verhältnisskalenniveau verloren.
Die einzigen erlaubten Transformationen bei Verhältnisskalen sind multiplikative Transformation der Form ![]() für eine positive Konstante
für eine positive Konstante ![]() , damit der Nullpunkt
, damit der Nullpunkt
erhalten bleibt.
