Reliabilität

Reliabilität meint die Genauigkeit oder Zuverlässigkeit der Messung. Möchtest Du bestimmte Merkmale untersuchen, ist es zunächst wichtig, diese hinreichend genau zu messen.

Angenommen, Du hast eine Waage, um das Körpergewicht von Personen zu bestimmen. Bei Person A zeigt die Waage 70kg an, bei Person B 75kg. Die Gewichtsdifferenz beträgt also 5kg. Die Frage nach der Reliabilität dieser Messung entspricht der Frage, welcher Anteil der Unterschiede in den Messungen auf tatsächliche Gewichtsunterschiede zurückgeht. Der restliche Anteil der gemessenen Unterschiede geht auf Messfehler oder andere spezifische Anteile (z. B. die Schwerkraft am Ort der Messung) zurück.

Je größer der Anteil tatsächlicher Gewichtsunterschiede an den Messunterschieden bzw. der gemessenen Varianz, desto reliabler, also zuverlässiger, ist Deine Waage. Die Definition für die Reliabilität einer Testvariable stammt aus der Testtheorie und lautet:

(1)  

wobei für true-score, also den wahren Wert der Variable (z. B. das wahre Körpergewicht) steht. Der true-score wird nie mit absoluter Exaktheit bestimmbar sein, da es in jedem Messvorgang Messfehler gibt. Das macht die Reliabilitätsbestimmung so einer komplexen Angelegenheit: gäbe es irgendwo ein Verzeichnis mit den true-scores für ein zu messendes Konstrukt, dann könnte man ja ganz einfach vergleichen, wie genau das Messinstrument an die wahren Werte herankommt. Tatsächlich gibt es solches ein Verzeichnis natürlich nicht und die exakten true-scores sind nie bekannt – für Konstrukte wie Emotionen oder den Wert einer Immobilie gilt das natürlich umso mehr als für physikalische Maße wie die Sauerstoffsättigung oder die Wellenlängen von Licht.

Deswegen sind Reliabilitätsbestimmungen auf indirekte Verfahren angewiesen, mithilfe derer man der Messgenauigkeit auf die Schliche kommen kann: sie sollen also möglichst gute Schätzungen für die Reliabilität liefern.

Für diagnostische Messungen komplexer und nur grob umrissener Konstrukte, wie z. B. Persönlichkeitseigenschaften oder der momentanen Stimmung wird der Messfehler höher ausfallen als für physikalische Messungen, bei denen die Maßeinheit klar definiert ist. Aber auch ein Laser-Entfernungsmesser ist präziser, als wenn Du mit einem Zollstock die Länge per Hand nachmisst.

Wie kann man nun für ein Messinstrument die Reliabilität bestimmen? Und was für eine Reliabilität kann man realistischer weise von guten Instrumenten erwarten? Und andersherum, ab welcher Reliabilität ist ein Messinstrument gut genug?

Drei Ansätze haben sich zur Beantwortung der ersten Frage bewährt. Der erste Ansatz sind Stabilitätsmessungen, d. h. wiederholte Messungen über mehrere Zeitpunkte hinweg. Wenn Du die Personen mehrfach hintereinander auf die Waage stellst, und jedes Mal das gleiche Ergebnis für gleiche Personen erscheint, ist das ein Hinweis auf Reliabilität. Denn dann ist das angezeigte Gewicht nicht nur ein zufälliger Wert, sondern kann sinnvoll zwischen Personen differenzieren.

Der zweite Ansatz ist eine Konsistenzmessung. Diagnostische Testverfahren setzen sich normalerweise aus mehreren Bestandteilen zusammen, ein Fragebogen z. B. aus verschiedenen Items. Sind alle Items innerhalb eines Probanden relativ ähnlich, aber über die Probanden hinweg unterschiedlich beantwortet, spricht man von hoher interner Konsistenz des Instrumentes. Schließlich kann man die Reliabilität eines Messinstrumentes auch noch im Vergleich mit einem äquivalenten Test, einem sogenannten Paralleltest, bestimmen.

Aus diesen Ausführungen geht schon ein sehr wichtiger Aspekt hervor, den man unbedingt beachten muss: Während Messwerte für gleiche Personen möglichst ähnlich ausfallen sollen, müssen sie sich zwischen den Personen unterscheiden. Kurz ausgedrückt: Für Reliabilität bedarf es Merkmalsvarianz.

Auf die Bedeutsamkeit von Merkmalsvarianz und analog dazu der Stimulusvarianz gehen wir schon an anderer Stelle ein. Allerdings lohnt hier ein kurzer Exkurs, da Varianz nicht nur für das Konzept der Reliabilität von fundamentaler Bedeutung ist. Große Teile der Statistik basieren auf Varianzanalysen, seien es ANOVAS, Regressionsanalysen oder Mehrebenenmodelle; das Ziel ist immer, Unterschiede in der interessierenden Variable aufzuklären. Je nach Kontext heißt diese die abhängige Variable, Kriteriumsvariable, Testvariable oder endogene Variable. Und zwar gelingt dies mithilfe von Unterschieden in den erklärenden (prädiktiven/unabhängigen) Variablen.

Wenn es keine Varianz in den Merkmalen gibt, kann auch nichts erklärt werden. Das ist ein simples Konzept, das aber oft übersehen wird, weil größere Varianz oft mit größeren Standardfehlern assoziiert ist. Genauso wie im obigen Pflanzenbeispiel verhält es sich mit der Messvarianz für die Reliabilität. Wenn die Waage für alle Personen das gleiche Gewicht anzeigt, ist die Reliabilität bei null. Genauso könnte die Waage immer „Error“ oder eine beliebige Zahl im Display anzeigen, wenn sie nicht zur Differenzierung der Probanden beiträgt, ist sie wertlos.

Aber führen wir diesen Gedanken einmal weiter. Die Reliabilität hängt nämlich tatsächlich nicht nur vom Messinstrument, sondern immer auch von der Stichprobe ab. Wenn Deine Stichprobe aus lauter gleich großen, ähnlich gebauten Personen besteht, liegen ihre wahren Körpergewichte sehr nah beieinander. Es gibt also recht wenig true-score-Varianz, die durch die Waage aufgedeckt werden kann. Entsprechend werden Messunterschiede zu einem größeren Teil durch Messfehler und spezifische Anteile zustande kommen. Der Anteil der gemessenen Varianz, der auf wahre Gewichtsunterschiede zurückgeht, ist also relativ klein, denn die wahren Unterschiede sind kaum größer als die Genauigkeitsgrenze der Waage. Hast Du hingegen eine extrem heterogene Stichprobe bestehend aus Kindern und Menschen ganz unterschiedlicher Statur und reichen die wahren Körpergewichte von 20kg bis 120kg, gibt es sehr viel erklärbare Varianz. Mit dieser Stichprobe fällt die Reliabilität der identischen Waage also deutlich höher aus. Die Waage misst sehr große Unterschiede und diese gehen zu einem großen Anteil auf tatsächliche Gewichtsunterschiede zurück. Reliabilität ist also eine Eigenschaft der Messung, und keine Eigenschaft des Messinstrumentes, auch wenn es oft der Einfachheit halber so dargestellt wird.

Retestreliabilität

Eine Möglichkeit, um die Reliabilität eines Tests zu bestimmen, ist seine Stabilität zu bestimmen. Die Testwiederholung bezeichnet man als Retest. Man wiederholt also den Test zu einem zweiten Zeitpunkt mit den gleichen Probanden und bestimmt die Reliabilität des Tests zum ersten Zeitpunkt aus der Kovarianz der beiden Messzeitpunkte als

   

Wenn Du die Reliabilität eines Instrumentes über seine Stabilität, also mithilfe der Retest-Methode bestimmst, fließen einige zentrale Annahmen in die Rechnung. Zum einen setzt die Retestreliabilität voraus, dass das Merkmal zeitlich absolut stabil ist. Das heißt, Personen verändern sich hinsichtlich dieses Merkmales nicht über die Zeit. Bei unserem Gewichtsbeispiel wäre diese Annahme verletzt, es kann beträchtliche Gewichtsschwankungen über die Zeit geben. Zum anderen nimmt man an, dass es keine Testwiederholungseffekte gibt. Bei Intelligenztests oder Denkaufgaben könnte diese Annahme problematisch sein, da man Aufgaben evtl. besser bearbeitet, wenn man sie schon kennt. Bei Aufgaben, in denen es um Bearbeitungs- oder Reaktionsgeschwindigkeit geht, sind Testwiederholungseffekte eher vernachlässigbar.

Drittens fließt in die Retestreliabilität die Annahme ein, dass es keine Probanden-spezifischen Fehler gibt, also dass die Fehler bei der Testwiederholung nicht systematisch mit den Fehlern im Test zum ersten Zeitpunkt zusammenhängen.

Für die Wahl eines günstigen Zeitintervalls zwischen beiden Messzeitpunkten stehen sich die ersten beiden Annahmen gegenseitig im Wege: Während für die Annahme der Stabilität möglichst kurze Zeitintervalle geeignet sind, da über kurze Zeit hinweg weniger Veränderungen im Merkmal zu erwarten sind, ist für die Vermeidung von Übungs- und Erinnerungseffekten ein großer Abstand zwischen den Testungen geeignet.

Besonders angemessen ist die Retest-Methode, wenn stabile Merkmale gemessen werden sollen, wie z. B. Persönlichkeitseigenschaften. Bei Leistungstests, die durch Übung besser bearbeitet werden können und Zustandsmessungen sollte man auf andere Methoden zur Reliabilitätsmessung zurückgreifen.

Testhalbierungsmethode und interne Konsistenz

Um sich den Aufwand einer Testwiederholung zu sparen, kannst Du anstelle von zwei Testergebnissen zu verschiedenen Messzeitpunkten auch einfach das Testergebnis der ersten Testhälfte mit dem Ergebnis der zweiten Testhälfte vergleichen.

Bei Reaktionszeitaufgaben wäre das also die durchschnittliche Reaktionsdauer bei der ersten Hälfte der Aufgaben und der zweiten Hälfte; bei Leistungstests die Anzahl der richtig gelösten Aufgaben in der ersten und zweiten Hälfte, usw.

Aus den so erhaltenen Testhälftenergebnissen bestimmst Du die Varianz und die Kovarianz und berechnest den Anteil der Kovarianz an der Varianz des Gesamttests. Es gibt verschiedene Möglichkeiten, den Test in zwei Hälften zu teilen. Die oben beschriebene Split-Half-Methode, die zufällige Aufteilung der Items oder der Odd-Even-Split, also alle geradzahligen Items in der einen und alle ungeraden Items in der anderen Hälfte, gehören zu den gängigsten Aufteilungen.

Genau genommen berechnet man mit der Testhalbierungsmethode nicht die Reliabilität des Tests, sondern die Reliabilität nur einer Testhälfte. Und es gilt die generelle Regel, dass Tests umso reliabler sind, je mehr Items sie umfassen. Das kann man mithilfe der Überlegung erkennen, dass jedes Item einen Teil vom Konstrukt misst und einen spezifischen Anteil. Die spezifischen Anteile sind aber über alle Items hinweg unkorreliert und voneinander unabhängig. Das heißt sie mitteln sich bei Aggregation aller Items aus, während sich die wahren Anteile aufaddieren.

Das Prinzip Fragebögen mit möglichst vielen Items auszustatten, steht übrigens im Widerspruch zu den Nebengütekriterien der Ökonomie und Zumutbarkeit, da Probanden oft keine Lust haben, seitenweise Fragebögen auszufüllen. Der Trend, breite Konstrukte nur mit drei Items abzufragen, ist aber unter Reliabilitätserwägungen problematisch.

Auf die Testhalbierungsmethode angewendet, ergibt sich daraus, dass eine Testhälfte eine geringere Reliabilität als der gesamte Test hat. Dies kann man mit einer Korrekturformel berücksichtigen, indem man die Reliabilität des gesamten Tests hochrechnet. Die Formel heißt Spearman-Brown-Formel. Die Reliabilität des gesamten Tests Rel(S) kann aus der Reliabilität einer Testhälfte hochgerechnet werden als:

   

Betrachten wir die Konsistenzberechnung mal an einem Beispiel: Der PANAS – kurz für Positive Affect and Negative Affect Scale – ist ein häufig eingesetzter Fragebogen zum momentanen Affekt. Er soll die Ausprägung von positiver und negativer Stimmung mit 20 Items messen: zu je 10 positiv und negativ besetzten Adjektiven sollen die Probanden auf einer fünfstufigen Likert-Skala von „gar nicht“ bis „äußerst“ ihre aktuellen Empfindungen beschreiben.

Ausschnitt aus der Skala zur Bestimmung des positiven Affekts.

Du erhebst die positive Stimmung von 200 Probanden mit 6 Items der Skala zum positiven Affekt und möchtest die Reliabilität der Messung bestimmen. Da die augenblickliche Stimmung per Definition kein besonders zeitlich stabiles Konstrukt ist, entscheidest Du Dich für eine Konsistenzanalyse.

Die Antwort „überhaupt nicht“ wird mit 1, die Antwort „äußerst“ mit 5 und alle Zwischenwerte mit den entsprechenden Zahlen dazwischen kodiert. Der minimale Wert, also der Wert, wenn die Probanden überall „überhaupt nicht“ zur Beschreibung ihrer positiven Empfindungen ankreuzten ist 6 und der Maximalwert beträgt 30.

Bei der Testhalbierungsmethode teilst du den Test zufällig in zwei Hälften auf. Für die erste Hälfte erhältst Du aktiv, begeistert, stolz und die zweite Hälfte setzt sich aus den Items interessiert, freudig erregt und stark zusammen.

Unter einigen testtheoretischen Annahmen, auf die wir hier nicht näher eingehen, ergibt sich die Reliabilität einer Testhälfte aus der Korrelation zwischen beiden Testhälften.

   

In Deinem Zahlenbeispiel erhältst Du eine Korrelation von 0.83 zwischen beiden Testhälften. Wie oben beschrieben, ist die Reliabilität für die Gesamtskala größer als nur für eine ihrer Hälften.

Deren Reliabilität ergibt sich dann also mithilfe eines Korrekturfaktors:

   

Da die Reliabilität eines Tests den Anteil gemeinsamer Varianz mit einem anderen Test ausdrücken an der Gesamtvarianz ausdrückt, ist der Wertebereich für Reliabilitätskoeffizienten zwischen 0 und 1. Wobei 0 absolute Unreliabilität und 1 perfekte Reliabilität ausdrücken würde.

Um die Reliabilitätskoeffizienten einordnen zu können, gibt es einige Faustregeln, ab wann man guten Reliabilitätsmessungen ausgehen kann. Die kritische Schwelle, ab der ein Messinstrument noch akzeptabel ist, wird meist bei 0.7 angesehen.

Die Idee der Testhalbierung lässt sich weiterspinnen, indem man die Testhälften wiederum halbiert usw., bis der Test in seine kleinsten Bestandteile, seine Items zerlegt ist. Zwischen all diesen Items lässt sich die Korrelation berechnen und aus diesen Einzelkorrelation die Reliabilität des gesamten Tests hochrechnen.

Etwas genauer funktioniert das so: Die Varianz des Testscores lässt sich zerlegen in die Summe aus Item-Varianzen und die Kovarianzen zwischen allen paarweisen Itemkombinationen:

   

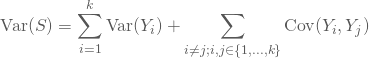
Dabei ist Var() die Varianz des i-ten Items. Insgesamt gibt es Items.

Das einfache Konsistenzmaß ist der Anteil der Kovarianzen zwischen den Items an der Gesamtvarianz der Testscores. Das lässt sich aus der Überlegung herleiten, dass die interne Konsistenz die Frage nach der Gemeinsamkeit über alle Items hinweg beantworten soll. Wie viel von der Gesamtvarianz des Tests lässt sich also auf Gemeinsamkeiten zwischen den Items zurückführen, und wie viel davon sind itemspezifische Reste?

Je größer die Kovarianzen, also die gegenseitige Abhängigkeit der einzelnen Items untereinander, desto ähnlicher sind sich die Items untereinander. Ähnlich meint in diesem Fall, dass es innerhalb der Probanden ähnliche Ankreuzmuster gibt.

Um eine Korrekturformel ergänzt, ist dies das bekannte Maß der internen Konsistenz, Cronbachs :

   

Dabei ist Var() die Varianz des i-ten Items und Var(Y) ist die Gesamtvarianz des Testscores.

Cronbachs ist eine Schätzmethode für die Reliabilität eines Tests. Es misst die Ähnlichkeit der Items untereinander, oder noch genauer, ob Probanden tendenziell alle Items ähnlich bewerten. Es ist ein sehr häufig eingesetzter Index, in Gütebewertungen von diagnostischen Tests findet sich meistens eine Angabe zu Cronbachs .

Betrachten wir nochmal unser obiges Beispiel. Anstatt den Test in zwei zufällige Hälften einzuteilen, möchten wir jetzt die interne Konsistenz über die einzelnen Items hinweg ausrechnen:

In der untenstehenden Graphik dargestellt sind für alle Itempaare die Kovarianzen dargestellt. Je dunkler sie eingefärbt sind, desto höher ist die Kovarianz zwischen zwei Items. Der Anteil der gemeinsamen Varianz an der Gesamtvarianz des Testscores gibt die interne Konsistenz an.

Mit einem Statistikprogramm kannst Du für Deine erhobenen Daten die interne Konsistenz für deinen Test zum positiven Affekt bestimmen. Als Ergebnis liefert Dir z.B. das Programm R ein Cronbachs Alpha von 0.92. Anhand der Tabelle mit den Faustregeln erkennst Du, dass Deine Erhebung eine sehr gute interne Konsistenz hatte und Du also von einer guten Reliabilität des Testinstruments ausgehen kannst. Außerdem beinhaltet die Ausgabe für die Berechnung von Cronbach‘s Alpha noch eine Tabelle, die in etwa wie die untenstehende Tabelle aussieht:

Die Tabelle schlüsselt für die einzelnen Items nochmal einige Kennwerte aus, die erkennen lassen, wie konsistent das jeweilige Item mit dem gesamten Test ist. Neben Mittelwert und Standardabweichung für die Items findest Du die korrigierte Whole-Part-Korrelation, die ausdrückt, wie sehr der Itemscore mit dem Testscore korreliert, wenn du das entsprechende Item aus dem Testscore herausrechnest. Außerdem steht dort noch der Wert Cronbachs Alpha, den der Test hätte, wenn man das entsprechende Item entfernt. Wie Du siehst, verschlechtert sich Cronbachs Alpha meist, wenn ein Item herausgenommen wird. Nur das Item „stolz“ liefert keinen inkrementellen Beitrag zur internen Konsistenz: insgesamt scheint dieses Item am meisten von den anderen Items abzuweichen: Der Standardfehler sinkt, wenn man es entfernt, und die durchschnittliche Korrelation zwischen je zwei Items würde noch zunehmen. Von allen Items hat „stolz“ die niedrigste Whole-Part-Korrelation, mit .58 ist es immer noch eine hohe Korrelation und damit kein Grund, das Item aus dem Test zu entfernen.

Allerdings ist eine hohe Konsistenz möglicherweise nicht immer erstrebenswert oder umsetzbar, und sagt nur etwas darüber aus, dass die Items untereinander sehr ähnlich sind. Viele redundante oder ähnlich lautende Items erhöhen die interne Konsistenz eines Tests. Aber damit tragen sie vielleicht nicht unbedingt zu einer präziseren Messung bei.

Bei sehr homogenen, eng gefassten Konstrukten ist die interne Konsistenz eine geeignete Schätzmethode für die Reliabilität. Bei heterogenen Konstrukten, die sich aus verschiedenen Facetten zusammensetzen, ist interne Konsistenz möglicherweise gar nicht erwünscht. Schließlich soll der Fragebogen dann verschiedene, voneinander nicht zwangsläufig abhängige Aspekte des Merkmals erfassen.

Paralleltest-Methode

Steht ein zweiter Test für das gleiche Merkmal zur Verfügung, kannst Du Deine Probanden mit beiden Tests untersuchen und die Übereinstimmung zwischen beiden Testformen als Maß für die Reliabilität berechnen. Auch hier kann es zu Übungseffekten zwischen beiden Testformen kommen und in der Methode steckt die implizite Annahme, dass bei Tests exakt das gleiche messen.

Für viele Merkmale ist es schwierig eine strenge Parallelform zu entwickeln, da es gerade für eng umschriebene Konstrukte nicht beliebig viele geeignete Items gibt. Wenn die Items nahezu oder vollständig identisch sind in beiden Testformen, ist diese Reliabilitätsbestimmung dasselbe wie die Retest-Methode.

Für alle diese Methoden gilt, dass die resultierenden Reliabilitätskennwerte zwischen 0 und 1 liegen. Höhere Werte bescheinigen eine höhere Reliabilität. Es gilt die Faustregel, dass Reliabilitäten ab .80 akzeptabel und ab .90 gut sind.