Bootstrapping

Bootstrapping ist eine Methode, um Konfidenzintervalle für bestimmte Stichprobenkennwerte oder Effektgrößen zu berechnen. Konfidenzintervalle sind bestimmte Bereiche, innerhalb derer sich der „wahre Wert“ mit hoher Wahrscheinlichkeit befindet. Da der Alpha-Fehler typischerweise bei 5% liegt, umfassen Konfidenzintervalle meist den Bereich 95%-iger Wahrscheinlichkeit. Das heißt, mit 95%-iger Sicherheit liegt der gesuchte Wert innerhalb des Konfidenzintervalls. Die Irrtumswahrscheinlichkeit, also dass der wahre Wert außerhalb dessen liegt, ist dann die Gegenwahrscheinlichkeit von 5%.

Der Vorteil von Bootstrapping ist, dass diese Methode keine Verteilungsannahme trifft. Es handelt sich also um ein non-parametrisches Verfahren und kann auch angewandt werden, wenn Normalverteilungsannahmen des Modells nicht oder nur zweifelhaft erfüllt sind. Des Weiteren ist es ein robuster, einfacher Computer-Algorithmus, der je nach Implementierung nur mäßig viel Rechenzeit erfordert. Bootstrapping basiert auf Resampling: das heißt aus den gegebenen Daten werden wiederholt Stichproben gezogen.

Für unabhängige Zufallsziehungen sind die Ergebnisse mindestens genauso akkurat wie die Berechnung von Konfidenzintervallen mit analytischen Verfahren, also Berechnungen mithilfe des Standardfehlers. Bootstrapping kann für beliebige Parameterschätzungen angewandt werden, in manchen Fällen ist es allerdings sinnvoller als in anderen. Vor allem, wenn Du eine Statistik bestimmen möchtest, für die die Normalverteilungsannahme nicht oder nur zweifelhaft erfüllt ist, ist das Bootstrap-Verfahren empfehlenswert. Die Normalverteilungsannahme bezieht sich auf den Stichprobenkennwert: für Mittelwerte ist diese Annahme zum Beispiel erfüllt. Damit ist gemeint, wenn du theoretisch unendlich viele Stichproben der Größe aus der gleichen Population ziehen würdest, wären der Mittelwerte normalverteilt um den „wahren“ Populationsmittelwert mit dem Standardfehler als Streuung.

Bei Anteilen (damit ist so etwas gemeint wie prozentuale Aussagen über die Bevölkerung; z. B. zu Parteipräferenzen), Korrelationskoeffizienten, aber auch bei Effektgrößen in Pfadanalysen ist die Annahme der Normalverteilung nicht oder höchstens zweifelhaft erfüllt, sodass dann eine Berechnung des Konfidenzintervalls mithilfe von Bootstrapping zu bevorzugen ist.

Auch bei kleinen Stichprobengrößen bietet sich das Verfahren an.
Der Name Bootstrapping geht übrigens zurück auf das englische Sprichwort, sich an den eigenen Füßen aus dem Sumpf ziehen an. Es spielt darauf an, dass man bei diesem Verfahren den Bedarf an etlichen weiteren Stichproben umgeht, indem es immer Stichproben aus der einen gegebenen Stichprobe zieht.

Wie funktioniert Bootstrapping nun?

Die grobe Idee ist leicht zu verstehen. Aus der ursprünglichen Stichprobe mit Datenpunkten wird mit Zurücklegen eine Stichprobe der Größe gezogen. Das heißt diese Stichprobe besteht aus Einträgen des Datensatzes, aber manche Datenpunkte sind mehrfach vertreten, andere wurden gar nicht gezogen. Diese Ziehung wird sehr oft wiederholt, typischerweise gibt es zwischen 1.000 und 10.000 Iterationen. Für jede dieser tausenden -elementigen Stichproben werden dann die interessierenden Kennwerte berechnet:
Das kann ein Odds Ratio, ein Mediatoreffekt, oder die vorhergesagten Werte einer Regression sein.
Das 95%-Konfidenzintervall wird dann aus all diesen Stichproben bestimmt: Und zwar schließt es 95% aller so erhaltenen Parameterschätzungen ein, die jeweils 2,5% größten und kleinsten Parameterschätzungen der zahlreichen bootstrap-Stichproben werden ausgeschlossen.

Veranschaulichen wir uns den Algorithmus an zwei Beispielen.
Zunächst stellen wir uns vor, Du hast die Wasserqualität von 25 verschiedenen Gewässern in Deutschland bestimmt, und zwar auf einer Skala von 0 bis 100, wobei höhere Werte eine bessere Wasserqualität bescheinigen. Du möchtest ein Konfidenzintervall für die mittlere Wasserqualität (das arithmetische Mittel) mithilfe des Bootstrap-Verfahrens bestimmen. Dazu gehst du wie folgt vor:

• Du wählst die Anzahl der Iterationen: also wie viele Stichproben gezogen werden sollen. Da 1000 als gängige Anzahl oft verwendet wird, entscheidest Du Dich dafür.
• Nun generierst du die Bootstrap-Stichproben wie folgt: Aus deiner ursprünglichen Stichprobe ziehst du 1000-mal weitere Stichproben, die jeweils auch die Größe 25 haben. Und zwar mit Zurücklegen. Ohne Zurücklegen wäre dieses Vorgehen witzlos, da dann jede Stichprobe exakt der Original-Stichprobe entsprechen würde. Mit Zurücklegen aber werden manche Fälle bzw. Datenpunkte (in Deinem Fall, Gewässer) mehrfach gezogen oder andere gar nicht, und so entstehen unterschiedliche Bootstrap-Stichproben. Es gibt auch Modifikationen des Algorithmus, in denen die Bootstrap-Stichproben weniger als 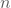(in Deinem Fall 25) Elemente haben.
• Für jede der 1000 Bootstrap-Stichproben berechnest du den interessierenden Stichprobenkennwert. In dem Beispiel ist das der simple Fall des Mittelwerts, aber du kannst beliebige Statistiken für die Bootstrap-Stichproben bestimmen: wie oben schon beschrieben eignet sich Bootstrap für Odds-Ratio, Perzentile, Anteile, Pfadkoeffizienten, Mediationsanalysen oder andere denkbare Stichproben- oder Verteilungskennwerte.
• Du hast also nun 1000 verschiedene Mittelwerte: einen für jede der Bootstrap-Stichproben. Diese Dichtefunktion dieser Mittelwerte ist in der Graphik dargestellt.

  

• Die Idee für das weitere Vorgehen ist eigentlich ganz simpel: Aus den 1000 Mittelwerten bestimmst Du jeweils die 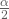(für ein 95%-Vertrauensniveau ist 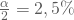) kleinsten und größten Mittelwerte. Also die besonders extremen Mittelwerte am Rande der Verteilung. Und diese Perzentile, also das 2.5% und das 97.5% Perzentil bilden dann die Grenzen Deines Konfidenzintervalles. Die Perzentile, also die Grenzen des Konfidenzintervalls, sind auch in der untenstehenden Graphik durch die gestrichelten, gelben Linien gekennzeichnet.

Fertig ist die Berechnung des Konfidenzintervalls. In einem zweiten Beispiel hast Du das monatliche Einkommen von 81 Mitarbeiterinnen und Mitarbeitern in einem Unternehmen erhoben und führst das Bootstrap-Verfahren genauso wie in dem Beispiel mit der Wasserqualität durch.

Die Dichteverteilung der Bootstrap-Mittelwerte sieht hier sehr ungewöhnlich aus: Statt annähernd der Glockenkurve einer Normalverteilung zu folgen, ist diese Verteilung mehrgipflig und sehr linkssteil. Das ist ein Hinweis darauf, dass die Variable Einkommen in der zugrunde liegenden Stichprobe auch sehr linkssteil verteilt ist: es gibt also viele Personen mit einem niedrigen Einkommen und deutlich weniger Personen mit hohem Einkommen.

Damit diese Berechnungen effizient ablaufen können und möglichst wenig Rechenaufwand benötigen, gibt es verschiedene leichte Abwandlungen des Algorithmus, die an dieser Stelle nicht näher besprochen werden. Die meisten Statistikprogramme wie R oder SPSS erlauben die Bestimmung von Konfidenzintervallen mit Bootstrap-Verfahren.