GARCH-Modelle

In der Regel interessiert uns in Zeitreihenanalysen in erster Linie, welche Energieverbräuche, wie viele Verkäufe eines Unternehmens oder welche Temperatur in der Atmosphäre über die Zeit zu erwarten ist und wie sie in Zukunft aussehen könnten. Dafür wird in Zeitreihenanalysen der bedingte Mittelwert einer Zeitreihe geschätzt. Es kann aber auch sein, dass dich in erster Linie nicht die Anzahl Deiner Verkäufe interessiert, sondern inwieweit die Verkäufe eines Unternehmens über die Zeit schwanken. Vor allem in der Finanz- oder in der Versicherungswirtschaft interessiert man sich, wie stark bspw. Aktienkurse oder Risiken bestimmten Schwankungen unterliegen bzw. wie volatil diese sind. Dafür ist es notwendig, insbesondere die Heteroskedastizität von Zeitreihen zu berücksichtigen. Aktienkurse folgen in der Regel keiner zufälligen oder gar gleichmäßigen Volatilität, sondern Phasen geringer Kursschwankungen folgen wiederum Phasen intensiver Kursschwankungen. Aktienkurse oder Börsenindizes lassen über die Zeit oft Volatilitätscluster erkennen. Diese zu identifizieren und korrekt zu beschreiben ist das wesentliche Merkmal von (general) autoregressive conditional heteroscedasticity-Modellen, sogenannte (G)ARCH-Modelle.

ARCH oder GARCH schätzen die Volatilität oder Varianz einer Zeitreihe und nicht deren Mittelwerte auf der Grundlage vergangener Veränderungen oder Varianz. Um festzustellen, ob Deine Zeitreihe autoregressives Verhalten der Varianz erkennen lässt, hilft wie bei allen Zeitreihen ein Blick in deren Autokorrelationsfunktion. Allerdings sollte sich keine Autokorrelation des Mittelwerts Deiner Veränderungen in der Zeitreihe, sondern vor allem im zweiten Moment der Zeitreihe, das heißt in der Varianz der Veränderungen zeigen. Dann erkennst Du in der Autokorrelation deiner Beobachtungen sogenanntes volatility clustering oder conditional heteroscedasticity, die mithilfe von (G)ARCH-Prozessen beschrieben werden können. In GARCH-Modellen wird Heteroskedastizität nicht als Problem, sondern zum Kern der Schätzung gemacht, indem die Heteroskedastizität explizit als Varianz modelliert wird. Vereinfacht gesagt, wird dafür in ARCH-Modellen die Volatilität zum Zeitpunkt t auf die Returns der Zeitreihe zurückgeführt. Returns beschreiben in der Finanz- und Versicherungswirtschaft die relative Veränderung in Kursen oder Indizes in der Form . Das Wesen von ARCH und GARCH-Modellen ist die Beschreibung jener relativer Veränderungen und der Volatilität der Veränderung. In GARCH-Modellen kommt hinzu, dass die Volatilität nicht nur von den vorhergehenden returns , sondern von der eigenen, vergangenen Varianz über die Zeitreihe bestimmt wird. Allgemein werden also analog zu ARMA()-Modellen, GARCH()-Modelle identifiziert, wobei eben nicht das bedingte Mittel, sondern die bedingte Varianz in Abhängigkeit der relativen Veränderungen und historischen Varianz gesucht wird. In der Regel finden GARCH(1,1)-Modelle Anwendung, da viele Zeitreihen, vor allem auf Finanzmärkten über die Beobachtungen der Vorperiode zum Zeitpunkt -1 zurückgeführt werden können. In der einfachsten Form, können GARCH(1,1)-Modelle entsprechend folgendermaßen beschrieben werden:

   

Stell Dir bspw. vor, Du willst die Veränderungen in Deinen Gewinnen analysieren und beschreiben, wie stark diese schwanken. Dafür siehst Du Dir die relative Veränderung in Deinen täglichen Gewinnen an. Das GARCH(1,1)-Modell schätzt nun die Volatilität bzw. Varianz in Deinen täglichen Gewinnen, indem Sie die Varianz derer auf die relative Veränderung in Deinen Gewinnen und die Varianz zum Zeitpunkt -1 zurückführt.

Ein Ausschnitt der ersten zehn Tage des vergangenen Geschäftsmonats zeigt Dir folgende relative Veränderungen Deiner Gewinne:

Tag 1	Tag 2	Tag 3	Tag 4	Tag 5	Tag 6	Tag 7	Tag 8	Tag 9	Tag 10
-0,013	-0,009	-0,02	-0,037	-0,035	-0,073	-0,27	0,029	0,13	-0,058

Du stellst eine starke Schwankung in Deinen Gewinnveränderungen zwischen 6 und 9 fest und vermutest an diesen Tagen volatility clustering.
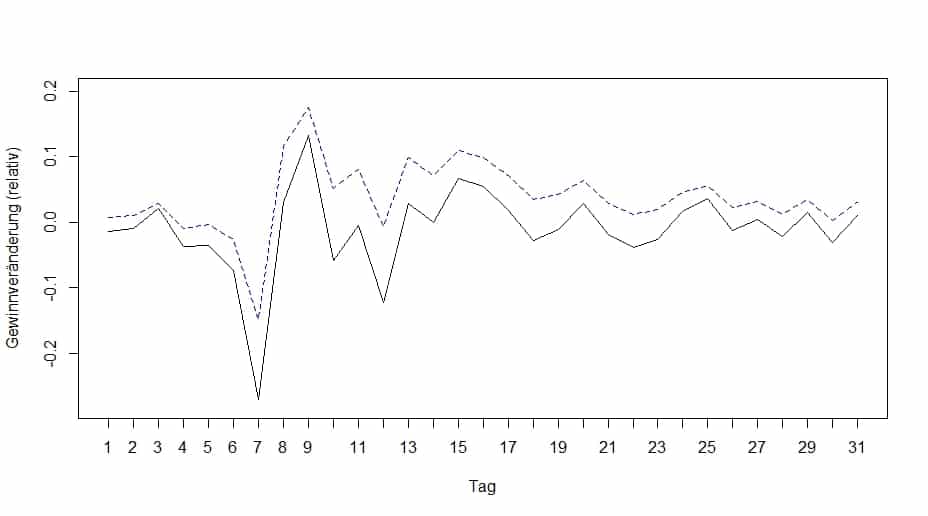
Der untenstehende Graph zeigt die relative Veränderung Deiner Gewinne für jeden Tag des letzten Monats und Dein Verdacht auf geclusterte Volatilität an bestimmten Tagen bestätigt sich. Mithilfe eines GARCH(1,1)-Modells beschreibst Du die Varianz in Deinen Daten korrekt, indem Du die Volatilität in Deinen Gewinnveränderungen berücksichtigst. Die gestrichelte Linie zeigt die geschätzte Standardabweichung zu jedem Tag. Wie Du sehen kannst, kann das GARCH(1,1) sehr gut die Volatilität oder Varianz bzw. Standardabweichung in Deinen Gewinnveränderungen nachvollziehen.

Wie in allen autoregressiven Modellen ist es Dir auch mit GARCH(1,1)-Modelle möglich, die Schwankungen in den kommenden Tagen auf der Grundlage der vergangenen Beobachtungen und Varianz in Deinen Daten unter Unsicherheit vorherzusagen.