Autoregressive Modelle (AR-Modelle)

Beobachtungen, die über die Zeit von sich selber abhängen, nennt man autoregressiv oder seriell korreliert. Autoregressive Zusammenhänge findest Du in vielen Modellen abgekürzt als AR-Modelle wieder. In aller Regel werden Dir diskrete Zeitreihen vorliegen. Das heißt, Zeitreihen werden in Minuten, Stunden, Tagen, Jahren oder anderen eindeutig abzählbaren Intervallen gemessen. Autoregressive Modelle beschäftigen sich dann vor allem mit der Frage, inwieweit die Beobachtung zum Zeitpunkt (in Stunden, Tagen oder Jahren) von der Vergangenheit abhängen. Es kann zum Beispiel sein, dass Beobachtungen heute (oder in diesem Jahr) nur von Beobachtungen gestern (oder des vergangenen Jahres) abhängen. Es kann aber auch sein, dass heutige Beobachtungen von Beobachtungen beeinflusst werden, die weit in der Vergangenheit liegen. Dabei kann es auch sein, dass Beobachtungen, die weit in der Vergangenheit liegen, einen geringeren Einfluss haben, als welche aus der jüngeren Vergangenheit. Deine Aufgabe ist es dann, ein Modell zu finden, das die Zusammenhänge über die Zeit am besten beschreibt. Werden Deine heutigen Beobachtungen von vielen Beobachtungen in der Vergangenheit beeinflusst, dann hast Du es mit hoch autoregressiven Modellen zu tun. Das kann auch allein dadurch bedingt sein, dass Dir hochaufgelöste Zeitreihen vorliegen, die bspw. jede Minute den Energieverbrauch eines Haushalts oder die Temperatur in der Atmosphäre messen. Fasst Du die Beobachtungen auf monatliche oder jährliche Beobachtungen zusammen, wird sich wahrscheinlich auch die serielle Korrelation, also die Abhängigkeit der Beobachtungen über die Zeit verringern, da die Zeitabstände zwischen den Beobachtungen größer werden.

Die einfachste Form eines autoregressiven Modells ist also, wenn sich Deine Beobachtung zum Zeitpunkt nur von der Beobachtung zum Zeitpunkt -1 abhängt. Ein solches Modell wird auch als autoregressives Modell der ersten Ordnung oder AR(1) beschrieben. Natürlich kann ein autoregressives Modell unbestimmt viele Ordnung in AR()-Modellen erreichen. Viele Zeitreihen werden jährlich erfasst oder beschrieben, sodass autoregressive Modelle geringer Ordnung oftmals ausreichen, um den Einfluss vergangener Beobachtungen schätzen zu können. Deshalb beschränken wir uns auf die Einführung eines AR(1)-Modells.

Stell dir beispielsweise vor, Du willst Deine Verkäufe der kommenden Tage auf der Grundlage Deiner Verkäufe in den letzten Tagen schätzen. Du nimmst an, Deine Verkäufe folgen einem AR(1)-Prozess und Du schätzt Deine Verkaufszahlen zum Tag auf der Grundlage des vergangenen Tages -1. Deshalb wird auch als lag-Variable bezeichnet, da Deine vergangenen Verkäufe verzögert auf Deine aktuellen und zukünftigen Verkäufe wirken. Du legst nun die Verkaufszahlen der vergangenen zehn Tage für Deine Schätzung zugrunde:

Tag 1	Tag 2	Tag 3	Tag 4	Tag 5	Tag 6	Tag 7	Tag 8	Tag 9	Tag 10
3	4	7	9	8	7	4	2	3	4

Dann folgen Deine Verkäufe zum Tag einem AR(1)-Prozess, die auf den vergangenen Verkäufen zum Zeitpunkt -1 und den verbleibenden Fehler des Prozesses zurück:

   

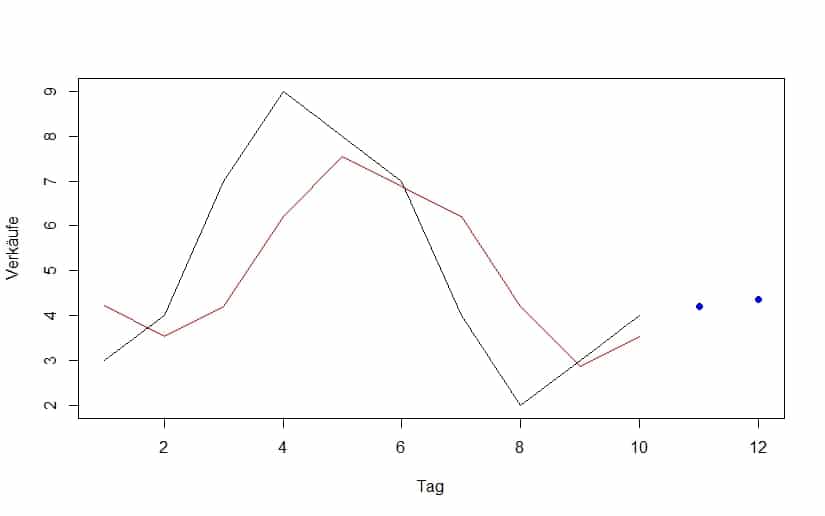
Dies gilt, wenn Dein Mittelwert von , wie im obigen Beispiel. Das Ergebnis Deiner Schätzung zeigt untenstehender Graph. Der schwarze Verlauf zeigt Deine tatsächlichen Verkäufe, der rote Verlauf zeigt Deine geschätzten Verkäufe, wenn wir annehmen, Deine Verkäufe folgen einem AR(1)-Prozess, in dem Deine vergangenen Verkäufe verzögert auf Deine aktuellen Verkäufe wirken. Die Verzögerung macht sich in Deiner Schätzung bemerkbar und die Schätzung folgt nicht exakt Deinen tatsächlichen Verkäufen. Deine Verkäufe zum zweiten Tag sind eigentlich eine Funktion der Verkäufe zum vergangenen ersten Tag. Damit ist Dir aber auch gleichzeitig möglich, Deine Verkäufe am elften Tag auf der Grundlage Deiner Verkäufe vom zehnten Tage zu schätzen und mit zunehmender Unsicherheit (nicht eingezeichnet) in die Zukunft fortzuschreiben. Im Graph sind diese Schätzungen als blaue Punkte für die Tage 11 und 12 dargestellt.

Zeitreihenanalyse und AR-Modelle setzen voraus, dass Deine Verkäufe einem stationären oder vereinfacht gesagt, gleichmäßigen Verlauf folgen. Das heißt der Mittelwert und die Varianz Deiner Verkäufe müssen zu jeder Zeit gleich sein. In der Realität sind Verläufe aber nicht stationär, weshalb nicht-stationäre Verläufe vor ihrer Modellierung erst stationär gemacht werden müssen. In ARIMA-Modellen wird dies gemacht, weshalb ARIMA-Modelle weit verbreitet sind.