Nichtlineare Regression

Die lineare Regression ist nicht für alle Arten von Daten die beste Methode der Wahl, da Dein Datensatz auch andere Muster zeigen kann, als lediglich lineare Zusammenhänge. Die Nichtlineare Regression bietet Dir daher Modelle, um anders geartete Beziehungen zwischen UV und AV entsprechend abzubilden und anhand einer dennoch möglichst unkomplizierten mathematischen Funktion darzustellen.

Um eine nichtlineare Funktion zu schätzen kommen häufig sogenannte iterative Algorithmen zum Einsatz. Das sind Verfahren die versuchen eine Funktion zu finden, die möglichst gut zu Deinem Datensatz passt und sich diesem Ziel auf andere Weise annähern, als mit der Methode der kleinsten Quadrate, wie es bei der linearen Regression der Fall war.

Wie sieht ein nichtlineares Modell aus?

Ob eine Gleichung linear ist, erkennst Du daran, dass die unterschiedlichen Terme nur addiert werden (also z. B. ) und jeder der in der Funktion enthaltenen Terme mit nur einem Parameter multipliziert wird (bspw. wird x nur mit multipliziert). Nichtlineare Funktionen umfassen hingegen auch andere mathematische Operationen wie ln(x), , oder sin(x). Du siehst also, dass nichtlineare Gleichungen komplizierter aufgebaut sein können als lineare und es in der Regel schwierig ist sich anhand einer solchen Funktion vorzustellen, wie die Gleichung geplottet in einer Grafik aussieht.

Beispiel für eine nichtlineare Regression

Daher rufe Dir nun nochmal das Beispiel in Erinnerung, in dem wie die Auswirkungen von Koffeinkonsum auf die Konzentrationsfähigkeit untersucht haben. Im Kapitel der linearen Regression konnten wir bereits einen linearen Zusammenhang der beiden Variablen feststellen. Allerdings könnte es sein, dass eine zu hohe Koffeindosierung wieder zu einer Abnahme der Konzentrationsfähigkeit führt. Dazu erweitern wir unsere Stichprobe um 5 Personen und lassen diese zwischen 6 und 10 Tassen Kaffee trinken. In der unten abgebildeten Tabelle kannst Du Dir ansehen, welche Werte die 5 Personen bezüglich Konzentrationsfähigkeit erreicht haben.

	Person 1	Person 2	Person 3	Person 4	Person 5	Person 6
Koffeinkonsum (x)	3	0	5	2	1	4
Konzentrationsfähigkeit (y)	85	41	87	64	58	53
	Person 7	Person 8	Person 9	Person 10	Person 11
Koffeinkonsum (x)	8	10	7	9	6
Konzentrationsfähigkeit (y)	60	48	79	54	85

Da man sich den grafischen Zusammenhang der beiden Variablen kaum vorstellen kann, wenn man nur die Zahlenwerte sieht, plotten wir unseren Datensatz im nächsten Schritt und überprüfen so, ob die beiden Variablen immer noch einen linearen Zusammenhang aufweisen.

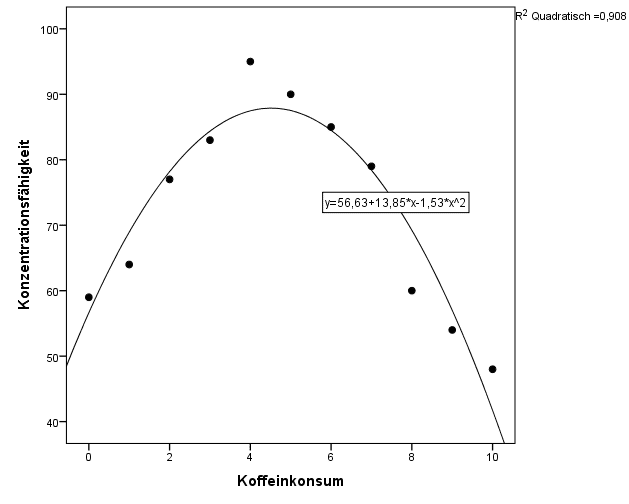
Offensichtlich lagen wir mit unserer Vermutung richtig und ein zu hoher Koffeinkonsum führt wieder zu einer Abnahme der Konzentrationsfähigkeit. Der ursprünglich lineare Zusammenhang war nur eine Täuschung, da wir die Beziehung der Variablen lediglich bis 5 Tassen Kaffee untersucht haben.

Quadratisches Modell

Eine Kurve wie bei unseren Daten ist eine sogenannte quadratische Funktion. Es kann äußerst aufwendig sein, die passende mathematische Gleichung zu finden, um Deinen Datensatz abzubilden. Quadratische Funktionen sind allerdings ähnlich unkompliziert wie lineare Funktionen, da Du sie im Plot leicht anhand ihrer Kurvenform erkennen kannst. Du erweiterst die ursprüngliche Regressionsgleichung einfach um den Term x². Die Gleichung sieht dann folgendermaßen aus:

   

Interpretieren kannst Du die nichtlineare Regression genauso wie die lineare Regression. Dabei steht  hauptsächlich das Gesamtmodell im Fokus steht und nicht mehr die einzelnen Regressionskoeffizienten. Der F-Test zeigt Dir, dass das Modell hochsignifikant ist . Gemäß dem Bestimmtheitsmaß werden durch die Variable Koffeinkonsum 90.8 % der Varianz von Konzentrationsfähigkeit aufgeklärt .