Logistische Regression

Die lineare und nichtlineare Regression konntest Du nur berechnen, wenn Deine abhängige Variable (AV) zumindest metrisch skaliert war. Möchtest Du aber eine diskrete AV untersuchen, ist die logistische Regression Deine Methode der Wahl. Weist Deine AV ein dichotomes Skalenniveau auf (bspw. „ja“ und „nein“ Antwortformat), wird die binäre logistische Regression angewandt, bei einer multinomialen Skala (mehr als zwei Antwortoptionen, bspw. „ja“, „nein“ und „vielleicht) kommt entsprechend die multinomiale logistische Regression zum Einsatz.

Mit Hilfe der logistischen Regression bist du dazu in der Lage Aussagen über die Wahrscheinlichkeit zu treffen, mit der eine bestimmte Ausprägung Deiner unabhängigen Variablen (UV) in einer Bedingung Deiner AV zu finden sein wird. Stell Dir wieder das Beispiel zum Thema Koffeinkonsum und Konzentrationsfähigkeit vor. Anstatt die Konzentration auf einer kontinuierlichen Skala von 1 bis 100 zu messen, könntest Du die Versuchspersonen einfach befragen, ob sie sich gerade konzentriert fühlen oder nicht. Damit hast Du ein dichotomes Antwortformat erzeugt.

Unterschied zur linearen Regression

Vielleicht fragst Du Dich jetzt, warum Du nicht trotzdem eine lineare Regression rechnen kannst? Sieh Dir dazu den unten abgebildeten fiktiven Datensatz an, in dem die Konzentrationsfähigkeit nun mit 1 (konzentriert) und 2 (unkonzentriert) kodiert ist.

	Person 1	Person 2	Person 3	Person 4	Person 5	Person 6
Koffeinkonsum (x)	3	0	5	2	1	4
Konzentrationsfähigkeit (y)	1	1	1	1	1	1
	Person 7	Person 8	Person 9	Person 10	Person 11
Koffeinkonsum (x)	8	10	7	9	6
Konzentrationsfähigkeit (y)	2	2	2	2	2

 

Damit Du dir den Zusammenhang der beiden Variablen besser vorstellen kannst, plotten wir sie wieder und legen zudem eine Regressionsgerade durch, damit klar ist, wieso die lineare Regression zur Analyse dichotomer AVs nicht geeignet ist

 

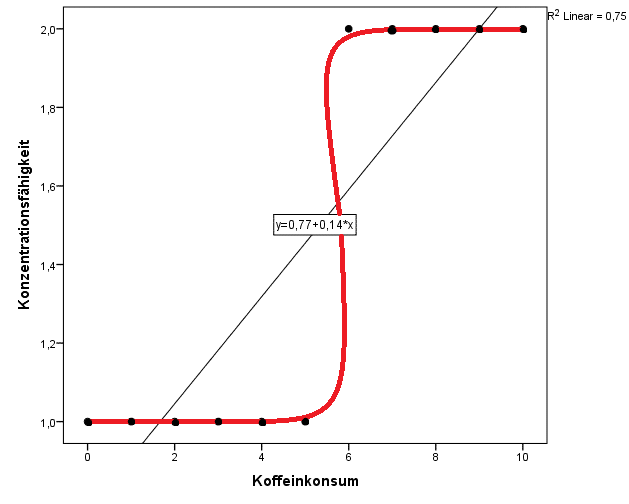
Wie Du siehst, lässt sich der Zusammenhang der beiden Variablen durch die Gerade nicht darstellen. Das Bestimmtheitsmaß der linearen Regression weißt zwar auf einen starken Effekt hin , was aber nur noch mehr verdeutlicht, wie wichtig es ist, Daten zu plotten, bevor man mit der eigentlichen statistischen Analyse beginnt. Ansonsten wäre man hier dazu verleitet, sich auf das Bestimmtheitsmaß zu verlassen. Und damit würde man eine völlig unpassende Methode anwenden, die nur durch Zufall ein gutes Ergebnis zeigt.

Die Regressionsgleichung würde sich bei zukünftigen Prognosen nicht nur auf die Zahlenwerte 1 und 2 beschränken (also konzentriert bzw. unkonzentriert). Stattdessen würde sie auch Zahlen berechnen, die im Rahmen unserer Variablenkodierung gar nicht existieren. Die rote Linie im Diagramm zeigt Dir, wie hingegen eine logistische Funktion in etwa aussieht. Sie wird hier auf unseren fiktiven Datensatz angewendet.

Wann ist ein logistisches Regressionsmodell signifikant?

Um zu überprüfen ob unser logistisches Regressionsmodell signifikant ist wird diesmal ein -Test durchgeführt, anstelle des F-Tests. Der -Test zeigt Dir, dass das Gesamtmodell auch mit diesem Untersuchungsdesign hoch signifikant ist .

Bei der logistischen Regression musst Du zur Beurteilung der Modellgüte ein anderes Bestimmtheitsmaß heranziehen, als das übliche . Es existieren mehrere Alternativen, von denen drei allerdings besonders bekannt sind, nämlich nach McFadden, Nagelkerke sowie Cox & Snell. Wie beim bisher besprochenen Bestimmtheitsmaß liegt der Wertebereich den r² annehmen kann auch bei diesen drei Varianten zwischen 0 und 1.

Unser Modell zeigt bspw. nach Cox & Snell eine sehr gute Modellgüte , was aber daran liegt, dass die Daten frei erfunden sind. In der Regel ist die Modellgüte bei realen Datensätzen schon als sehr gut zu bewerten, wenn das Bestimmtheitsmaß Werte von 0.3 erreicht.