Lineare Regression

Ziel der linearen Regression ist es, einen linearen Zusammenhang zwischen zwei Variablen zu modellieren. Das heißt Du möchtest eine abhängige Variable (AV) aus einer unabhängigen Variablen (UV) vorhersagen. Die mathematische Funktion, die diesem Verfahren zugrunde liegt, legt also eine Gerade zwischen die Datenpunkte und sieht in der Regel folgendermaßen aus:

   

Interpretation der Regressionskoeffizienten

Dabei sind β0 und β1 die sogenannten Regressionskoeffizienten des Modells. β0 wird auch Regressionskonstante genannt und gibt an, welchen Wert die AV (in diesem Fall y) hat, wenn die UV (hier durch x dargestellt) den Wert Null annimmt. Eine inhaltliche Interpretation dieses Koeffizienten macht nur dann Sinn, wenn die UV überhaupt den Wert Null annehmen kann. Würde man bspw. die Auswirkungen von Gewicht auf Bluthochdruck untersuchen, macht es wenig Sinn den Zahlenwert der Regressionskonstante inhaltlich zu interpretieren, wenn die UV gleich Null ist, da „kein Gewicht“ logischerweise auch nicht in Zusammenhang mit Bluthochdruck gebracht werden kann.

Der Regressionskoeffizient β1 wiederum spiegelt die Steigung der Regressionsgeraden wider und zeigt, wie stark sich die AV aufgrund der UV verändert. Das heißt, je größer der Zahlenwert von β1 ist, desto stärker ist der Einfluss der UV auf die AV ausgeprägt.

Modellannahmen

Damit Du die Ergebnisse der linearen Regression korrekt interpretieren kannst, müssen folgende Modellannahmen bzw. Voraussetzungen erfüllt sein:

• Die Variablen müssen zumindest grob linear zusammenhängen (sonst mach die gewählte mathematische Funktion keinen Sinn).
• Das Skalenniveau Deiner AV sollte zumindest metrisch sein, während die UV metrisch, aber auch dichotom-kategorial sein kann.
• Die Residuen sollten keine Korrelation untereinander aufweisen und näherungsweise normalverteilt sein.
• Zudem sollten die Residuen konstant über den gesamten Wertebereich der AV streuen (= Homoskedastizität).

Beispiel einer linearen Regression

Erinnere Dich nun nochmal an das Beispiel aus dem Kapitel der Varianzanalyse, bei dem wir untersuchen wollten, inwiefern sich Koffeinkonsum auf die Konzentrationsfähigkeit auswirkt. Um das Studiendesign besser an das Verfahren der linearen Regression anzupassen bilden wir diesmal keine Gruppen, sondern messen genau, wie viel Koffein die Versuchspersonen konsumieren. Zur Vereinfachung bzw. Veranschaulichung operationalisieren wir die UV insofern, dass  die Probanden 0 bis 5 Tassen Kaffee trinken. Die Methode zur Messung der Konzentrationsfähigkeit behalten wir bei. Stell Dir vor, Du hast 6 Leute im Rahmen Deiner Studie untersucht und bist zu folgenden Ergebnissen gekommen:

	Person 1	Person 2	Person 3	Person 4	Person 5	Person 6
Koffeinkonsum (x)	3	0	5	2	1	4
Konzentrationsfähigkeit (y)	83	59	90	77	64	95

Bevor wir uns die statistischen Resultate der linearen Regression ansehen, ist es äußerst wichtig, vorher anhand eines Diagramms zu überprüfen, wie der Datenzusammenhang aussieht und ob eine lineare Funktion dem Datenmuster überhaupt gerecht wird. Wenn Du die Daten plottest und eine Regressionsgerade durchlegst, ergibt sich das nachfolgende Bild:

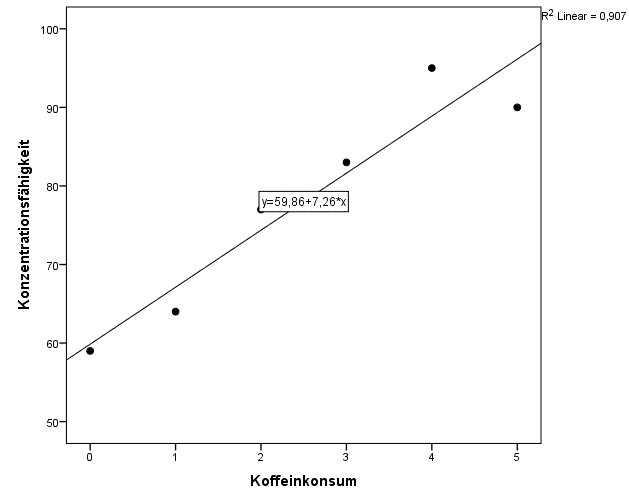
Wie Du siehst, beschreibt die Regressionsgerade die Datenstruktur sehr gut. Dem Diagramm kannst Du auch die berechneten Werte der Regressionskoeffizienten entnehmen, d. h. und . Anhand dieser Koeffizienten kannst Du Prognosen darüber treffen, wie gut sich Personen konzentrieren können, wenn Du das Ausmaß ihres Koffeinkonsums kennst.

Das Bestimmtheitsmaß zeigt Dir, dass der Effekt von Koffeinkonsum auf Konzentrationsfähigkeit sehr stark ist, da Du Durch die UV 90.7 % der Varianz der Variable Konzentrationsfähigkeit aufklären kannst. Der Output Deiner Statistiksoftware sollte Dir zudem zeigen, dass der F-Test eine hohe Signifikanz des Modells anzeigt . Du siehst also, dass man dieselben Fragestellungen sowohl mit varianzanalytischen, als auch mit Hilfe von Regressionsmodellen untersuchen kann.