Regressionsanalysen

Regressionsanalysen sind statistische Verfahren, mit denen Du berechnen kannst, ob eine oder mehrere unabhängige Variable (UV) eine abhängige Variable (AV) beeinflussen. Dabei berechnest Du auch wie stark der Zusammenhang zwischen diesen Variablen ist. Im Gegensatz zu einer Korrelation ist es Dir somit möglich, gerichtete bzw. kausale Effekte zu untersuchen und nicht nur bloße Zusammenhänge zu ermitteln. Die UV wird im Rahmen von Regressionsanalysen auch als Prädiktor, Ursache oder Regressor bezeichnet. Die AV nennt man auch Zielvariable, Wirkung oder Regressand.

Idee der Regressionsanalyse

Es gibt verschiedene Formen der Regressionsanalyse, die sich unter anderem hinsichtlich der Verfahren zur Abschätzung der Variablenbeziehung unterscheiden. Eines der am häufigsten angewandten Verfahren zur Modellierung solcher Effekte ist das der kleinsten Quadrate. Dabei wird versucht, die Summe der Abstände aller erhobenen Datenpunkte hinsichtlich einer Bezugslinie zu minimieren. Willst Du beispielsweise eine lineare Funktion durch Deine Datenpunkte legen, weil Du der Meinung bist, dass deren Zusammenhang dadurch am besten dargestellt wird, könnte die Modellierung grafisch folgendermaßen aussehen.

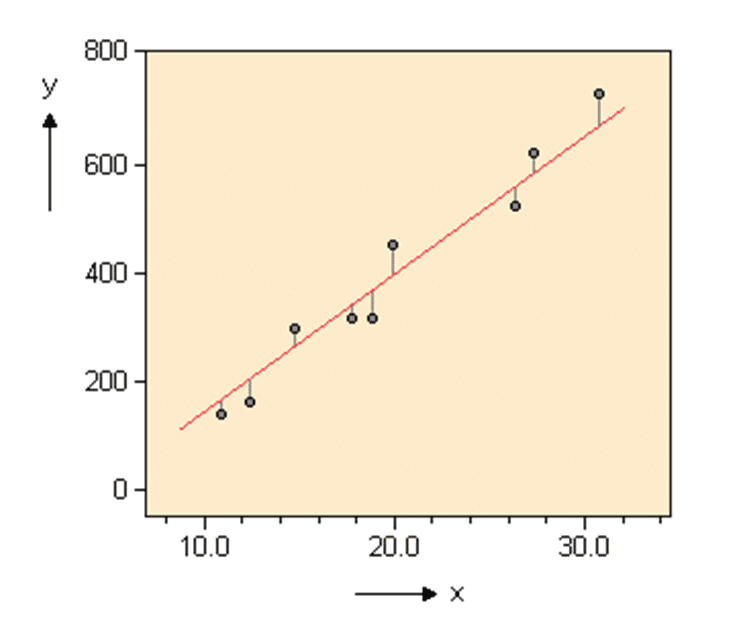
Bei Regressionsanalysen wird generell immer eine mathematische Funktion gesucht, die das vorliegende Datenmuster zwar gut beschreibt, gleichzeitig aber nicht zu komplex ist. Diese Funktion kann die Beziehung Deiner Variablen dann allerdings nicht exakt widergeben, sondern sich den wahren Zusammenhängen nur annähern. Sie führt immer einen Fehlerterm mit sich. Dieser Fehlerterm wird grafisch durch die Abweichung der Datenpunkte von der berechneten Funktion dargestellt, welche als Residuen bezeichnet werden. Residuen sind demnach Zufallskomponenten Deines Regressionsmodells, die nicht durch Beobachtung erklärt werden.

Wie schließt man auf Signifikanz?

Hast Du eine Regressionsfunktion berechnet, bedeutet das jedoch nicht, dass sie auch signifikant ist. Du kannst also nicht automatisch mit dem ermittelten Muster auch Aussagen über eine Grundgesamtheit treffen oder zukünftige Ausprägungen der AV vorhersagen. Deine Regressionsfunktion mag zwar statistisch korrekt berechnet sein, es ist jedoch möglich, dass Du z. B. wichtige UVs in der Planungsphase nicht berücksichtigt hast. Das führt unter Umständen dazu, dass das reale Phänomen nicht vollständig widergespiegelt wird.

Inwiefern sich das Regressionsmodell auf die zugrundliegende Population übertragen lässt, kannst Du wie bei der Varianzanalyse mit der F-Statistik testen. Für jede berechnete Regressionsfunktion werden auch entsprechende statistische Kenngrößen, so genannte Regressionskoeffizienten ausgegeben. Die Signifikanz dieser Koeffizient erfasst man mittels t-Test.

Die Modellgüte

Zur Überprüfung der Güte Deines Regressionsmodells werden vor allem der Korrelationskoeffizient r und das Bestimmtheitsmaß herangezogen. Der Korrelationskoeffizient gibt Auskunft über Größe und Richtung des Zusammenhangs zweier Variablen. Je näher r an +1 oder -1 liegt, desto stärker hängen zwei Variablen positiv oder negativ zusammen.

Da Du bei einer Regressionsanalyse von einem kausalen Zusammenhang ausgehst, bedeutet ein signifikantes r, dass sich die AV quantitativ verändert, wenn sich die UV um eine Einheit ändert. Im Gegensatz dazu gibt das Bestimmtheitsmaß an, wie viel Prozent der Varianz der AV Du durch die UVs erklären kannst. Der Zahlenwert liegt daher immer zwischen 0 % und 100 %. Das Bestimmtheitsmaß steigert sich allerdings nicht nur durch vermehrte Varianzaufklärung, sondern auch durch die Anzahl der Prädiktoren die in das Modell einfließen. Bei der Interpretation von ist daher mit Bedacht vorzugehen.

Gängige Regressionsanalysen umfassen :

• Lineare Regression
• Multiple (lineare) Regression
• Logistische Regression
• Multinomiale logistische Regression
• Multivariate Regression