Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Random Effects-Modell
Random Effects-Modell
Keine Kommentare
Im Gegensatz zu Fixed Effects-Modellen betrachtet das Random Effects-Modell individuelle, unbeobachtete Effekte als zufällig Effekte. Im Fixed Effects-Modell nehmen wir unbeobachtete, individuelle Effekte als über die Zeit konstante oder fixe Effekte an. In einem Random Effects-Modell betrachtest Du diese nun als Zufallsvariablen. Deshalb werden Random Effects-Modelle auch als Mixed Effects-Modelle bezeichnet. Es werden sowohl Effekte von Variablen geschätzt, die zwischen den Individuen variieren, als auch von Variablen, die innerhalb der Individuen variieren. Fixed Effects-Modelle konzentrieren sich dagegen nur auf die Varianz innerhalb der Individuen („within“-Schätzung).
Wann kann man ein Random Effects-Modell anwenden?
Das hat vor allem zur Folge, dass die erklärenden Variablen von der unbeobachteten Heterogenität unabhängig sein müssen. Willst Du zum Beispiel den Einfluss des Lebensstils und von Konsumgewohnheiten auf Kaufentscheidungen analysieren, setzt das Random Effects-Modell voraus, dass Du sowohl Lebensstil als auch Konsumgewohnheiten kontrollierst. Fehlen Dir aber bspw. Informationen zu Gewohnheiten der Konsumenten, wirst Du verzerrte Ergebnisse erhalten, da der Lebensstil sehr wahrscheinlich auch von den individuenspezifischen, aber nun unbeobachteten Gewohnheiten abhängt. Du musst also alle relevanten Drittvariablen explizit kontrollieren, um unverzerrte Ergebnisse zu erhalten.
Der große Vorteil in der Betrachtung individuenspezifischer Effekte als zufällige Effekte ist dann aber, dass individuelle Charakteristika wie Lebensstil oder Konsumgewohnheiten, die über die Zeit konstant sind, auch explizit modelliert werden können. In einem Fixed Effects-Modell ist dies nicht möglich, da hier die individuelle Heterogenität ja als konstant angenommen wird.
Abgrenzung zu anderen Modellen
In einfacheren gepoolten Querschnittsmodellen wird die Paneldatenstruktur noch nicht berücksichtigt und damit auch kein dynamischer Einfluss der Zeit auf die individuellen Effekte. Das Random Effects-Modell als Paneldatenanalyse geht genau hier einen Schritt weiter. Die unbeobachtete Heterogenität soll zwar insgesamt unabhängig von den erklärenden Variablen sein, aber darf von sich selber abhängen. Die Zeit, das heißt vergangene Beobachtungen spielen für die individuelle, unbeobachtete Heterogenität wie Konsumgewohnheiten nun eine Rolle und können auf diese Einfluss nehmen – sie ist seriell korreliert. Einfache, gepoolte OLS-Schätzungen berücksichtigen noch keine serielle Korrelation (oder auch Autokorrelation), weshalb das Random Effects-Modell auf andere Schätzverfahren zurückgreifen muss, um die Panelstruktur (und damit serielle Korrelation) der Daten zu berücksichtigen. In der Regel wird dafür auf die „feasible“ generalisierte kleinste Quadrate-Schätzung (kurz FGLS-Schätzung) zurückgegriffen. Das Random Effects-Modell kannst Du Dir dann als Mixed Effects-Modell folgendermaßen vorstellen:
![\[\left(y_{it}-\lambda\overline{y_i}\right)=\left(X_{it}-\lambda \overline{X_i}\right)+\left({\varepsilon}_{it}-\overline{{\varepsilon}_i}\right)+\ (1-\lambda)u\ \]](https://www.statistik-nachhilfe.de/wp-content/ql-cache/quicklatex.com-77ad284a2a08f9f0d968a6f215431209_l3.png "Rendered by QuickLaTeX.com")
Im Artikel über Fixed Effects findest Du ein sehr ähnliches Modell und auch ein Analyse-Beispiel. Im Vergleich zu Fixed Effects-Modellen machst Du dir in einem Random Effects-Modell aber nun Informationen über individuelle, unbeobachtete Heterogenität zunutze. Du möchtest die Unterschiede zwischen und innerhalb der Individuen (deshalb Mixed Effects) gemäß ihrem Gewicht
in die Schätzung mit einbeziehen. Dies ist der einzige Unterschied und gleichzeitig einzige Zusatz zum Fixed Effects-Modell. Random Effects-Modelle sind also vereinfacht eine Mischung aus Pooled OLS und Fixed Effects-Modell: Bei =1
liegt das Gewicht auf den Unterschieden innerhalb der Individuen und das Mixed Effects-Modell wird zum Fixed Effects-Modell – die individuelle, unbeobachtete Heterogenität 
löst sich auf. Bei 
liegt das Gewicht auf Unterschieden zwischen den Individuen und das Random Effects-Modell wird zum Pooled OLS-Modell. Das Gewicht ist mit 
Zeitpunkten und den Standardfehlern der Residuen 
und 
definiert als:
![\[\lambda\mathrm{=}1-\frac{{\sigma}_{\varepsilon}}{\sqrt{{{\sigma }_{\varepsilon}}^2+T{{\sigma}_u}^2}}\]](https://www.statistik-nachhilfe.de/wp-content/ql-cache/quicklatex.com-e436c754d9d6b95d75138ee09c1d4d83_l3.png "Rendered by QuickLaTeX.com")
Beispiel für ein Random Effects-Modell
Angenommen, wir wollen den Einfluss des Einkommens auf den Stromverbrauch mit folgenden Daten schätzen:
Haushalt ( ) |
Jahr ( ) |
Einkommen (€) | Stromverbrauch (kWh) |
| A | 2015 | 1000 | 4000 |
| A | 2016 | 1200 | 4100 |
| A | 2017 | 1500 | 42000 |
| B | 2015 | 2000 | 3000 |
| B | 2016 | 2200 | 3100 |
| B | 2017 | 2500 | 3200 |
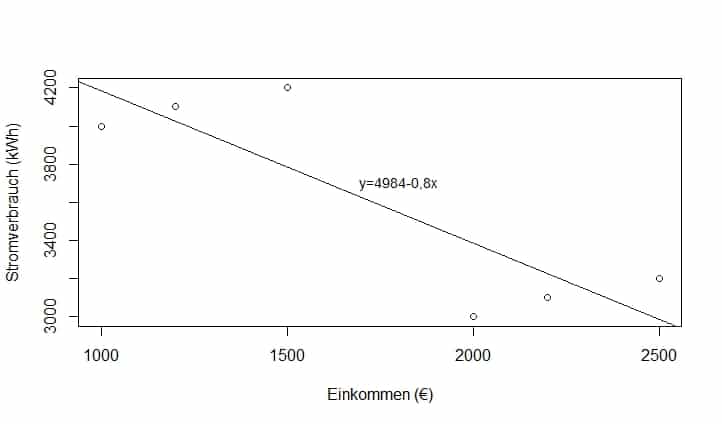
Die Standardfehler der Residuen kannst Du über ein Fixed Effects-Modell schätzen. Mit einem geschätzten 
liegt das Gewicht auf den Unterschieden zwischen den Individuen. Das Random Effects-Modell ist in diesem Falle nahe einer Pooled OLS-Schätzung mit einem negativen Einfluss des Einkommens auf den Stromverbrauch, wie auch untenstehende Graphik zeigt (-0,8). Mit einem Hausman-Test kannst Du überprüfen, ob das Fixed Effects- oder das Random Effects-Modell bessere Ergebnisse erzielt. Liegen große Unterschiede in den geschätzten Koeffizienten wie in unserem Falle vor (negativ im Falle von Random Effects, positiv im Falle von Fixed Effects), liefert nur das Fixed Effects-Modell bessere, konsistente Ergebnisse. Das Random Effects-Modell ist also ungeeignet, um den tatsächlichen Einfluss des Einkommens der Haushalte auf den Stromverbrauch zu schätzen:
Zusammenfassung
Fixed Effects-Modelle betrachten die individuelle, unbeobachtete Heterogenität als fix und können deshalb diese nicht explizit schätzen. Gepoolte Querschnittsmodelle berücksichtigen keine Panelstruktur in Daten und betrachten Unterschiede innerhalb der Individuen als ob diese von unterschiedlichen Individuen stammen. Eine Pooled OLS-Schätzung würde deshalb allen Informationen, also sowohl den Unterschieden zwischen als auch innerhalb der Individuen gleiches Gewicht geben. Wenn es tatsächlich der Fall ist, dass die erklärenden Variablen und die unbeobachtete, individuelle Heterogenität voneinander unabhängig sind, dann ist das Random Effects-Modell effizienter als das Fixed Effects-Modell. Denn dann kann individuelle Heterogenität nicht einfach als „fix“ betrachtet und eliminiert werden. Random Effects-Modelle sind dann auch genauer als gepoolte Schätzungen. Schließlich können sie Unterschiede innerhalb der Individuen und den Einfluss der Zeit auf selbige berücksichtigen.