Pooled Cross Sections

Die Analyse von Pooled Cross Sections ist die einfachste Form einer Paneldatenanalyse, da es eigentlich kein Panelmodell ist. Wie der Name schon sagt, handelt es sich um gepoolte oder zusammengefasste Querschnittsdaten. Querschnittsdaten können dann zusammengefasst werden, wenn von verschiedenen Individuen zu verschiedenen Zeitpunkten dieselben Informationen vorliegen. In erster Linie ermöglichen Dir gepoolte Daten ein größeres Sample. Ein größeres Sample verspricht wiederum bessere und genauere Schätzungen. Aber auch Veränderungen kannst Du mithilfe gepoolter Querschnittsdaten analysieren. Stell Dir vor, Du hast Informationen über die Anzahl von Onlinekäufen von 3 Personen in den Jahren 1995, 2005 und 2015 sowie das Alter der Personen:

Jahr	Anzahl Onlinekäufe	Alter
1995	10	20
1995	5	40
1995	1	60
2005	20	20
2005	15	40
2005	10	60
2015	30	20
2015	40	40
2015	35	60

Was könnte die Forschungsfrage sein?

Es interessiert Dich nun, ob die Anzahl der Onlinekäufe vom Alter abhängt und ob sich diese über die Zeit verändert hat. Den Einfluss des Alters auf die Zahl der Onlinekäufe kannst Du mithilfe einer einfachen linearen Regression und der Methode der kleinsten Quadrate schätzen. Deshalb werden gepoolte Modelle in der Regel als Pooled OLS (Ordinary Least Squares) bezeichnet.

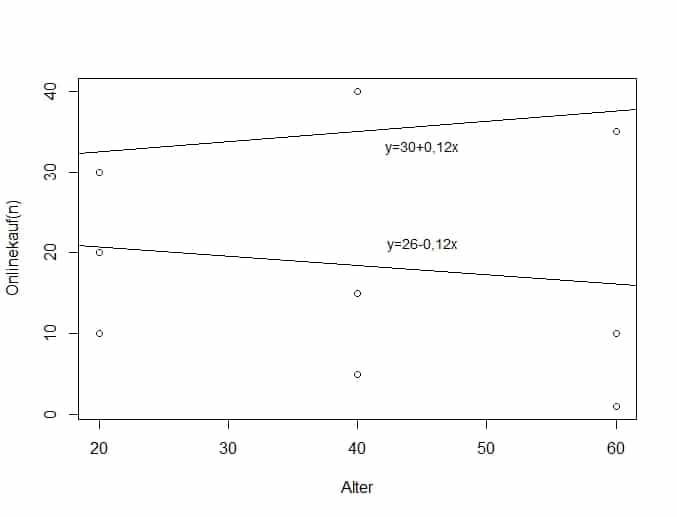
Der untenstehende Graph zeigt die Zahl der Onlinekäufe zum jeweiligen Alter in den Jahren und die entsprechende Regressionsgerade. Die untere Linie zeigt, dass die Zahl der Onlinekäufe mit steigendem Alter abnimmt (-0,12). Unabhängig vom Jahr der Onlinekäufe siehst Du hier also einen negativen Zusammenhang zwischen Onlinekauf und Alter. Der Scatterplot lässt uns aber vermuten, dass es Unterschiede und Veränderungen zwischen den beobachteten Jahren gibt.

Ein Blick in die Tabelle mit den Daten lässt vermuten, dass sich vor allem im Jahr 2015 gegenüber 2005 und 1995 Veränderungen ergeben haben. Onlinekäufe scheinen im Jahr 2015 nicht mehr mit dem Alter zusammenhängen. Die Onlinekäufe könnten nun sogar mit dem Alter zunehmen. Die positive Steigung der oberen Regressionsgerade für die Onlinekäufe im Jahre 2015 bestätigt den Eindruck. 2015 siehst Du einen positiven Zusammenhang zwischen Alter und der Zahl der Onlinekäufe (+0,12). Wenn Du also die Zeitdimension in Deiner Analyse berücksichtigst, wirst Du bessere und differenziertere Ergebnisse erzielen können, als eine einfache Analyse ohne Berücksichtigung der Zeit.

Wie sieht das Modell aus?

Um in gepoolten Modellen den Einfluss der Zeit abbilden zu können, nimmst Du die entsprechenden Jahre als Dummy-Variablen in dein Modell auf. Der Effekt gibt dann die durchschnittliche Veränderung im jeweiligen Jahr wieder. Darüber hinaus kannst Du noch die Veränderungen des Einflusses wichtiger Variablen wie die des Alters in den Jahren schätzen (), indem Du Interaktionsterme zwischen den Jahresdummys und relevanter Variablen bildest (). Im einfachsten Falle sieht Dein Regressionsmodell dann so aus:

   

Wenn du dieses Modell mit den obigen Daten als Pooled OLS schätzt, wirst Du feststellen, dass im Jahr 2015 () im Schnitt 20 Onlinekäufe mehr getätigt werden und mit zunehmendem Alter auch die Onlinekäufe zunehmen (um 0,36 pro Altersjahr) und eben nicht abnehmen, wie es das einfache Regressionsmodell nahegelegt hätte.

Allerdings ist das gepoolte Modell ungeeignet für die Analyse von richtigen Paneldaten. Panelmodelle sind dafür besser geeignet. Das sind z. B. Fixed Effects-Modelle oder Random Effects-Modelle. Sie nutzen die Information derselben Individuen über die Zeit besser aus. In gepoolten Modellen werden Paneldaten als Querschnittsdaten betrachtet. Beobachtungen für die gleichen Individuen über die Zeit gelten als Beobachtungen für unterschiedliche Individuen. Damit können wichtige Dynamiken und Einflüsse wie serielle Korrelation der Beobachtungen innerhalb von Individuen nicht berücksichtigt werden. Sie verzerren die Schätzung.