Fixed Effects-Modell

Fixed Effects-Modell

  • 5. Februar 2018
  • Posted by: Mika
Keine Kommentare

In einem Fixed Effects-Modell nehmen wir an, dass unbeobachtete, individuelle Charakteristika wie Geschlecht, Intelligenz oder Präferenzen konstant oder eben „fix“ sind. Stell Dir beispielsweise vor, Du willst herausfinden, welcher Zusammenhang zwischen dem monatlichen Einkommen eines Haushalts und dessen Stromverbrauch pro Jahr besteht. Um den Zusammenhang zu testen, liegen Dir Daten von zwei fiktiven Haushalten A und B mit einem Einkommen und Stromverbrauch zu drei Jahren vor.

Haushalt (i) Jahr (t) Einkommen (€) Stromverbrauch (kWh)
A 2015 1000 4000
A 2016 1200 4100
A 2017 1500 4200
B 2015 2000 3000
B 2016 2200 3100
B 2017 2500 3200

Den Zusammenhang zwischen Einkommen und Stromverbrauch eines Haushalts kannst Du mithilfe einer linearen Regression analysieren. Zur Analyse hast Du nun prinzipiell zwei Möglichkeiten – die Analyse der Daten als Querschnittsdaten oder eben als Paneldaten. Für den ersten Fall nehmen wir an, Du kannst Einkommen und Stromverbrauch keinem Haushalt zuordnen. Dann würdest Du alle Stromverbräuche auf alle Einkommen über alle Jahre regressieren. Als Ergebnis würdest Du dann die Regressionsgerade A/B im Scatterplot unten sehen. Hier sinkt der Stromverbrauch der Haushalte mit steigendem Einkommen. Ordnest Du aber Stromverbrauch und Einkommen den Haushalten zu und regressierst dann den Stromverbrauch auf das Einkommen innerhalb der einzelnen Haushalte, ergibt sich ein umgedrehtes Bild. Wie Du anhand den Regressionsgeraden A und B sehen kannst, steigt hier der Stromverbrauch bei steigendem Einkommen.

Fixed Effects Modell

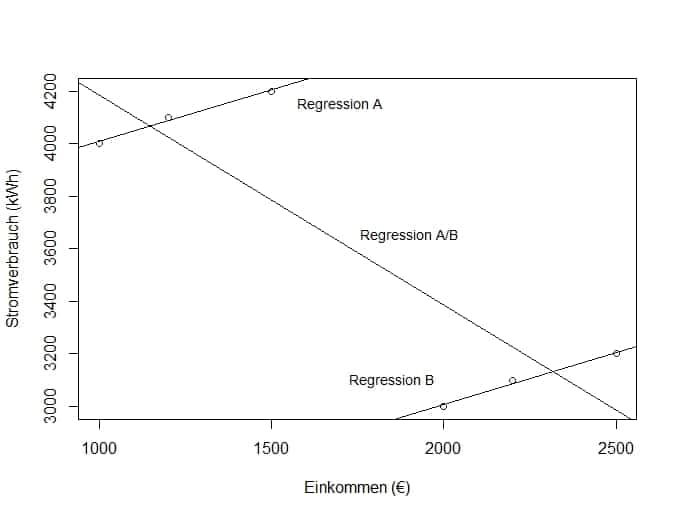
Wenn Du innerhalb der Haushalte den Effekt des Einkommens auf den Stromverbrauch analysierst, wirst du richtigerweise einen steigenden Effekt feststellen.

Wie sieht das Modell aus?

Entscheidend ist, dass die Panelregressionen die unbeobachtete, individuelle Heterogenität in zwei Fehlerterme aufteilt. Ein Fehlerterm sammelt alle unbeobachteten Variablen, die sich innerhalb der Individuen über die Zeit verändern (\varepsilon_{it}). Ein anderer Fehlerterm sammelt alle Variablen, die sich innerhalb der Individuen nicht ändern (\mu _i). Fixed Effects-Modelle nehmen an, dass die individuelle, unbeobachtete Heterogenität (\mu_i) über die Zeit konstant, unverändert und „fix“ ist. Dein Panelmodell mit Stromverbrauch y und Einkommen X sieht dann im einfachsten Falle so aus:

    \[y_{it}=X_{it}+{\varepsilon}_{it}+{\mu}_i\]

Wichtig und vorteilhaft ist dabei, dass in einem Fixed Effects-Modell die individuelle, unbeobachtete Heterogenität von den erklärenden Variablen abhängig sein kann. In einem Fixed Effects-Modell nimmst Du also an, dass die erklärenden Variablen mit der individuellen, unbeobachteten Heterogenität korrelieren. Mithilfe eines Hausman-Tests kannst Du dies überprüfen. Oft ist es der Fall, dass die erklärenden Variablen und unbeobachtete Heterogenität korrelieren. Dann ist ein Fixed Effects-Modell die statistisch bessere Wahl gegenüber einem Modell mit zufälligen Effekten ist.

Welche Möglichkeiten gibt es das Modell zu schätzen?

Es bestehen dann zwei Möglichkeiten, wie Du ein Fixed Effects-Modell schätzen kannst. Zum einen kannst Du für jedes Individuum eine Dummy-Variable modellieren, die die individuellen, fixen Charakteristika von (im Sinne von „i-sein“) repräsentiert. Das Modell kannst Du dann mithilfe von least squares dummy variables (kurz LSDV-Modell) schätzen. Die Schätzung von individuellen Dummy-Variablen wird aber bei größeren Stichproben schnell problematisch und unpraktisch, weshalb die within-Transformation gern Anwendung findet. Dabei werden die Mittelwerte von y_{it} und X_i bzw. \varepsilon_i und {\mu_i gebildet und jeweils von y_{it}, X_{it} bzw. \varepsilon_{it} und {\mu}_i subtrahiert. Dadurch wird die individuelle, unbeobachtete Heterogenität {\mu}_i „rausgemittelt“ (\mu_i-\overline{\mu}_i=0, da diese konstant ist) und verschwindet im Fixed Effects-Modell:

    \[(y_{it}-\overline{y_i})=(X_{it}-\overline{X_i})+({\varepsilon}_{it}-\overline{{\varepsilon}_i})\]

Vor- und Nachteile der Schätzer

Der LSDV-Schätzer als auch die within-Schätzung liefern identische Schätzergebnisse. Allein deren Herangehensweise ist eine andere. Wie der Name schon sagt, werden individuelle Charakteristika im LSDV-Schätzer über Dummy-Variablen kontrolliert. Bei der within-Transformation werden diese einfach rausgemittelt. Dadurch maximierst Du die Varianzaufklärung innerhalb der Individuen.

Geschätzt werden also Unterschiede innerhalb der Individuen, Unterschiede zwischen den Individuen spielen allerdings keine Rolle mehr. Ein Fixed Effects-Modell nimmt letztlich an, dass konstante, zeitinvariante oder „fixe“ Eigenschaften der Individuen keine Gründe für Veränderungen darstellen können und kontrolliert diese. Auch wenn Du solche „fixen“ Effekte wie Geschlecht, oft aber auch andere latente Eigenschaften wie Intelligenz oder Präferenzen, nicht direkt messen kannst, kannst Du diese trotzdem in einem Fixed Effects-Modell kontrollieren.

Der Nachteil ist allerdings, dass Du jene konstanten oder „fixen“ Variablen nicht mehr direkt als erklärende Variablen in Dein Modell aufnehmen kannst. Wenn Du aber gerade den Einfluss von latenten Eigenschaften einer Person auch direkt schätzen willst, landest Du häufig in einer Zwickmühle. Dann kann die Wahl eines Modells mit zufälligen statt fixen Effekten für Dich theoretisch sinnvoller sein.