Multidimensionale Skalierung

Multidimensionale Skalierung

  • 26. April 2018
  • Posted by: Mika
Keine Kommentare

Menschen beurteilen die meisten „Objekte“ bewusst oder unbewusst anhand von Kriterien. In welchem Maße einzelne Objekte diese Kriterien erfüllen, bestimmt dann ihre Lage im Wahrnehmungsraum und es lassen sich Distanzen zwischen je zwei Objekten bestimmen.

Stell Dir vor, Lehrer einer Klasse werden anhand der beiden Kriterien Freundlichkeit und Kompetenz bewertet:

i Name Kompetenz Freundlichkeit
1 Herr Müller (8;2) 8 2
2 Herr Schulz (2;4) 2 4
3 Herr Soberlein (6;9) 7 5

Trägst Du diese Bewertungen in ein Koordinatensystem ein, so ergibt sich die folgende Anordnung im Wahrnehmungsraum:

Multidimensionale Skalierung

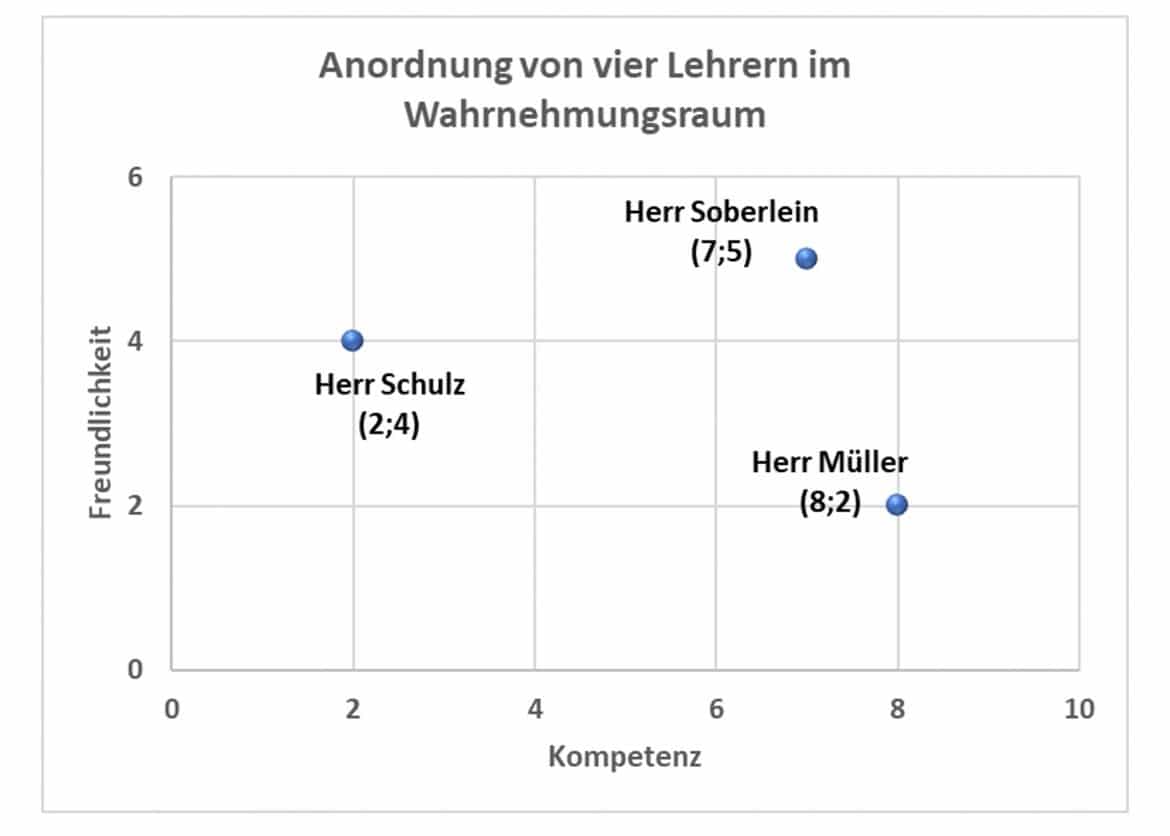
Misst Du die Abstände im Koordinatensystem zwischen je zwei Lehrern, so erhältst Du Angaben in Zentimetern, die Du als Maß für ihre Unähnlichkeit interpretieren kannst.

Die Verfahren der Muldimensionalen Skalierung (MDS) gehen genau den umgekehrten Weg. Sie schließen aus globalen Unähnlichkeitsaussagen bezüglich einer Reihe von Objekten auf deren Lage im Wahrnehmungsraum, die Konfiguration. Dabei wird die Anordnung so gewählt,

  • dass die Unähnlichkeitsaussagen den Distanzen der Objekte entsprechen: je unähnlicher zwei Objekte sind, umso weiter sollten sie voneinander entfernt liegen und
  • dass die dazu benötigte Anzahl von Dimensionen möglichst gering ist: Die Dimensionen werden später als die Beurteilung beeinflussende Eigenschaften interpretiert.

Die verschiedenen Verfahren der MDS unterscheiden sich zum einen im Skalenniveau der Ausgangsdaten; hier stehen die älteren metrischen Verfahren den jüngeren nicht-metrischen Verfahren gegenüber, die mit – leichter erhebbaren-ordinalskaliertem – Material auskommen.

Zum anderen kannst du aggregierende Verfahren (einfache MDS), die von je einem Urteil pro Objektpaar ausgehen, von individuellen Verfahren (wiederholte MDS) unterscheiden, die interpersonelle Unterschiede in der Wahrnehmung berücksichtigen. Einige dieser Verfahren (INDSCAL) berücksichtigen noch unterschiedliche Gewichtungen der Kriterien bei verschiedenen Personen.

Im einfachsten Fall führst Du ein metrisch-aggregierendes Verfahren durch. Du benötigst dann metrisch skalierte Unähnlichkeitsmaße \delta_{ij}, für i,j=1,..n zwischen n Objekten, für die gilt:

  • \delta_{ii}=0, für alle i
  • \delta_{ij} > 0, für alle i \ne j
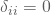  • \delta_{ij} = \delta_{ji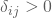}, für alle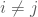 i,j
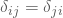  • \delta_{ij} + \delta_{jk} \ge \delta_{ik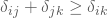} für alle i,j,k

Alle Unähnlichkeitsmaße zusammen ergeben die Matrix \Delta:

    \begin{equation*} \Delta=\left[ \begin{array} \ \delta_{11}...\delta_{1n}\\ ..\quad\quad.. \\\delta_{n1}...\delta_{nn} \end{array} \right]\end{equation*}

Durch Quadrieren der Werte, deren doppelte Zentrierung und Multiplikation mit -\frac 1 2 erhältst Du daraus eine Matrix B= (b_{ij}), mit

    \begin{equation*} b_{ij}= -\frac 1 2 \cdot ( \delta_{ij}^2 - \delta_{i\cdot}^2-\delta_{\cdot j}^2+\delta_{\cdot\cdot}^2) \end{equation*}

wobei

    \begin{equation*} \delta_{i\cdot}^2 = \frac 1 n \cdot \sum_{j=1}^n \delta_{ij}^2, \quad \delta_{\cdot j}^2 = \frac 1 n \cdot \sum_{i=1}^n \delta_{ij}^2 \quad und \quad \delta_{\cdot\cdot}^2 = \frac 1 {n^2} \cdot \sum_{i=1}^n\sum_{j=1}^n \delta_{ij}^2 \end{equation*}

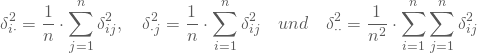
Aus dieser Matrix B berechnest Du mittels Eigenwertzerlegung die Eigenwerte \lambda_k und die zu den m-größten Eigenwerten zugehörigen Eigenvektoren \vec e_k von B. Dann erhältst Du die gesuchten Koordinaten X im m-dimensionalen Raum als:

    \begin{equation*} X_{(nxm)} = \Lambda_{(nxm)} \cdot E_{(mxm)}^{\frac 1 2} \end{equation*}

wobei

  • X die Matrix der gesuchten Koordinaten von n Objekten im m-dimensionalen Raum darstellt,
  • \Delta die Matrix der zu den m größten Eigenwerten gehörigen Eigenvektoren und
  • E die Diagonalmatrix der m größten Eigenwerte darstellt.

Für Dein Beispiel erhältst Du auf diese Weise die folgende Darstellung im zweidimensionalen Raum:

Darstellung im zweidimensionalen Raum

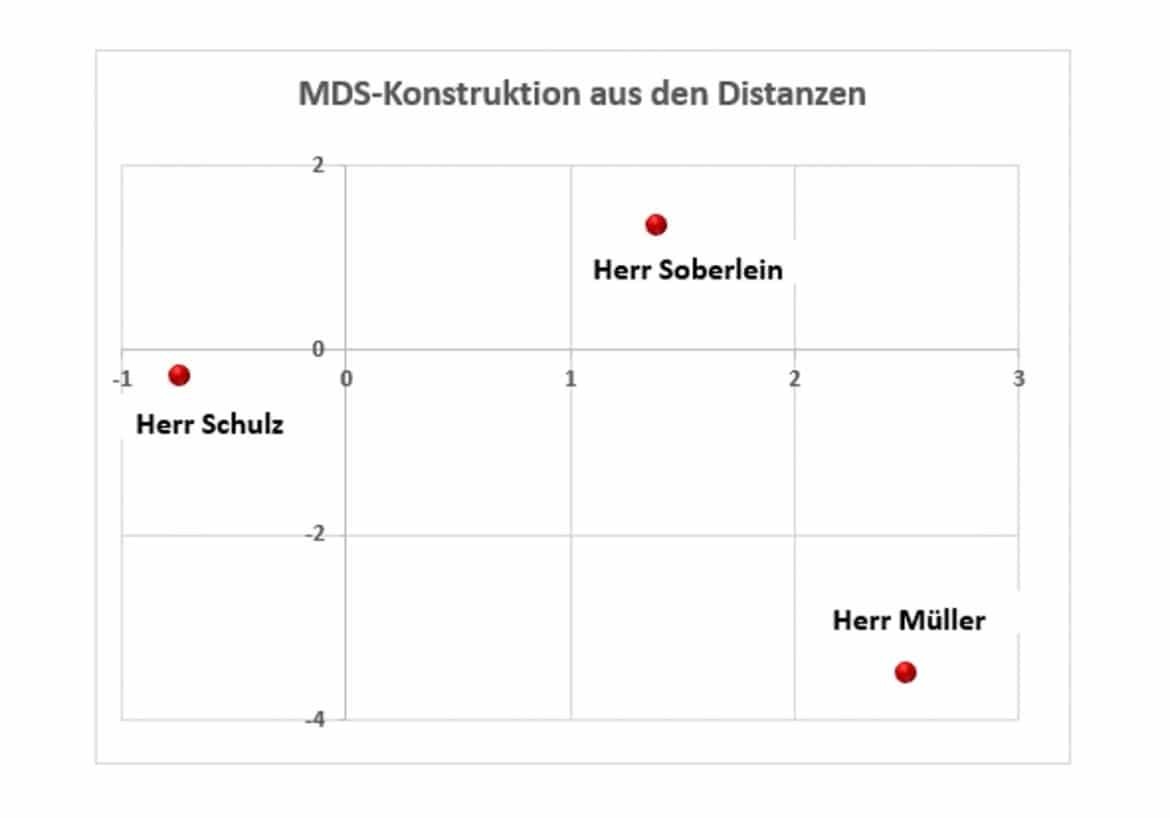
Immer lassen sich die Distanzen von n Objekten im (n-1)-dimensionalen Raum darstellen. Du kannst beispielsweise im zweidimensionalen Raum ein eindeutiges Dreieck konstruieren, wenn Du die Abstände zwischen den drei Eckpunkten kennst. Gilt m<(n-1), so stimmen die Distanzen Deiner Konfiguration in der Regel nicht exakt mit den ursprünglichen Unähnlichkeitsmaßen überein.

Der Stress Deiner Konfiguration ist ein Maß für die Güte der Übereinstimmung zwischen den Unähnlichkeitsmaßen \delta_{ij} und und den Distanzen d_{ij} und ergibt sich als normierte Quadratsumme dieser Abweichungen:

    \begin{equation*} Stress = \sqrt{\sum_{i=1}^n \sum_{j=1}^n \frac {(\delta_{ij}-d_{ij})^2} {\delta_{ij}^2}} \end{equation*}

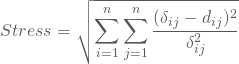
Einige Autoren verwenden andere Normierungsfaktoren im Nenner.

Im Fall der nicht-metrischen MDS mit ordinalskalierten Daten kannst Du die Unähnlichkeitsmaße nicht mit den Distanzen gleichsetzen, sondern ihre Rangfolgen sollten übereinstimmen.

In diesem Fall beginnst Du bei n Objekten, deren Konfiguration im m-dimensionalen Raum erstellt werden soll, mit einer (n x m)-Startkonfiguration, die entweder aus Zufallszahlen besteht oder in einem vorgeschalteten metrischen Verfahren ermittelt wurde.

Diese veränderst Du mit einem iterativen Verfahren schrittweise so, dass sich die Rangfolge der Interpunktdistanzen den Unähnlichkeitsmaßen annähert: Punktepaare (i,j), deren Rangwert des Unähnlichkeitsmaßes kleiner ist als der Rangwert Ihrer Distanzen, rückst Du näher zusammen bzw. im entgegengesetzten Fall schiebst Du sie weiter auseinander. Man spricht von der Durchführung einer monotonen Regression f(x) der Distanzen auf die Unähnlichkeitsmaße.

In jedem Schritt kannst Du den für den nicht-metrischen Fall modifizierten Stresswert berechnen und das Verfahren solange fortsetzen, bis Dein Wert ausreichend klein ist.

Hast Du Deine Konfiguration ermittelt, interpretierst Du am Ende die von Dir ermittelten Dimensionen. In der Regel benötigst Du dafür Zusatzinformationen, die ebenfalls von den Testpersonen erhoben werden.

Die Multidimensionale Skalierung wird beispielsweise in der Marktforschung zur Imageanalyse eingesetzt, wenn Du die Aussagen der Testpersonen nicht durch vorgegebene Urteilsskalen einschränken möchtest: Du erhebst dann von Deinen Testpersonen globale Unähnlichkeitsaussagen zwischen Deinem Produkt und den wichtigsten Konkurrenzprodukten und ermittelst daraus in einem passenden MDS-Verfahren eine meist zwei- oder dreidimensionale Konfiguration mit brauchbarem Stresswert. Diese zeigt Dir dann die visuelle Anordnung der betrachteten Produkte in den Augen Deiner Testpersonen.

Du kannst daraus entnehmen, welche anderen Produkte in direkter Konkurrenz zu Deinem Produkt stehen, sowie Nischen im Wahrnehmungsraum für neue Produktkonzeptionen ausmachen.