Hierarchisches lineares Modell – Multilevel Analyse – Mehrebenenanalyse

Hinter dem Begriff „Hierarchisches lineares Modell“ (HLM) verbirgt sich nichts anderes eine Form der linearen Regression. Die hierarchische lineare Modellierung taucht im Übrigen ebenso unter dem Begriff Mehrebenenanalyse (Multilevel-Analysis) auf. So lautet der Buchtitel von Robert Bickel zu dieser Thematik nicht ohne Grund „Multilevel Analysis for Applied Research: It’s just Regression“.

Was hat die hierarchische lineare Modellierung bzw. Mehrebenenanalyse mit linearer Regression gemeinsam?

Grundsätzlich geht es um Erstellung eines Modells zur Vorhersage der Ausprägung einer abhängigen Variable (Kriterium) mit Hilfe von unabhängigen Variablen (Prädiktoren). Link zu linearer Regression

Worin liegt der Unterschied?

Die Besonderheit liegt darin, Daten mit hierarchischer Struktur bzw. verschiedenen Ebenen auszuwerten. Hierarchische Daten erhältst Du beispielsweise bei Erhebungen von Schülern (untergeordnete Ebene 1) verschiedener Klassen (übergeordnete Ebene 2). Die meisten statistischen Verfahren behandeln Daten lediglich auf einer Ebene. Problematisch wird dies, wenn von dem Zusammenhang einer Ebene auf eine weitere Ebene geschlossen wird. Dies kann zu Fehlinterpretationen der Effekte und somit zu Fehlschlüssen führen. Am deutlichsten wird Dir dies am Beispiel des „Big-Fish-Little-Pond-Effect“ klar (s. unten).

Die hierarchische Struktur

Abbildung 1Meistens handelt es sich um 2 Ebenen, wobei Ebene 2 die übergeordnete und Ebene 1 die untergeordnete Ebene darstellt. Prädiktoren (UVs) können auf unterschiedlichen Ebenen liegen und für Vorhersagen dienen. Die abhängige Variable liegt dagegen immer auf Ebene 1. Grundsätzlich könnte man mit klassischen statistischen Methoden verschiedene Ebenen nacheinander auswerten. Die HLM bietet Dir den großen Vorteil, diese Auswertungen auf einmal und simultan durchzuführen. So kannst Du Fehlschlüsse vermeiden bzw. reduzieren. Zudem liefert nur die hierarchische lineare Modellierung eine unverzerrte Schätzung von Standardfehlern bezüglich hierarchischer Daten.

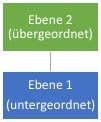
Abbildung 1

 

Hierarchischer Daten

Abbildung 2

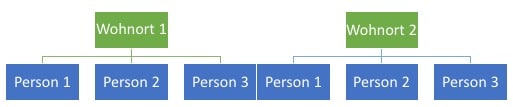
Abbildung 3

Tagebuchstudien

Ein weiteres häufiges Einsatzgebiet der Mehrebenenanalyse ist die Auswertung von Tagebuchstudien, wobei Ebene 2 die verschiedenen Individuen beinhaltet und Ebene 1 die Messzeitpunkte darstellt. Für weitere Informationen ist das Buch Intensive Longitudinal Methods von Bolger & Laurenceau (2013) zu empfehlen.

Abbildung 4

 

Beispiel: „Big-Fish-Little-Pond-Effect“

Im Folgenden siehst Du anhand eines Beispiels, dass Effekte in Abhängigkeit von der analysierten Ebene variieren können. Der „Big-Fish-Little-Pond-Effect“, auch Fischteicheffekt, ist ein aus der pädagogischen Psychologie stammendes Phänomen (siehe Abbildung 4, idealtypische Darstellung) und betrifft den Effekt, dass gleichgute Schüler verschiedener Schulen eine sehr unterschiedliche subjektive Einschätzung ihrer Fähigkeiten haben können. Dies scheint abhängig vom Vergleich mit ihren Mitschülern zu sein.

• Schüler A und Schüler B haben die gleiche objektive Schulleistung
• Schüler A in Little Pond = leistungsschwache Mitschüler => hohe Selbsteinschätzung (Big Fish)
• Schüler B in Big Pond = leistungsstarke Mitschüler => geringe Selbsteinschätzung (Little Fish)
• Schlussfolgerung: Je höher die Schulleistung (Big Pond), desto geringer die Selbsteinschätzung (little Fish), bei gleicher Schulleistung

Intuitiv ist eine bessere Schulleistung jedoch mit einer ebenso besseren Selbsteinschätzung akademischer Fähigkeiten verbunden. Und auch dies trifft tatsächlich zu.

Zunächst ist es auffallend, dass beim Vergleich verschiedener Schulen, ein Schüler einer leistungsstarken Schule ein geringeres akademisches Selbstkonzept aufweist, als ein Schüler einer leistungsschwächeren Schule (Ebene 2). Auf Ebene 2 (Schul-Ebene) ist eine bessere Schulleistung also negativ mit dem akademischen Selbstkonzept assoziiert. Auf Ebene 1 (Schüler-Ebene) hängt, wie zu erwarten, eine bessere Schulleistung positiver mit dem akademischen Selbstkonzept zusammen.

Dieses Beispiel zeigt, dass auf verschiedenen Analyseebenen sogar ein entgegengerichteter Effekt herrschen kann. Häufig unterscheidet sich mindestens die Stärke des Effektes auf den unterschiedlichen Ebenen. Die Effekte (Steigungen) innerhalb der Schulen (blau) können übrigens unterschiedlich stark sein, wie Du im folgenden Abschnitt sehen wirst.

In Abbildung 4 ist konzeptuell dargestellt, was die Mehrebenenanalyse hervorbringt. Du siehst vier lineare Regressionen (eine Regression mit negativem Effekt auf Ebene 2 (grün) und drei weitere mit positivem Effekt auf Ebene 1 (blau)).

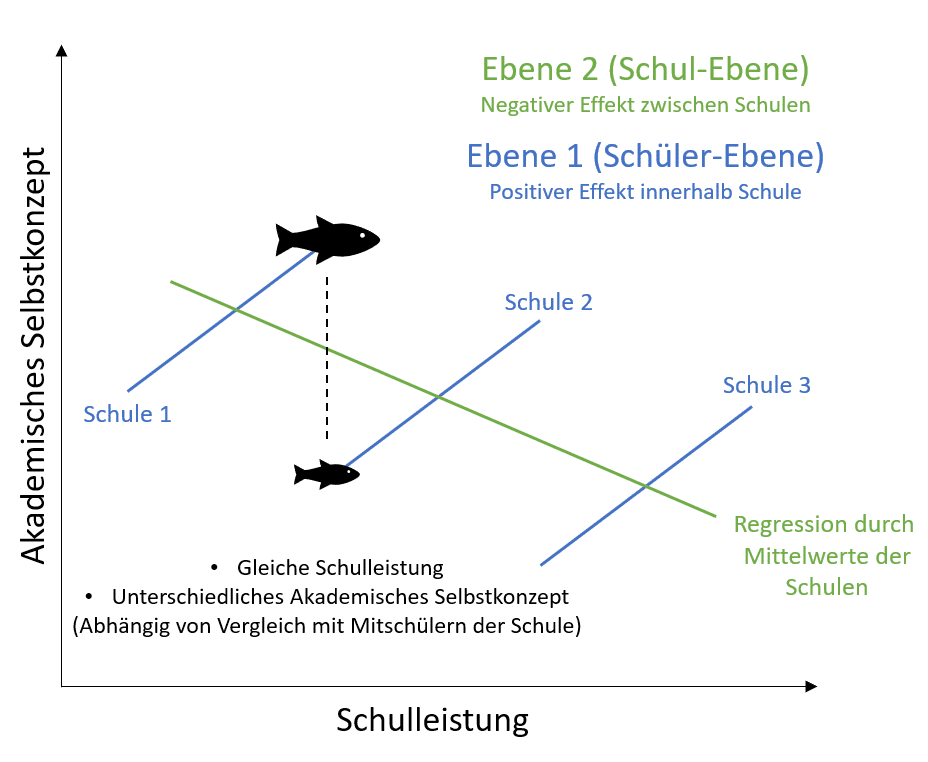Abbildung 5

Zufällige und feste Effekte (random and fixed effects)

Bei der normalen linearen Regression gibt es ausschließlich feste Effekte (fixed effects). Wir haben genau einen Achsenschnittpunkt und eine Steigung.

Bei der Multilevel-Analyse gibt es zusätzlich folgende Besonderheit. Wir können untersuchen, ob auf Ebene 1, also innerhalb der Schulen 1) unterschiedliche Achsenschnittpunkte (Intercepts) oder 2) Steigungen (Slopes) die Varianz der Daten erklären können, um ein bestmöglich passendes Modell mit verallgemeinerbaren Parametern schätzen zu können. Was Du dir darunter vorstellen kannst, siehst Du in Abbildung 6 und 7.

Abbildung 6 illustriert ein Modell mit zufälligem Achsenschnittpunkt und zufälligem Effekt auf Ebene 1. Das Modell hat für die zugrundeliegenden Daten den besten „fit“, wenn auf Ebene 1 beide random effects zugelassen werden. Die Schulen unterscheiden sich sowohl im Zusammenhang zwischen Schulleistung und akademischem Selbstkonzept, als auch im Ausmaß des akademischen Selbstkonzeptes für den Schulleistungswert 0.

Dies wird vor der Berechnung festgelegt. Das Modell mit dem besten Fit kann nach und nach angepasst werden, sofern keine feste Hypothese besteht.

In Abbildung 7 siehst du dagegen ein Modell mit festem Achsenschnittpunkt und zufälligem Effekt. Die Schulen unterscheiden sich hinsichtlich der Stärke des Effekts, wobei der Schulleistungswert 0 mit dem gleichen Ausmaß an akademischem Selbstkonzept assoziiert ist.

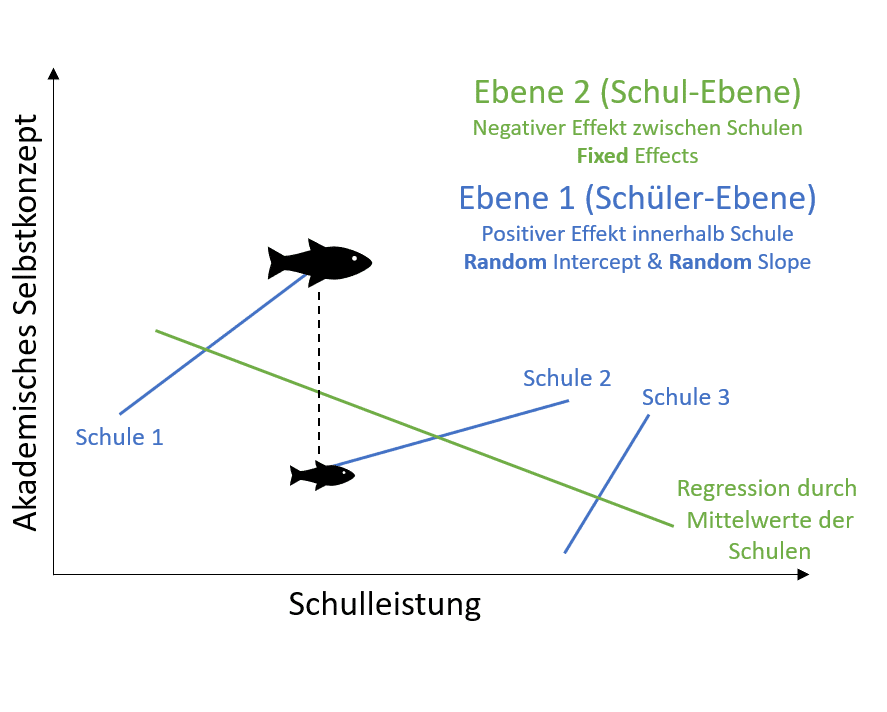
Abbildung 6

 

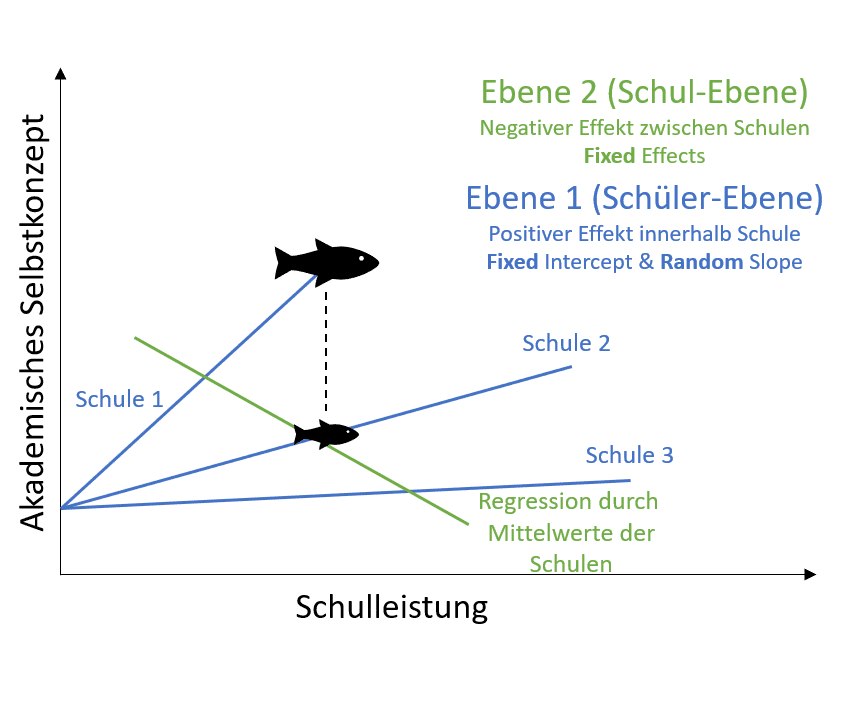
Abbildung 7

Voraussetzungen für die Mehrebenenanalyse

Insbesondere ist hier die Unabhängigkeit und Normalverteilung der Residuen auf Ebene 1 wichtig. Das heißt, innerhalb der Schule muss stochastische Unabhängigkeit herrschen. Die Abhängigkeit, welche durch die Zuordnung der Schüler zu einer Schule entsteht, ist dagegen kein Problem und somit ein großer Vorteil der Mehrebenenanalyse. Unabhängigkeit und multivariate Normalverteilung der Ebene 2 Residuen ist zwar ebenso eine Voraussetzung, muss jedoch angenommen werden, da sie im Grunde nicht überprüfbar ist.

Die Verletzung der Normalverteilungsannahme kommt in der Realität häufig vor. Diese Verletzung der Annahme wirkt sich auf die Standardfehler aus. Die Standardfehler können jedoch auch korrigiert werden, was beispielsweise mit dem Programm HLM möglich ist (Die Stichprobengröße auf Ebene 2 sollte in diesem Fall relativ groß sein: n > 100).

Zusammenfassung

Wie Du gesehen hast, ist die hierarchische lineare Modellierung bzw. Mehrebenenanalyse eine statistische Methode zur Auswertung hierarchischer Daten, welche in der Realität häufig vorkommen. Klassische statistische Verfahren, wie die lineare Regression, betrachten lediglich eine Ebene. Hierdurch vernachlässigst Du immer einen Teil der Realität oder ziehst sogar Fehlschlüsse. Der Vorteil der Mehrebenenanalyse besteht darin, Effekte auf verschiedenen Ebenen zu berücksichtigen und simultan zu berechnen. Zur Auswertung kannst Du verschiedene Programme verwenden, z.B. SPSS, Stata oder R. Ein spezielles Programm für Hierarchische lineare Modelle ist beispielsweise HLM5.

Literaturempfehlung:

Bolger, N. & Laurenceau, J.-P. (2013). Intensive longitudinal methods. An introduction to diary and experience sampling research. New York, London: The Guilford Press.

Hox, J. J. (2010). Multilevel analysis. Techniques and applications. New York: Routledge.