Korrespondenzanalyse

Korrespondenzanalyse

  • 26. April 2018
  • Posted by: Mika
Keine Kommentare

Mit der Korrespondenzanalyse kannst Du Beziehungen zwischen zwei mindestens nominalskalierten Variablengruppen visuell darstellen. So kannst Du zum Beispiel in der Marktforschung eine Gruppe von Produkten, zu denen Du bestimmte Eigenschaften erhoben hast, in einer zweidimensionalen Ebene so abbilden, dass die Distanzen den Unterschieden in den Eigenschaften entsprechen. Dazu reduzierst Du die Anzahl der beschreibenden Faktoren in der Regel auf zwei.

Man spricht daher auch von nicht-metrischer Faktoren- oder Hauptkomponentenanalyse.

Das Verfahren erfolgt in drei Schritten:

Im ersten Schritt erstellst Du aus Deinen Daten eine Kontingenztabelle und berechnest den zugehörigen \chi^2-Prüfwert.

Im zweiten Schritt extrahierst Du die Dimensionen so, dass Du einerseits möglichst wenig Dimensionen erhältst (das menschliche Auge kann nicht mehr als drei Dimensionen sehen, am besten überschaubar sind für uns zwei Dimensionen), andererseits aber möglichst wenig Information dabei verloren geht.

Im dritten Schritt normalisierst Du die Koordinaten symmetrisch und interpretierst die Dimension.

Als Beispieldaten dienen die Ergebnisse eines Tests zu Waschmitteln. Vier konkurrierende Waschmittel x_i,i=1,..,4 wurden bezüglich drei Kriterien y_j, j=1,…3 untersucht und sie erhielten Punkte zwischen 1 und 40. Es ergaben sich die folgenden Ergebnisse:

Y_j
j 1 2 3
i n_{ij} Waschwirkung Textilschonung Umwelteigenschaften Zeilensummen
n_{i \cdot}
      X_i       1 Wasch Gerne 11 2 36 49
2 Sauber und Gut 17 45 27 89
3 Bravo Wasch 38 28 15 81
4 Ultra Sauber 23 37 32 92
Spaltensummen
n_{\cdot j}		 89 112 110 311

Mit Hilfe der Zeilen- und Spaltensummen kannst Du die erwarteten Anzahlen berechnen, die sich im Fall von Unabhängigkeit ergeben würden, als

    \begin{equation*} \hat n_{ij} = \frac {n_{\cdot j} \cdot n_{i \cdot}}{n} \end{equation*}

Du erhältst die folgende Tabelle:

Y_j
j 1 2 3
i \hat n_{ij} Waschwirkung Textilschonung Umwelteigenschaften Zeilensummen
n_{i \cdot}
      X_i      1 Wasch Gerne 14,02 17,65 17,33 49
2 Sauber und Gut 25,47 32,05 31,48 89
3 Bravo Wasch 23,18 29,17 28,65 81
4 Ultra Sauber 26,33 33,13 32,54 92
Spaltensummen
n_{\cdot j}		 89 112 110 311

Daraus berechnest Du die normierten Differenzen z_{ij}zwischen den n_{ij} und den \bar n_{ij}, dividiert durch \sqrt {\bar n_{ij}}:

    \begin{equation*} z_{ij} = \frac {n_{ij} - \hat n_{ij} } {\sqrt{\hat n_{ij}}} \end{equation*}

Quadrierst Du die z_{ij} über alle i und alle j, so erhältst Du die \chi^2-Prüfgröße der Kontingenzanalyse zu

    \begin{equation*} \chi^2 = \sum_{i=1}^I \sum_{j=1}^J z_{ij}^2 = \sum_{i=1}^I \sum_{j=1}^J \frac {(n_{ij} - \hat n_{ij})^2 } {\hat n_{ij}} = 60,2252 \end{equation*}

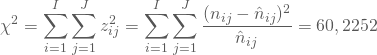
Die Prüfgröße folgt einer \chi^2-Verteilung mit \nu=(I-1)\cdot(J-1)=3\cdot 2=6 Freiheitsgraden.

Sie ist allerdings abhängig von der Gesamtanzahl n Deiner Erhebung. Um diesen Effekt zu bereinigen, berechnest Du die Total Inertia T als Quotient aus \chi^2 und n,

    \begin{equation*} T= \frac {\chi^2}{n}=\frac {60,2252}{311}=0,1936 \end{equation*}

T liegt zwischen Null und (k-1), wobei k der kleinere der beiden Werte I und J ist. In Deinem Beispiel liegt T also zwischen Null und Zwei.

Im zweiten Schritt der Analyse geht es um die Reduzierung der Dimensionen. Dazu zerlegst Du die (I x J)-dimensionale Matrix Z =(z_{ij}) mittels Singularwertzerlegung in:

    \begin{equation*} Z\quad=\quad U \quad \cdot\quad S \quad \cdot \quad V \end{equation*}

Dabei sind

Z = (z_{ij}) die (I x J)- Matrix der standardisierten Häufigkeitsdifferenzen
U = (u_{ik}) die (I x K)- Matrix der Zeilenelemente
S = (s_{kk}) die (K x K)- Diagonalmatrix der Singularwerte
V = (v_{kj}) die (K x J)- Matrix der Spaltenelemente

Du erhältst die Diagonalelemente s_k von S als positive Quadratwurzel der Eigenwerte \lambda_k der Matrix Z^T \cdot Z. Hier sind \lambda_1=0,1396 und\lambda_2= 0,0540.

Die Summe der Eigenwerte ist gleich dem Wert der oben berechneten Total Inertia T=0,1936; ihr Anteil an der Total Intertia \frac {\lambda_k}{T} drückt den prozentualen Beitrag aus, den der k-te Faktor zur Erklärung der Beobachtungen leistet. Demnach trägt der erste Faktor mit \frac {\lambda_1} T=72,0732 \%, der zweite Faktor mit \frac {\lambda_2} T=27,68 \% zur Erklärung der Beobachtungen bei.

Die Matrizen V und U ergeben sich aus den zu den Eigenwerten zugehörigen Eigenvektoren; sie sind nicht eindeutig bestimmt.

Im dritten Schritt werden U und V daher normiert, üblicherweise wählt man eine symmetrische Normierung. Dann kannst Du die Koordinaten der Realisationen von (abhängigen) Variablen X_i und ursprünglichen (unabhängigen) Merkmalen Y_j als

    \begin{equation*} x^*_{ik}= \frac {u_{ik} \cdot \sqrt{s_k}}{\sqrt{p_{i \cdot}} } \quad und \quad y^*_{jk}= \frac {v_{jk} \cdot \sqrt{s_k}}{\sqrt{p_{\cdot j}} }, \end{equation*}

berechnen, mit

    \begin{equation*} p_{i \cdot}={\sqrt{\frac {n_{i \cdot}}n} }\quad und \quad p_{\cdot j}={\sqrt{\frac {n_{ \cdot j}}n} }\end{equation*}

Die Grafik zeigt das Ergebnis der Korrespondenzanalyse für das Beispiel des Waschmitteltests:

Korrespondenzanalyse

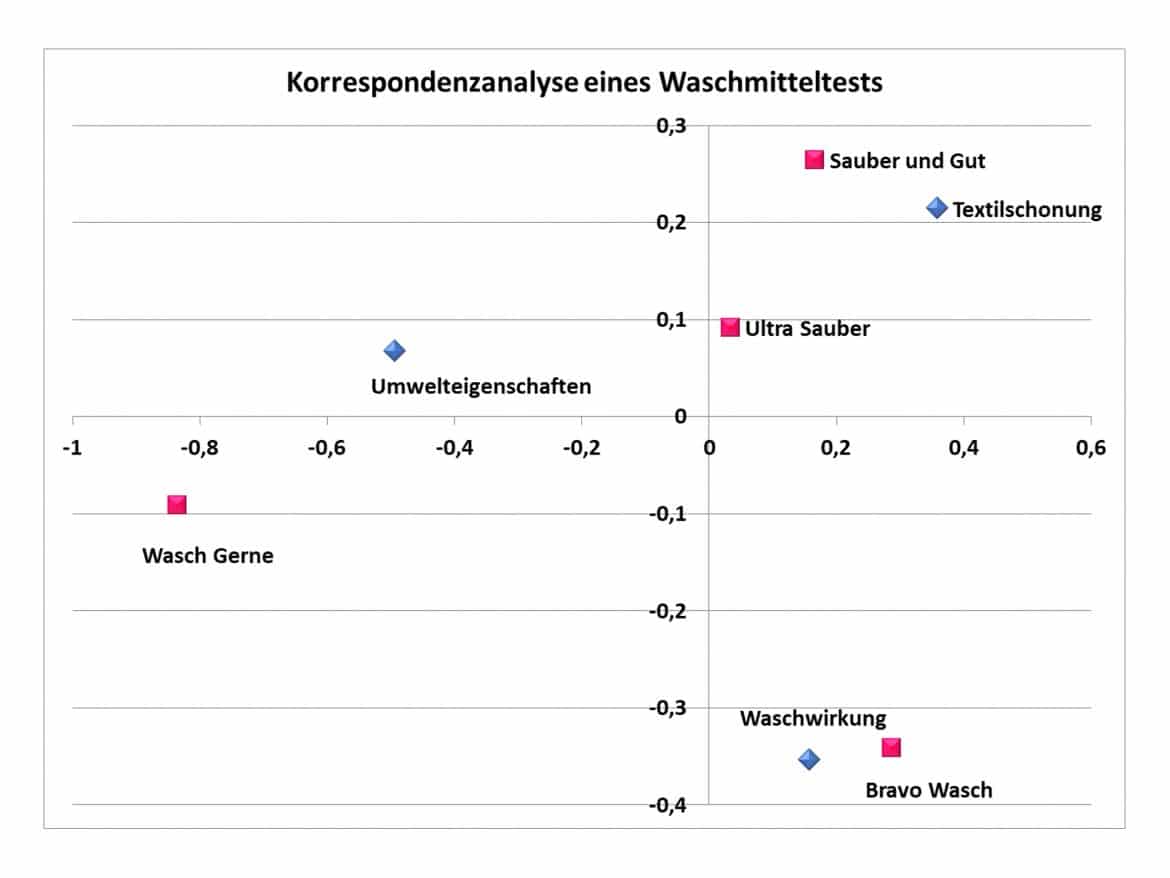
Am Ende bleibt Dir die Interpretation der Grafik. Die Durchschnittsprofile liegen im Ursprung des Koordinatensystems. Je weiter eine Beobachtung vom Ursprung entfernt liegt, desto stärker unterscheidet sie sich in der Wahrnehmung der Probanden vom Durchschnitt; je näher zwei Beobachtungen zueinander liegen, desto ähnlicher sind sie.

Es erstaunt nicht, dass Waschwirkung und Umwelt-bzw. Textilschonung in entgegengesetzter Richtung auf der vertikalen Achse abgetragen sind; möglicherweise drückt diese Achse den Anteil von chemischen Flecklösern aus. Die horizontale Achse, gibt an, ob ein Waschmittel eher als umweltfreundlich oder textilschonend wahrgenommen wird.