Hauptkomponentenanalyse PCA

Die Hauptkomponentenanalyse (engl. für Principal Component Analysis, PCA) wendest Du an, wenn Du einen großen Datensatz strukturieren bzw. vereinfachen möchtest. Dabei versuchst Du die Gesamtzahl Deiner gemessenen Variablen zu reduzieren und trotzdem einen möglichst großen Anteil der Varianz aller Variablen zu erklären.

Diese Reduktion erfolgt mathematisch gesehen über Linearkombinationen, aus denen die Hauptkomponenten resultieren. Du kannst Dir diese Linearkombinationen als Gerade zwischen den Variablenwerten vorstellen, ähnlich wie eine Regressionsgerade. Das bedeutet, die PCA arbeitet rein explorativ und sucht in den Daten ein lineares Muster, das Deinen Datensatz bestmöglich beschreibt.

Wie entstehen die Hauptkomponenten?

Die erste Hauptkomponente entsteht durch Minimierung der Summe der quadrierten Abweichungen aller Variablen. In anderen Worten wird zur Extraktion der ersten Komponente der Varianzanteil, den die Komponente über alle Variablen hinweg erklären kann, maximiert. Danach wird schrittweise versucht die verbleibende Varianz aufzuklären. Das heißt die zweite Komponente soll so viel Restvarianz wie möglich aufklären. Dieses Verfahren wird so lange weitergeführt, bis theoretisch die Gesamtvarianz all Deiner Daten durch die Hauptkomponenten erklärt ist.

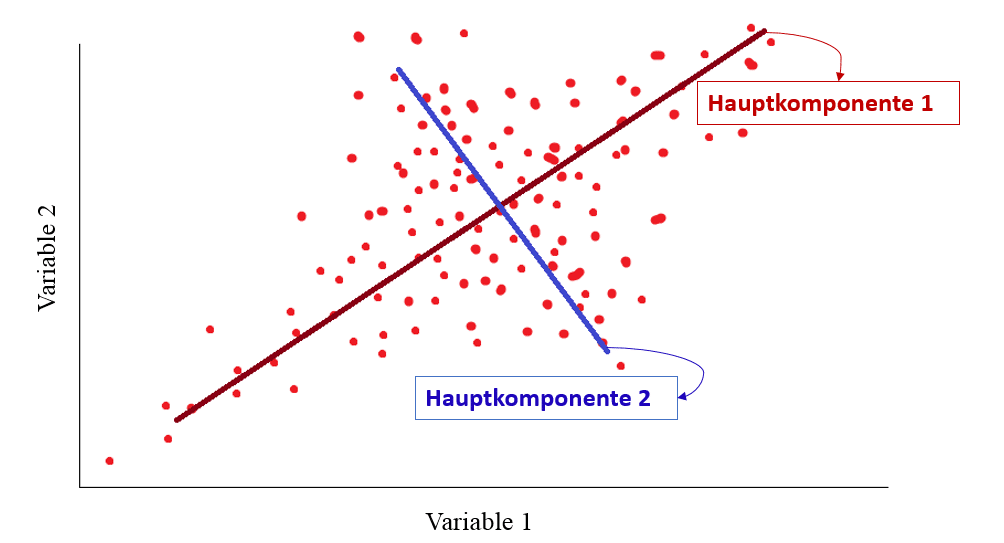
In der nachfolgenden Abbildung ist die Funktionsweise der Hauptkomponentenanalyse schematisch dargestellt. Die Kleinstquadratmethode legt die rote Gerade durch die Datenwolke und bildet die Hauptkomponente 1. Hauptkomponente 2 resultiert aus der blauen Geraden, welche Varianz aufklärt, die durch die erste Hauptkomponente kaum erfasst werden kann.

Wie viele Komponenten sind das Ziel?

Die Zahl Deiner extrahierten Komponenten ergibt sich aus dem Datensatz. Weniger relevante Komponenten kannst Du trotzdem meist ohne großen Informationsverlust einfach weglassen, da sie hauptsächlich Rauschen in Deinen Daten beschreiben. Würde man aus der Datenwolke in der oben erwähnten Abbildung bspw. 5 oder 6 Komponenten extrahieren, ist es ziemlich unwahrscheinlich, dass diese noch viel zur Varianzaufklärung beitragen.

Die exakte mathematische Theorie hinter der PCA ist recht komplex. Um die Methode korrekt anzuwenden, ist es nicht zwangsläufig notwendig die statistische Modellierung tiefgreifend zu verstehen, die Anforderungen an Deine Daten sollten aber erfüllt sein.

Voraussetzungen für eine PCA

Bevor Du eine PCA berechnest, solltest Du daher wie immer die entsprechenden Voraussetzungen prüfen. Die PCA ist nur dann ein zuverlässiges Verfahren, wenn Deine Daten zumindest intervallskaliert und annähern normalverteilt sind. Außerdem ist es wichtig zu beachten, dass die PCA die Fehler- und Residualvarianz Deiner Daten nicht berücksichtigt. Sie bereinigt die Variablen lediglich hinsichtlich redundanter Effekte (Interkorrelationen).

Die meisten in psychologischen oder sozialwissenschaftlichen Studien erhobenen Daten enthalten aber einen gewissen Anteil an Fehlervarianz, weshalb Du die PCA eigentlich nicht zur Analyse solcher Datensätze anwenden solltest, da sie Dir ungenaue Resultate liefert. Sehr gut geeignet ist die PCA bspw. für die Bildverarbeitung oder für die Analyse neuronaler Netze, da zur Gruppierung von Daten im Rahmen dieser Anwendungsgebiete die Berücksichtigung von Fehler- bzw. Residualvarianzen nicht erforderlich ist.

Trotzdem ist die PCA auch in den Sozialwissenschaften ein beliebtes Verfahren, das bspw. standardmäßig zur Faktorenextraktion bei der Faktorenanalyse eingesetzt wird. Manchmal werden PCA und Faktorenanalyse nicht klar voneinander unterschieden oder sogar synonym verwendet.

Die Faktorenanalyse umfasst im Gegensatz zur PCA jedoch eine ganze Reihe von Verfahren, wohingegen die PCA eine bestimmte Methode bezeichnet. Zudem ist es bei der PCA bspw. nicht möglich, inferenzstatistische Aussagen über die Gesamtpopulation zu treffen. Die konfirmatorische Faktorenanalyse dagegen basiert auf einem Modell sowie theoretischen Ableitungen. Durch ihr breit gefächertes Methodenrepertoire lässt sie sehr wohl Rückschlüsse auf eine Grundgesamtheit zu.