Faktorenanalyse

Die Faktorenanalyse ist ein Verfahren, mit dem Du Strukturen in Deinen Daten untersuchen kannst, indem Du eine Vielzahl von Variablen auf eine geringere Anzahl an Faktoren reduzierst, die dafür aber zentraler sind. Diese Reduzierung kann auf zweierlei Art erfolgen.

Einerseits kannst Du explorativ vorgehen und mathematisch nach der der besten Lösung suchen, ohne Dich inhaltlich an einer bestimmten Theorie zu orientieren (= explorative Faktorenanalyse).

Andererseits kannst Du mit Hilfe der konfirmatorischen Faktorenanalyse hypothesengeleitet testen, ob ein von Dir aufgestelltes Modell anhand Deiner Daten bestätigt wird oder nicht. Mit einem Modell sind in diesem Fall theoretische Vorüberlegungen gemeint, die sich damit befassen, inwiefern Du verschiedene Variablen zu einem Faktor zusammenfassen kannst.

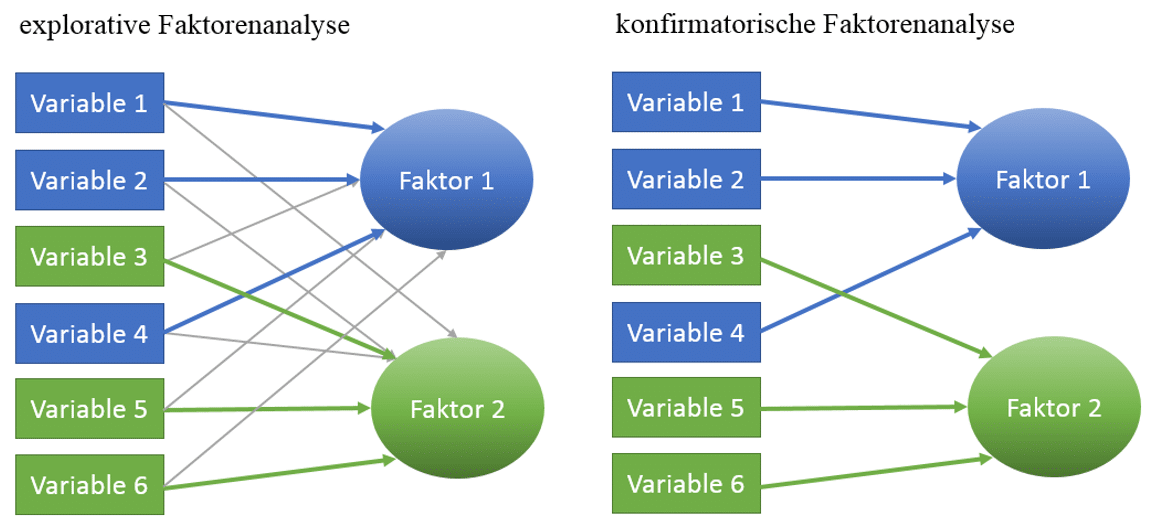
Unterschied zwischen explorativer und konfirmatorischer Faktorenanalyse

In der nachfolgenden Abbildung sind die Unterschiede zwischen explorativer und konfirmatorischer Faktorenanalyse schematisch dargestellt. Bei der explorativen Faktorenanalyse untersuchst Du, wie gut jede einzelne Variable zu allen Faktoren passt. Beispielsweise könntest Du dann feststellen, dass sich Deine Variablen 1, 2 und 4 mathematisch betrachtet am besten zu Faktor 1 zusammenfassen lassen. Deine Variablen 3, 5 und 6 passen z. B. besser zu Faktor 2. Anhand der grauen Pfeile in der Abbildung ist ersichtlich, dass aber z. B. auch berechnet wurde, wie gut Variable 1 zu Faktor 2 passt.

Bei der konfirmatorischen Faktorenanalyse führst Du Deine Berechnungen aufgrund von Hypothesen durch und könntest bspw. testen, ob das Datenmuster Deinen Vorüberlegungen entspricht und wie gut die Variablen 1, 2 und 4 einen gemeinsamen Faktor widerspiegeln bzw. die Variablen 3, 5 und 6 einen zweiten Faktor. Inwiefern Variable 3 zu Faktor 1 passt, würdest Du mit dieser Methode nicht überprüfen (ersichtlich anhand der fehlenden grauen Pfeile).

Hintergrund der Faktorenanalyse

Die Faktorenanalyse basiert auf multivariaten Verfahren, d. h. sie setzt mehrere AVs zueinander in Bezug. Ziel ist es, diese AVs so zusammenzufassen, dass Du Faktoren bildest, die möglichst wenig miteinander wechselwirken. Anders ausgedrückt, jene AVs, die stark miteinander korrelieren, werden zu einem Faktor zusammengefasst. Ein Faktor ist demnach ein rein theoretisches Konstrukt, das Informationen aus mehreren zusammenhängenden Variablen enthält.

Welche Variable welchem Faktor zugeteilt wird und wie gut sie zu diesem Faktor passt, kannst Du der sogenannten Faktorladung ablesen. Die Faktorladung kann zwischen +1 und -1 liegen und je näher die Faktorladung einer Variablen an einer dieser beiden Grenzen liegt (also je weiter sie zahlenmäßig von Null entfernt ist), desto stärker lädt sie auf den Faktor.

Ein weiterer Begriff den Du im Rahmen der Faktorenanalyse kennen solltest, ist die Kommunalität. Die Kommunalität gibt Dir an, wie stark welcher Faktor zur Varianzaufklärung jeder einzelnen Variable beiträgt. Die maximale Kommunalität ist 1 – würde Die Kommunalität eines Faktors in Bezug auf eine einzelne Variable 1 betragen, wären damit quasi 100 % der Varianz der Variablen durch den Faktor aufgeklärt.

Vorsicht allerdings, dass Du die Kommunalität nicht mit dem Eigenwert verwechselst. Der Eigenwert bezieht sich nämlich auf die Faktoren und gibt an, wie viel Varianz insgesamt (über alle Variablen hinweg) durch einen Faktor aufgeklärt wird.

Damit Du eine Faktorenanalyse berechnen kannst, die valide Ergebnisse liefert, muss Dein Datensatz folgende Voraussetzungen erfüllen:

Voraussetzungen für eine Faktorenanalyse

• Deine Variablen müssen normalverteilt sein
• Deine Variablen sollten intervallskaliert sein (dichotome Variablen darfst Du nur unter Vorbehalt verwenden).
• Pro Variable solltest Du mindestens 10 Fälle erhoben haben
• Es müssen ausreichend Variablen vorhanden sein (pro Faktor vier oder mehr Variablen)

Sind alle Voraussetzungen erfüllt, gibt es verschiedene Möglichkeiten, mit denen Du aus Deinem Datensatz Faktoren extrahieren kannst. Prinzipiell funktioniert die Faktorenextraktion nach dem Prinzip, dass jeder Faktor so viel Varianz in den Daten erklären soll, wie möglich. Zwei sehr gebräuchliche Verfahren um die Faktorenextraktion durchzuführen, sind die Hauptkomponentenanalyse und die Hauptachsenanalyse.

Wie viele Faktoren Du extrahierst, kannst Du entweder inhaltlich aus der Theorie ableiten. Oder Du legst  fest, wie viel ein Faktor zur Varianzaufklärung beitragen muss, damit er in Dein Modell aufgenommen wird. Alternativ kannst Du auch nach dem Eigenwertkriterium (= Kaiser-Guttman-Regel) vorgehen, derer zufolge alle Faktoren aufgenommen werden, die einen Eigenwert größer 1 aufweisen, da der Faktor dann auf jeden Fall mehr Varianz erklärt, als eine einzelne Variable.

Interpretation der Ergebnisse

Es ist relativ einfach die Faktorenanalyse durchzuführen, schwierig ist jedoch die extrahierten Faktoren inhaltlich zu interpretieren. Die Faktorenanalyse gibt Dir ein rein mathematisches Modell aus, bietet aber keinerlei Hilfestellung, wie dieses zu interpretieren ist. Explorativ wird das Verfahren daher vor allem hypothesengenerierend eingesetzt. Die konfirmatorische Faktorenanalyse findet bspw. bei der Entwicklung von Messinstrumenten Anwendung. Denn diese beruhen auf akribischen theoretischen Ableitungen. Zudem gibt es genaue Hypothesen, welche Variablen sich zu welchem Faktor zusammenfassen lassen.