Diskriminanzanalyse

Diskriminanzanalyse

  • 26. April 2018
  • Posted by: Mika
Keine Kommentare

Die Diskriminanzanalyse umfasst statistische Verfahren, mit denen Du eine abhängige nominalskalierte Variable aufgrund von metrisch-skalierten unabhängigen Variablen erklären und prognostizieren kannst.

Stell Dir vor, die Käufer Deines Produktes gliedern sich in die Gruppen markentreue Kunden (M) und Markenwechsler (W), die Du jeweils mit speziellen Marketinginstrumenten ansprechen möchtest. Aus vorherigen Analysen weißt Du, dass sich die beiden Gruppen bezüglich Einkommen (X_1) und durchschnittlicher Einkaufszeit pro Woche (X_2) unterscheiden.

Du suchst nun eine Funktion als Kombination von X_1 und X_2, die Diskriminanzfunktion, die eine möglichst scharfe Trennung zwischen den Gruppen M und W ermöglicht: Danach, in welches Intervall der Diskriminanzwert eines Käufers fällt, erfolgt seine Zuordnung.

Am Ende bestimmst Du die Trennschärfe Deiner Funktion.

Für obiges Beispiel hast Du Einkommen und durchschnittliche wöchentliche Einkaufszeit von 22 Testkäufern ermittelt:

Markentreue Kunden
lfd. Nr. i 1 2 3 4 5 6 7 8 9 10 11
Einkommen
in T€		 x_1 3,2 2,5 1,5 3,5 2,5 3,5 3,0 1,0 3,5 2,5 3,5
Wöchentliche Einkaufszeit
in Std.		 x_2 0,5 0,5 0,5 1,0 1,0 1,5 1,5 1,5 2,0 2,0 2,5
Zuordnung nach dem Diskriminanzwert M M M M M M M W M W M
Markenwechsler
lfd. Nr. i 1 2 3 4 5 6 7 8 9 10 11
Einkommen
in T€		 x_1 1,0 2,0 1,5 0,8 2,5 2,0 1,0 3,0 1,5 1,5 2,2
Wöchentliche Einkaufszeit
in Std.		 x_2 0,7 1,0 2,0 2,0 2,5 2,5 2,5 3,0 3,0 2,5 3,0
Zuordnung nach dem Diskriminanzwert W M W W W W W W W W W

Die Grafik zeigt die Testkäufer im Koordinatensystem mit den Achsen „Einkommen“ und „Wöchentliche Einkaufszeit“:

Diskriminanzanalyse

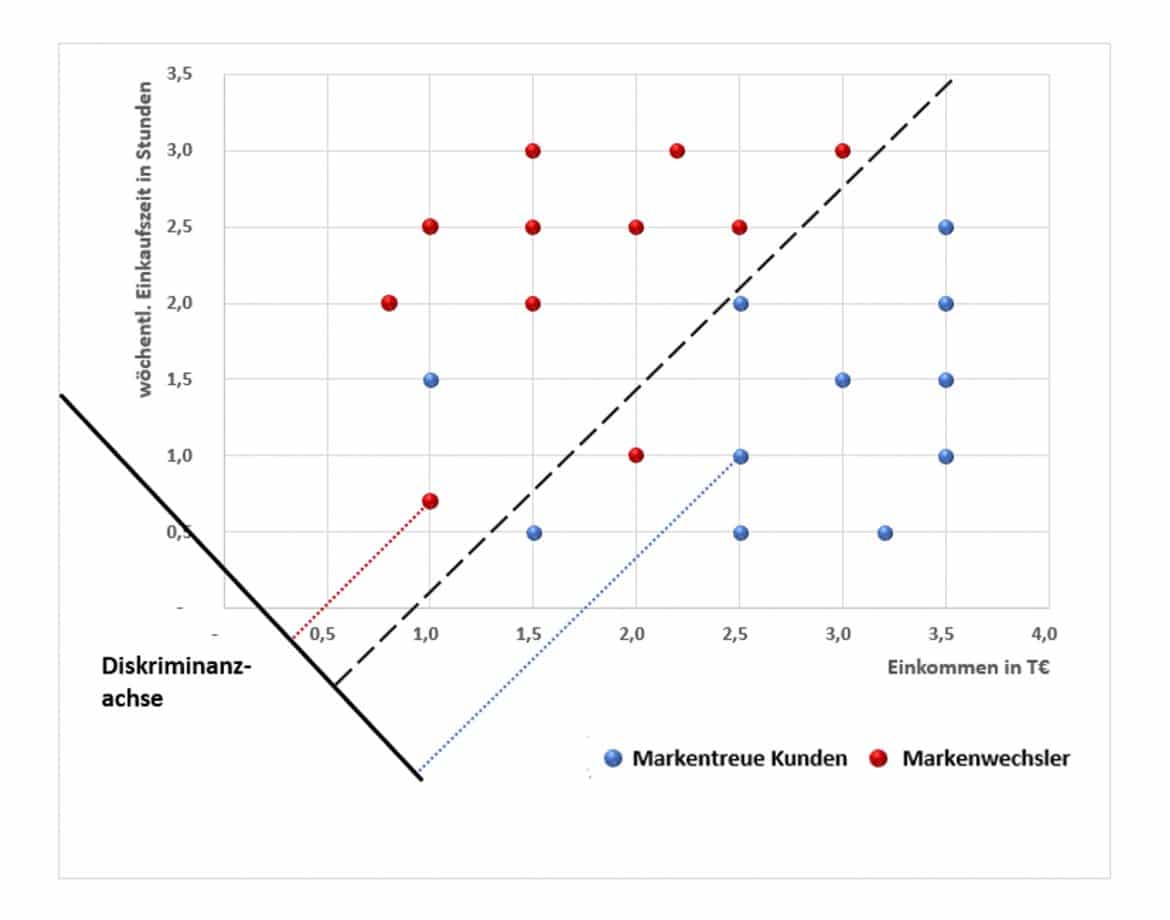
Gesucht ist nun als erstes eine Linie, die die blaue Punktwolke (Markentreue Kunden) möglichst gut von der roten Punktwolke (Markenwechsler) trennt: diese hast Du mit der schwarzen gestrichelten Linie in der Grafik gegeben. Deren Senkrechte ist dann Deine Diskriminanzachse: Projizierst Du einen Käufer-Punkt senkrecht auf die Diskriminanzachse, so erhältst Du seinen Diskriminanzwert, aus dem ermittelt wird, welcher Gruppe er zugeteilt wird: Liegt ein Diskriminanzwert oberhalb des Schnittpunktes, erfolgt eine Klassifizierung zu W, anderenfalls zu M.

Auf diese Weise kannst Du die Informationen aus den unabhängigen Variablen auf einen einzigen Wert verdichten; eine entsprechende Klassifizierung ist in der obigen Tabelle jeweils in der unteren Zeile erfolgt.
Allgemein lautet Deine lineare Diskriminanzachse:

    \begin{equation*} Y=a_1 \cdot X_1+a_2 \cdot X_2 \end{equation*}

Die Koeffizienten a_1 und a_2 werden so bestimmt, dass der Quotient aus den quadratischen Abweichungen zwischen den Gruppen M und W und der Summe der quadratischen Abweichungen innerhalb der Gruppen maximal wird:

    \begin{equation*} \lambda=\frac {(\bar y_M - \bar y_W)^2} {\displaystyle\sum_{i=1}^{n_M}(y_{iM}- \bar y_M)^2+ \displaystyle\sum_{i=1}^{n_W}(y_{iW}- \bar y_W)^2} } \to Max! \end{equation*}

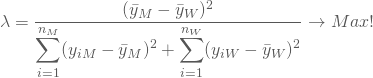
Bewertung Deiner Analyse:

Für die Bewertung Deiner Diskriminanzanalyse stehen verschiedenen Varianten zur Verfügung.

Zum einen kannst Du die Fehlklassifikationsrate berechnen: Die letzte Zeile der obigen Tabelle zeigt die Zuordnung der einzelnen Testkäufer nach der Diskriminanzfunktion, die Du auch in der Grafik erkennen kannst: In jeder Gruppe gibt es eine Fehlzuordnung, alle übrigen Käufer wurden durch Deine Diskriminanzfunktion richtig klassifiziert.

Für Dein Beispiel lautet damit die Fehlklassifikationsrate

    \begin{equation*} FKR = \frac 2 {22} = 9,09 \% \end{equation*}

was angesichts der kleinen Stichprobe kein schlechtes Ergebnis darstellt.

Wilks´Lambda \Lambda als Quotient der Determinaten von

  • W (Matrix der Quadratsummen von Abweichungen innerhalb der Gruppen) und
  • T (Matrix der Qudratsummen der Gesamtabweichungen)

stellt ein Maß für die Unterschiedlichkeit der beiden Gruppen dar:

    \begin{equation*} \Lambda=\frac {det (W)} {det (T)} \approx \frac {Abweichungen \nobreakspace innerhalb \nobreakspace der \nobreakspace Gruppen}{Gesamtabweichungen } \end{equation*}

\LAMBDA kann Werte zwischen Null und Eins annehmen. Je kleiner \Lambda, umso geringer ist der Anteil der durch Abweichungen innerhalb der Gruppen erklärte Teil der Gesamtabweichungen und umso größer ist der durch die Gruppenbildung erklärte Anteil: Umso besser vermag also die Diskriminanzfunktion die Gruppen zu trennen.

Mithilfe eines \chi^2-Tests kannst du prüfen, ob die mit Deiner Diskriminanzfunktion erreichte Trennung signifikant ist, ob also signifikante Mittelwertunterschiede zwischen den Gruppen bestehen.

    \begin{equation*} \chi^2_{pr} = -(n - \frac {m+k}{2}-1) \cdot ln \Lambda \end{equation*}

Wobei n die Anzahl der Testpersonen, m die Anzahl der unabhängigen Variablen und k die Anzahl der Gruppen darstellt. Für die Durchführung des Tests vergleichst Du \chi^2_{pr} mit \chi^2_{kr} bei (m\cdot (k-1)) Freiheitsgraden.
Den kanonische Korrelationskoeffizienten CR als Maß für die Stärke der Beziehungen erhältst Du als

    \begin{equation*} CR = \sqrt{1-\Lambda}, \quad CR^2 = 1-\Lambda \end{equation*}

Sein Quadrat, das kanonische Bestimmtheitsmaß, gibt den Streuungsanteil der Diskriminanzwerte an, der durch die Gruppenzugehörigkeit erklärt wird.