Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Conjoint-Analyse
- 26. April 2018
- Posted by: Mika
Ausgangspunkt der Conjoint-Anlalyse ist das Problem, dass Personen Objekte in ihrer Gesamtheit sehr wohl beurteilen können, meist aber nicht angeben können, in welchem Maße die verschiedenen Eigenschaften der Objekte zu ihrer Entscheidungsfindung beitragen, im Extremfall betrachten sie sie als „Bauchentscheidung“. Für das Design neuer Produkte beispielsweise ist es aber extrem wichtig zu wissen, welche Eigenschaften für die potentiellen Käufer relevant sind und welche Ausprägung der Eigenschaften den besten Markterfolg verspricht.
Aus erhobenen Präferenzrangfolgen zu einer Reihe von Objekten, die den Probanden mit Nennung ihrer Eigenschaften gezeigt wurden, bestimmt die Conjoint-Analyse die Nutzenanteile, die die verschiedenen Eigenschaften stiften, und ihre Bedeutung für die Entscheidungsfindung.
Damit kann dieses multivariate Verfahren etwa in der Marktforschung angewendet werden, um
- die Wichtigkeit der verschiedenen Eigenschaften beim Käufer zu ermitteln,
- zu erfahren, welche Bedeutung der Preis für den Kunden hat,
- welchen Aufpreis er für eine bestimmte Eigenschaft zu zahlen bereit wäre
- etc.
Das Verfahren ist auch unter den Namen Conjoint Measurement, Conjoint Methode oder Verbundmessung bekannt. „Conjoint“ ist eine Kurzfassung von „considered jointly“, was auf die Modellkonstruktion hinweist:
K zu beurteilende Objekte (Stimuli) werden als „Bündel“ oder „Komposition“ ihrer I Eigenschaften mit ![]() Ausprägungen betrachtet, aus denen der Nutzen
Ausprägungen betrachtet, aus denen der Nutzen ![]() des k-ten Objektes als Linearkombination entsteht:
des k-ten Objektes als Linearkombination entsteht:
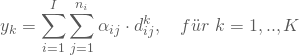
![]() ist der Nutzenwert, den die j-te Ausprägung der i-ten Eigenschaft stiftet.
ist der Nutzenwert, den die j-te Ausprägung der i-ten Eigenschaft stiftet. ![]() ist eine Dummyvariable, die den Wert Eins annimmt, falls die j-te Ausprägung der i-ten Eigenschaft bei dem betrachteten Objekt vorhanden ist; anderenfalls ist
ist eine Dummyvariable, die den Wert Eins annimmt, falls die j-te Ausprägung der i-ten Eigenschaft bei dem betrachteten Objekt vorhanden ist; anderenfalls ist ![]() gleich Null.
gleich Null.
Du erhebst nun von Deinen Probanden eine Rangfolge der zu beurteilenden Objekte. Daraus schätzt Du die Koeffizienten ![]() mittels der Methode der kleinsten Quadrate, so dass die Summe der quadratischen Abweichungen zwischen den erhobenen Rangwerten
mittels der Methode der kleinsten Quadrate, so dass die Summe der quadratischen Abweichungen zwischen den erhobenen Rangwerten ![]() und den geschätzten Nutzenwerten der Objekte
und den geschätzten Nutzenwerten der Objekte ![]() möglichst klein wird:
möglichst klein wird:
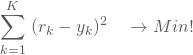
Dabei wird vereinfachend angenommen, die Präferenzurteile seien metrisch skaliert.
Stell Dir vor, Du konzipierst ein neues Navigationssystem und überlegst, welche Eigenschaften dieses haben soll. Bezüglich der folgenden Merkmale bist du noch unsicher:
| Eigenschaft | mögliche Ausprägungen | |||
| j i | 1 | 2 | 3 | |
| Bildschirmgröße | 1 | 5 Zoll | 6 Zoll | 7 Zoll |
| Bildschirmoberfläche | 2 | hochglänzend | matt | |
| Radarwarnung | 3 | ja | nein | |
Du kombinierst jetzt jede mögliche Ausprägung jeder Eigenschaft miteinander und erhältst ![]() Objekte mit unterschiedlichen Merkmalsausprägungen. Diese bietest Du den Probanden an, um deren Rangwertung zu erhalten. Die letzte Spalte der Tabelle zeigt die Rangordnung einer Person an; die Spalten
Objekte mit unterschiedlichen Merkmalsausprägungen. Diese bietest Du den Probanden an, um deren Rangwertung zu erhalten. Die letzte Spalte der Tabelle zeigt die Rangordnung einer Person an; die Spalten ![]() bis
bis ![]() enthalten die Werte der Dummies für die Zerlegung der Nutzenwerte.
enthalten die Werte der Dummies für die Zerlegung der Nutzenwerte.
| k | Eigenschaftskombinationen | Bildschirmgröße | Oberfläche | Radar | Rangwert des k-ten Objektes aus Sicht einer Testperson |
||||||
| 1 | 5 Zoll | hochglänzend | mit Radar | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 8 |
| 2 | ohne Radar | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | ||
| 3 | matt | mit Radar | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 6 | |
| 4 | ohne Radar | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 2 | ||
| 5 | 6 Zoll | hochglänzend | mit Radar | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 12 |
| 6 | ohne Radar | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 7 | ||
| 7 | matt | mit Radar | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 11 | |
| 8 | ohne Radar | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 5 | ||
| 9 | 7 Zoll | hochglänzend | mit Radar | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 10 |
| 10 | ohne Radar | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 3 | ||
| 11 | matt | mit Radar | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 9 | |
| 12 | ohne Radar | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | ||
Du regressierst jetzt mittels der Methode der kleinsten Quadrate die Rangwerte ![]() des Probanden als abhängige Variable auf die (unabhängigen) Dummies
des Probanden als abhängige Variable auf die (unabhängigen) Dummies ![]() und erhältst individuelle Schätzwerte für die zugehörigen Koeffizienten
und erhältst individuelle Schätzwerte für die zugehörigen Koeffizienten ![]() in der zweiten Tabellenspalte, die den zu i und j gehörigen Nutzenbeitrag darstellen.
in der zweiten Tabellenspalte, die den zu i und j gehörigen Nutzenbeitrag darstellen.
|
Koeffizient
|
individuelle Schätzwerte aus der Regression |
„verschobene“ Schätzwerte / Nutzenwerte |
Nutzenbeitrag jeder Eigenschaft am Gesamtnutzen |
|
|
– 2,25 | 0 | 0,00% |
|
|
2,25 | 2,25 | 41,51% |
|
|
– | 4,5 | 20,76% |
|
|
4,00 | 0,67 | 6,18% |
|
|
3,33 | 0 | 0,03% |
|
|
5,67 | 5,67 | 52,31% |
|
|
– | 0 | 0,00% |
| Summe der maximalen Nutzenwerte jeder Eigenschaft |
4,5+0,67+5,67 =10,84 |
||
Um die Koeffizienten interpersonell vergleichbar und über die Probanden aggregierbar zu machen, führst Du zwei Schritte durch:
- Zunächst verschiebst Du die Koeffizienten, die die Ausprägungen einer Eigenschaft erhalten haben, so auf der Zahlenskala, so dass der kleinste Koeffizient Null beträgt:
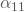 bis
bis 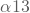 sind beispielsweise die Koeffizienten, die die Bildschirmgröße betreffen; die zugehörigen Schätzwerte aus der Regression lauten (-2,25;2,25;0). Der kleinste Koeffizient ist (-2,25): Du addierst daher zu allen Koeffizienten 2,25 hinzu und erhältst nach der Verschiebung die neuen Koeffizienten (0;2,25;4,5). Diese verschobenen Schätzwerte enthält die dritte Spalte der Tabelle.
sind beispielsweise die Koeffizienten, die die Bildschirmgröße betreffen; die zugehörigen Schätzwerte aus der Regression lauten (-2,25;2,25;0). Der kleinste Koeffizient ist (-2,25): Du addierst daher zu allen Koeffizienten 2,25 hinzu und erhältst nach der Verschiebung die neuen Koeffizienten (0;2,25;4,5). Diese verschobenen Schätzwerte enthält die dritte Spalte der Tabelle. - Danach berechnest Du die Summe der je Eigenschaft höchstens zu erreichenden Nutzenwerte zum maximal erreichbaren Gesamtnutzen: Hier beträgt der durch die Bildschirmgröße höchstens erreichte Nutzen 4,5; durch die Oberfläche wird maximal 0,67 und durch die Integration von Radarwarnungen maximal 5,67 erzielt; insgesamt kann also höchstens einen Nutzen von 10,84 erreicht werden.Den Nutzenbeitrag jeder Eigenschaftsausprägung am Gesamtnutzen kannst Du dann durch Division der verschobenen Schätzwerte durch die Summe der maximalen Nutzenwerte berechnen; diese Werte zeigt die letzte Spalte der Tabelle: So trägt etwa das Vorhandensein einer Radarwarnsystems mit 5,57 von maximal 10,84 Nutzeneinheiten zu
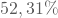 zum Gesamtnutzen bei.
zum Gesamtnutzen bei.
Aus diesen normierten individuellen Nutzenbeiträgen jeder Eigenschaft berechnest Du anschließend einen mittleren Gesamtnutzenbeitrag, wobei jeder Proband in der Regel die gleiche Gewichtung erhält.
Die erste Grafik zeigt – hier für den Fall eines einzigen Probanden – den maximalen Nutzenbeitrag jeder Eigenschaft und damit auch ihre Bedeutung für die Entscheidungsfindung. Je größer die Bedeutung einer Eigenschaft ist, umso wichtiger ist es, hier nach der Analyse die geeignete Ausprägung auszuwählen.
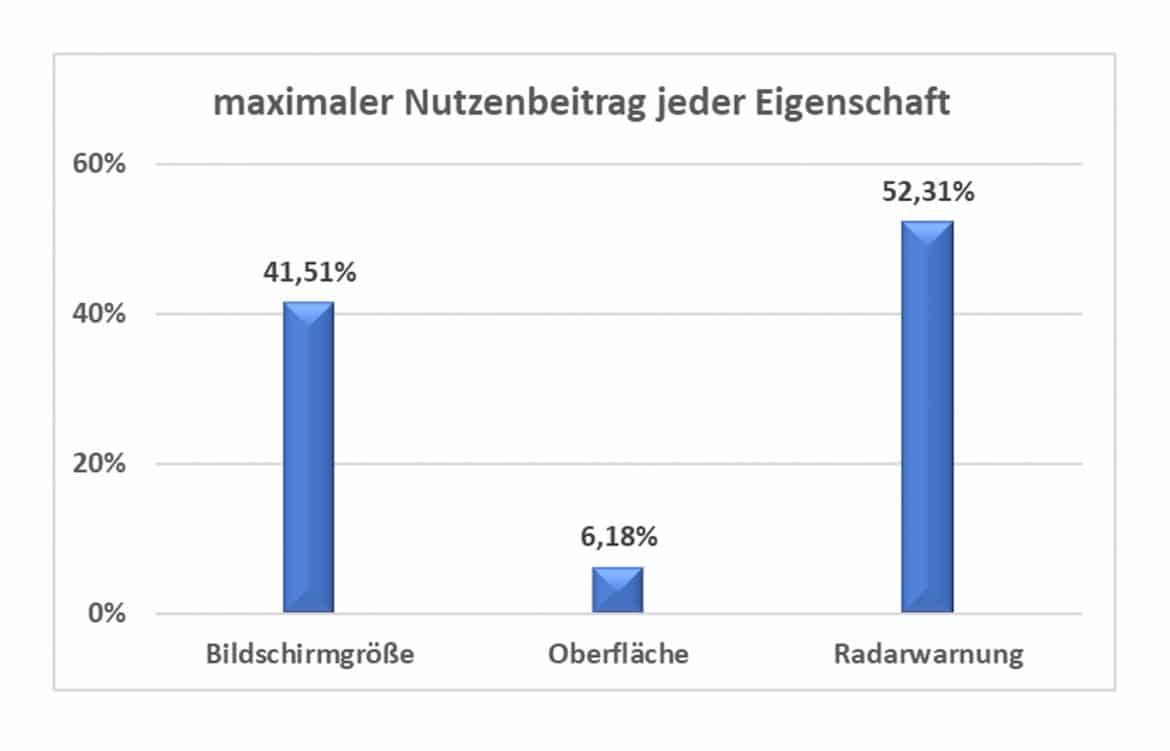
Der höchste Nutzenbeitrag ist hier beim Koeffizienten ![]() zu erkennen: wenn das Navigationsgerät Radarwarnungen vor Blitzern anbietet, beträgt der Beitrag dieser Eigenschaft zum Gesamtnutzen
zu erkennen: wenn das Navigationsgerät Radarwarnungen vor Blitzern anbietet, beträgt der Beitrag dieser Eigenschaft zum Gesamtnutzen ![]() .
.
Die Bildschirmgröße trägt höchstens ![]() zum Gesamtnutzen bei, wenn die hier optimale Bildschirmdiagonale von 6 Zoll vorliegt.
zum Gesamtnutzen bei, wenn die hier optimale Bildschirmdiagonale von 6 Zoll vorliegt.
Die Eigenschaft Bildschirmoberfläche bestimmt den Nutzenwert höchstens mit ![]() ; sie kann also am ehesten vernachlässigt werden.
; sie kann also am ehesten vernachlässigt werden.
Die nächste Grafik stellt die Nutzenbeiträge aller Eigenschaftsausprägungen gegenüber.
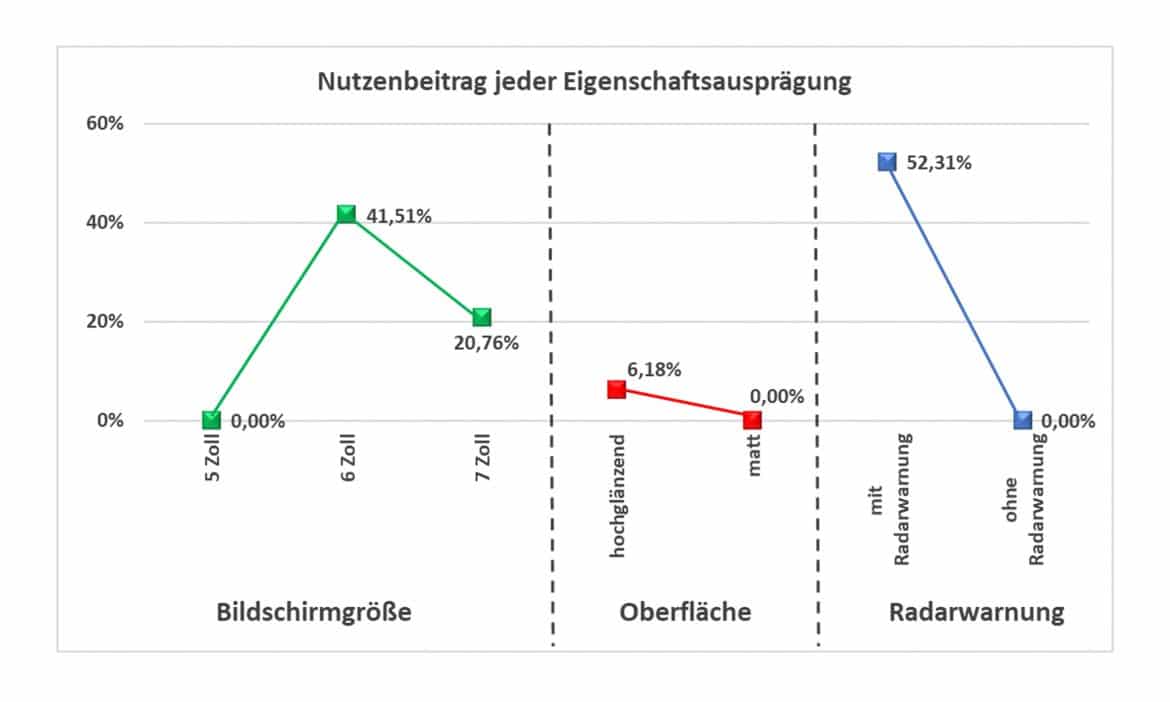
Vor der Durchführung einer Conjoint-Analyse solltest Du gut überlegen, welche Eigenschaften Deiner Objekte Du für die Bewertung verwendest: Sie sollten für die Entscheidung des Probanden relevant, unabhängig voneinander und nicht zu zahlreich sein, da sonst die Anzahl der zu beurteilenden Merkmalskombinationen schnell zu groß wird.
In der Praxis geht man davon aus, dass Probanden nicht mehr als 20 Objekte zuverlässig zu beurteilen vermögen. Mit mehreren Eigenschaften und deren Ausprägungen wird diese Zahl sehr schnell überschritten und ein vollständiges Design, d.h. jeder Proband beurteilt alle Objekte, ist dann nicht mehr möglich.
Du kannst dann entweder
- auf ein unvollständiges Design bei der Versuchsanordnung wechseln, bei dem nicht mehr jeder Proband alle Merkmalskombinationen beurteilen soll, oder
- auf alternative Befragungsmethoden zurückgreifen, aus denen dann die Präferenzrangfolgen abgeleitet werden können: Du kannst beispielsweise Ratingskalen oder paarweise Vergleiche einsetzen.
